51nod - 1537 分解

最新推荐文章于 2018-11-02 20:32:59 发布

brucehb

最新推荐文章于 2018-11-02 20:32:59 发布

阅读量203

点赞数

分类专栏：快速幂

本文链接：https://blog.youkuaiyun.com/brucehb/article/details/79843383

版权

快速幂专栏收录该内容

7 篇文章

订阅专栏

本文介绍了一种利用矩阵快速幂的方法来解决特定形式的数学表达式问题。对于给定的大整数n，文章详细阐述了如何判断并求解(1+√2)^n是否能被表示为√m+√(m-1)的形式，并给出了具体的C++实现代码。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

问(1+sqrt(2)) ^n 能否分解成 sqrt(m) +sqrt(m-1)的形式

如果可以输出 m%1e9+7 否则输出no

Input

一行，一个数n。（n<=10^18）

Output

一行，如果不存在m输出no，否则输出m%1e9+7

Input示例

Output示例

思路：

假设 $(1+\sqrt{2})^k = a + b \sqrt{2}$

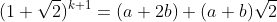
则： $(1+\sqrt{2})^{k+1} = (a + 2b) + (a + b)\sqrt{2}$

因此可以用矩阵快速幂的方式来计算出a和b的值。并且：当k为偶数时，m = a^2，当k为奇数时，m = 2*b^2 = a^2 + 1。

参考：https://blog.youkuaiyun.com/qingshui23/article/details/52350523

#include<iostream>  
#include<algorithm>  
#include<cstring>  
using namespace std;  
  
typedef long long ll;  
ll N = 2;  
const ll M = 1e9 + 7;  
  
struct Node  
{  
    ll a[2][2];  
};  
  
Node mul(Node a, Node b)  
{  
    Node result;  
    memset(result.a, 0, sizeof(result.a));  
    for(int i = 0; i < N; i++)
    {
        for(int j = 0; j < N;j++)  
        {
            for(int k = 0; k < N;++k)  
            {  
                result.a[i][j] += (a.a[i][k] * b.a[k][j]) % M;  
                result.a[i][j] %= M;  
            }  
        }
    }
    return result;  
}  
  
Node q_pow(Node a, ll n)  
{  
    Node b = a;  
    while (n > 0)  
    {  
        if (n & 1) 
        {
            b = mul(a, b);  
        }
        a = mul(a, a);  
        n >>= 1;  
    }  
    return b;  
}  
  
int main()  
{  
    ll n;  
    Node a;  
    cin >> n;
    for (int i = 0; i < N; ++i)  
    {
        for (int j = 0; j < N; ++j)  
        {
            a.a[i][j]=1;  
        }
    }
    a.a[0][1] = 2;  
    a = q_pow(a, n-1);  
    ll result = a.a[0][0] * a.a[0][0];  
    if (n & 1)
    {
        result++;  
    }
    result %= M;  
    cout << result << endl;  
    
    return 0;  
}