Denoising Diffusion Probabilistic Models (DDPM) 论文学习记录

Denoising Diffusion Probabilistic Models (DDPM)

1. 标题与摘要

1.1 核心信息

• 标题：去噪扩散概率模型
• 作者：Jonathan Ho, Ajay Jain, Pieter Abbeel (UC Berkeley)
• 代码：https://github.com/hojonathanho/diffusion

1.2 核心贡献

1. 理论创新：
   • 建立扩散模型与去噪得分匹配（Denoising Score Matching）和Langevin动力学的等价性。
   • 提出加权变分下界目标函数（§3.4）。
2. 性能突破：
   • CIFAR10：Inception Score 9.46，FID 3.17（无条件生成SOTA）。
   • 256×256 LSUN：样本质量媲美ProgressiveGAN。
3. 新视角：
   • 扩散采样过程可解释为渐进有损解压（Progressive Lossy Decompression），泛化自回归解码。

---

2. 引言

2.1 生成模型背景

• 现有模型（GANs/VAEs/自回归/流模型）在图像合成上取得进展，但扩散模型此前未证明能生成高质量样本。

2.2 扩散模型定义

• 前向过程（扩散过程）：
  $$q({\mathbf{x}}_{1:T}|{\mathbf{x}}_0):=\prod _{t=1}^T\mathcal{N}({\mathbf{x}}_t;\sqrt{1-{\beta }_t}{\mathbf{x}}_{t-1},{\beta }_t\mathbf{I})$$
  逐步添加高斯噪声（方差表 ${\beta }_{1:T}$ 固定或可学）。
• 反向过程：
  $$p_{\theta }({\mathbf{x}}_{0:T}):=p({\mathbf{x}}_T)\prod _{t=1}^T\mathcal{N}({\mathbf{x}}_{t-1};{\mathbf{\mu }}_{\theta }({\mathbf{x}}_t,t),{\Sigma }_{\theta }({\mathbf{x}}_t,t))$$
  学习从噪声重建数据的马尔可夫链。

2.3 本文贡献

• 首次证明扩散模型可生成高质量样本（优于部分已有模型）。
• 关键发现：通过 $ϵ$-预测参数化，建立与去噪得分匹配的显式联系（§3.2）。

---

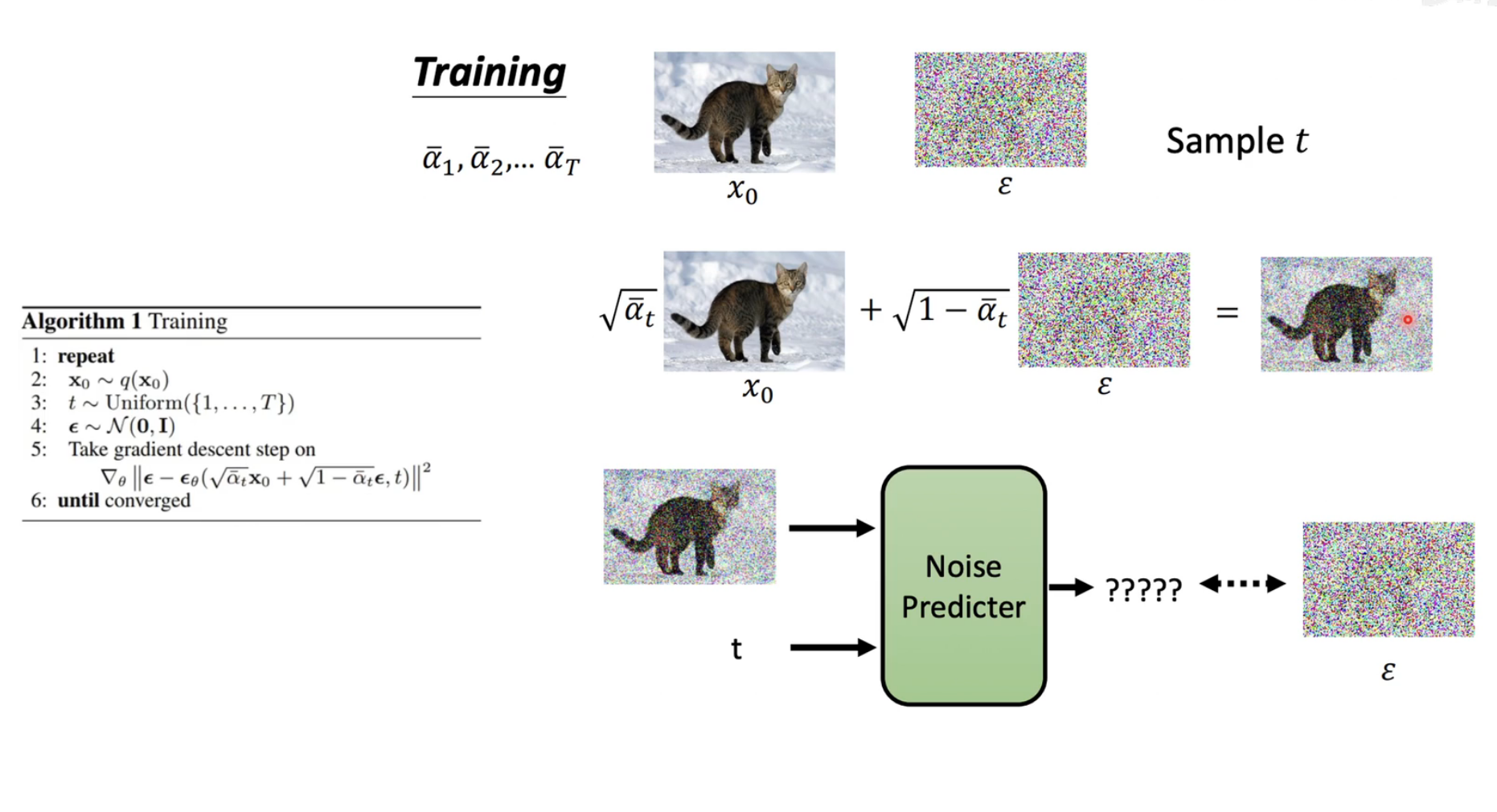
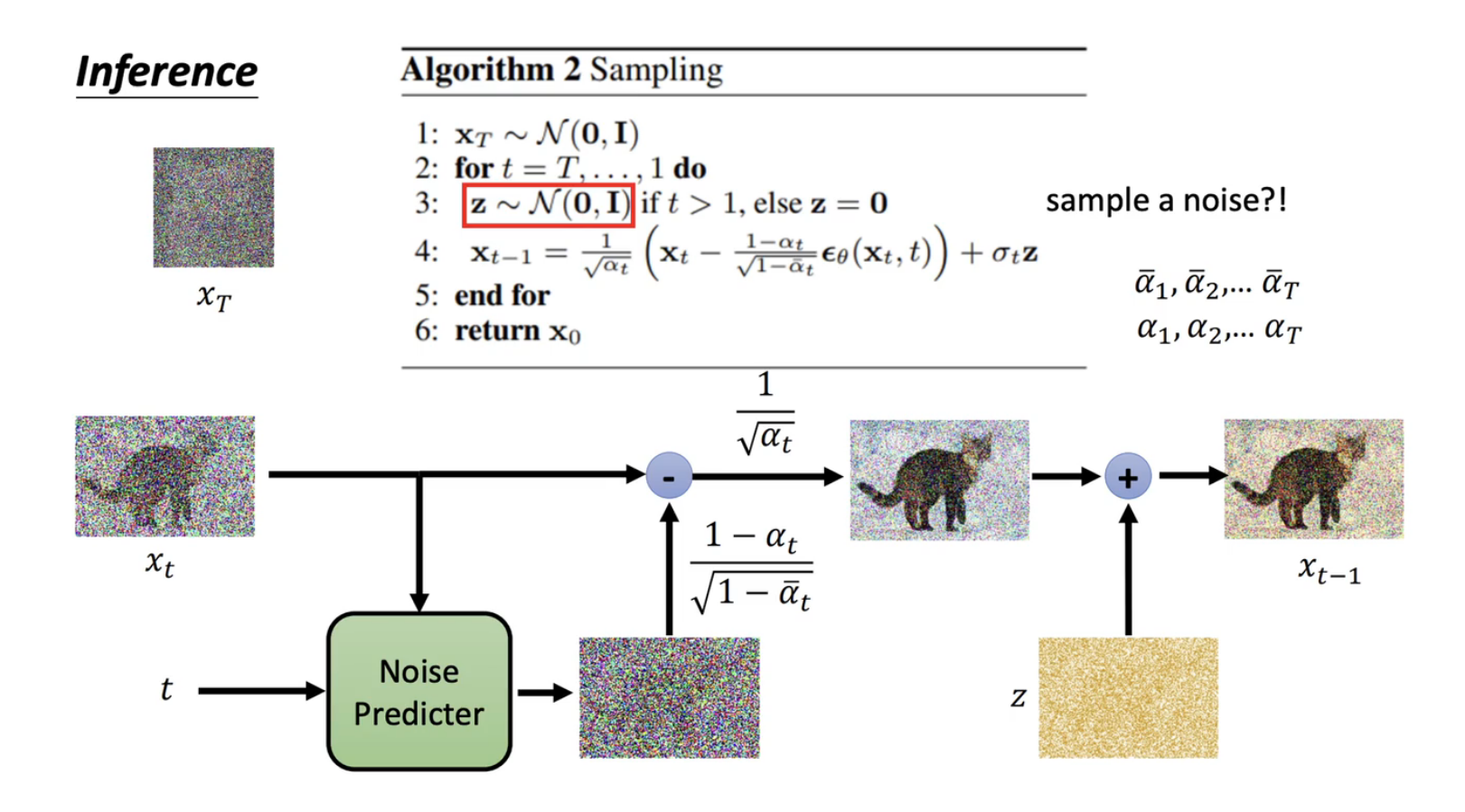
3. 背景

公式解析

3.1 数学框架

符号	定义
${\mathbf{x}}_0$	原始数据
${\mathbf{x}}_{1:T}$	隐变量（同维噪声）
$q({\mathbf{x}}_t|{\mathbf{x}}_{t-1})$	前向转移（加噪）
$p_{\theta }({\mathbf{x}}_{t-1}|{\mathbf{x}}_t)$	反向转移（去噪）

3.2 训练目标

优化变分下界（ELBO）：
$$\mathbb{E}[-\log p_{\theta }({\mathbf{x}}_0)]\le {\mathbb{E}}_q\left[-\log \frac{p_{\theta }({\mathbf{x}}_{0:T})}{q({\mathbf{x}}_{1:T}|{\mathbf{x}}_0)}\right]=:L$$
方差缩减形式：
$$L={\mathbb{E}}_q\left[\underset{L_T}{\underbrace{D_{\text{KL}}(q({\mathbf{x}}_T|{\mathbf{x}}_0)\parallel p({\mathbf{x}}_T))}}+\sum _{t>1}\underset{L_{t-1}}{\underbrace{D_{\text{KL}}(q({\mathbf{x}}_{t-1}|{\mathbf{x}}_t,{\mathbf{x}}_0)\parallel p_{\theta }({\mathbf{x}}_{t-1}|{\mathbf{x}}_t))}}-\underset{L_0}{\underbrace{\log p_{\theta }({\mathbf{x}}_0|{\mathbf{x}}_1)}}\right]$$

3.3 闭式性质

前向过程任意步采样：
$$q({\mathbf{x}}_t|{\mathbf{x}}_0)=\mathcal{N}({\mathbf{x}}_t;\sqrt{{\bar{\alpha }}_t}{\mathbf{x}}_0,(1-{\bar{\alpha }}_t)\mathbf{I})$$
其中 ${\alpha }_t:=1-{\beta }_t$, ${\bar{\alpha }}_t:={\prod }_{s=1}^t{\alpha }_s$。

---

4. 扩散模型与去噪自编码器

这一部分是整篇论文的核心，它建立了扩散模型与去噪分数匹配之间的深刻联系，并由此引出了简化且高效的训练目标。本章旨在为扩散模型的具体实现做出设计和论证。作者回答了三个关键问题：

1. 前向过程的方差 ${\beta }_t$ 应该如何设定？（对应 $L_T$）
2. 反向过程（模型） 应该如何参数化和训练？（对应 $L_{1:T-1}$）
3. 如何计算最终的数据对数似然？（对应 $L_0$）

---

4.1 Forward process and $L_T$ （前向过程与 $L_T$）

• 内容：作者选择将前向过程的方差 ${\beta }_t$ 固定为常数，而不是作为可学习的参数。
• 原因：
  1. 简化问题：前向过程 $q$ 因此不再包含任何可学习参数，成为一个固定的（预定义的）噪声添加过程。
  2. $L_T$ 成为常数：损失函数中的 $L_T=D_{KL}(q(x_T|x_0)\Vert p(x_T))$ 衡量的是前向过程最终分布与先验分布（标准高斯分布）的差异。由于 $q$ 和 $p$ 都是固定的高斯分布，它们的KL散度是一个可以预先计算的常数，在训练过程中不需要优化，可以忽略。
• 实践意义：这大大简化了训练过程，我们只需要关注反向过程的训练 ($L_0$ 到 $L_{T-1}$)。

---

4.2 Reverse process and $L_{1:T-1}$ （反向过程与 L 1 : T − 1 L_{1:T-1}