《Attention Is All You Need》论文学习记录
摘要(Abstract)
- 核心贡献:提出Transformer架构,完全基于注意力机制,摒弃循环(RNN/LSTM)和卷积(CNN)结构。
- 核心优势:
- 更强的并行性(more parallelizable)
- 显著减少训练时间(less time to train)
- 实验结果:
- WMT 2014 英德翻译:28.4 BLEU(超越当时SOTA 2 BLEU以上)
- WMT 2014 英法翻译:41.8 BLEU(单模型SOTA,8 GPU训练3.5天)
- 泛化能力:在英语选区解析任务中表现优异(有限/大数据场景均有效)
1 引言(Introduction)
- 传统模型局限:
- RNN/LSTM/GRU主导序列建模,但顺序计算阻碍并行化,长序列处理效率低。
- 注意力机制常与RNN耦合使用(如Seq2Seq+Attention)。
- Transformer创新:
- 纯注意力架构:直接建模输入输出的全局依赖关系。
- 计算效率:8 P100 GPU训练12小时即可达到SOTA翻译质量。
2 背景(Background)
- 并行化尝试:
- 卷积模型(如ByteNet, ConvS2S)可并行计算,但长距离依赖学习困难(计算复杂度随距离增长)。
- 自注意力(Self-Attention):
- 用于单序列内部位置关系建模(如阅读理解、摘要生成)。
- Transformer定位:
- 首个完全依赖自注意力的序列转导模型,无需RNN/CNN。
3 模型架构(Model Architecture)
3.1 整体结构
- Encoder-Decoder框架:
- Encoder:将输入序列映射为连续表示 z = ( z 1 , . . . , z n ) \mathbf{z} = (z_1,...,z_n) z=(z1,...,zn)
- Decoder:自回归生成输出序列 ( y 1 , . . . , y m ) (y_1,...,y_m) (y1,...,ym),使用 z \mathbf{z} z 及历史输出。
- 核心组件:
- 堆叠自注意力层 + 逐位置全连接前馈网络(Figure 1)。

- 堆叠自注意力层 + 逐位置全连接前馈网络(Figure 1)。
3.2 编码器与解码器栈
| 组件 | 结构细节 |
|---|---|
| Encoder |
N
=
6
N=6
N=6 个相同层 每层含 多头自注意力子层 + 前馈网络子层 每子层后接 残差连接 + 层归一化: LayerNorm(x + Sublayer(x)) 输出维度 d model = 512 d_{\text{model}}=512 dmodel=512 |
| Decoder |
N
=
6
N=6
N=6 个相同层 额外插入 编码器-解码器注意力子层(Query来自解码器,Key/Value来自编码器) 自注意力子层使用掩码:禁止位置 i i i关注 > i >i >i的未来位置 |
3.3 注意力机制
3.3.1 缩放点积注意力(Scaled Dot-Product Attention)

- 计算流程:
Attention ( Q , K , V ) = softmax ( Q K T d k ) V \text{Attention}(Q,K,V) = \text{softmax}\left(\frac{QK^T}{\sqrt{d_k}}\right)V Attention(Q,K,V)=softmax(dkQKT)V - 缩放因子
1
d
k
\frac{1}{\sqrt{d_k}}
dk1 的作用:
- 当 d k d_k dk 较大时,点积值过大导致softmax梯度极小。
- 缩放控制方差为1,稳定训练。
原文所述:
To illustrate why the dot products get large, assume that the components of q q q and k k k are independent random variables with mean 0 and variance 1. Then their dot product, q ⋅ k = ∑ i = 1 d k q i k i q \cdot k = \sum_{i=1}^{d_k} q_i k_i q⋅k=∑i=1dkqiki, has mean 0 and variance d k d_k dk.
3.3.1.1 点积的均值和方差推导
-
假设:向量 q q q 和 k k k 的每个分量是独立的随机变量,且每个分量的均值为 0,方差为 1。
- q = [ q 1 , q 2 , … , q d k ] q = [q_1, q_2, \dots, q_{d_k}] q=[q1,q2,…,qdk]
- k = [ k 1 , k 2 , … , k d k ] k = [k_1, k_2, \dots, k_{d_k}] k=[k1,k2,…,kdk]
- E [ q i ] = 0 \mathbb{E}[q_i] = 0 E[qi]=0
- E [ k i ] = 0 \mathbb{E}[k_i] = 0 E[ki]=0
- Var ( q i ) = 1 \text{Var}(q_i) = 1 Var(qi)=1
- Var ( k i ) = 1 \text{Var}(k_i) = 1 Var(ki)=1
-
点积公式:
q ⋅ k = ∑ i = 1 d k q i k i q \cdot k = \sum_{i=1}^{d_k} q_i k_i q⋅k=i=1∑dkqiki
其中, d k d_k dk 是向量的维度。 -
均值计算:
E [ q ⋅ k ] = E [ ∑ i = 1 d k q i k i ] \mathbb{E}[q \cdot k] = \mathbb{E}\left[\sum_{i=1}^{d_k} q_i k_i\right] E[q⋅k]=E[i=1∑dkqiki]
由于 q i q_i qi 和 k i k_i ki 是独立的随机变量,且均值为 0:
E [ q i k i ] = E [ q i ] ⋅ E [ k i ] = 0 ⋅ 0 = 0 \mathbb{E}[q_i k_i] = \mathbb{E}[q_i] \cdot \mathbb{E}[k_i] = 0 \cdot 0 = 0 E[qiki]=E[qi]⋅E[ki]=0⋅0=0
因此:
E [ q ⋅ k ] = ∑ i = 1 d k E [ q i k i ] = ∑ i = 1 d k 0 = 0 \mathbb{E}[q \cdot k] = \sum_{i=1}^{d_k} \mathbb{E}[q_i k_i] = \sum_{i=1}^{d_k} 0 = 0 E[q⋅k]=i=1∑dkE[qiki]=i=1∑dk0=0
所以,点积 q ⋅ k q \cdot k q⋅k 的均值为 0。 -
方差计算:
Var ( q ⋅ k ) = Var ( ∑ i = 1 d k q i k i ) \text{Var}(q \cdot k) = \text{Var}\left(\sum_{i=1}^{d_k} q_i k_i\right) Var(q⋅k)=Var(i=1∑dkqiki)
由于 q i q_i qi 和 k i k_i ki 是独立的随机变量,且方差为 1:
Var ( q i k i ) = E [ ( q i k i ) 2 ] − ( E [ q i k i ] ) 2 Var ( q i k i ) = E [ ( q i k i ) 2 ] \text{Var}(q_i k_i) = \mathbb{E}[(q_i k_i)^2] - (\mathbb{E}[q_i k_i])^2 \\[10pt] \text{Var}(q_i k_i) = \mathbb{E}[(q_i k_i)^2] Var(qiki)=E[(qiki)2]−(E[qiki])2Var(qiki)=E[(qiki)2]
由于 q i q_i qi 和 k i k_i ki 是独立的:
E [ ( q i k i ) 2 ] = E [ q i 2 ] ⋅ E [ k i 2 ] \mathbb{E}[(q_i k_i)^2] = \mathbb{E}[q_i^2] \cdot \mathbb{E}[k_i^2] E[(qiki)2]=E[qi2]⋅E[ki2]
由于 Var ( q i ) = 1 \text{Var}(q_i) = 1 Var(qi)=1 和 Var ( k i ) = 1 \text{Var}(k_i) = 1 Var(ki)=1:
E [ q i 2 ] = Var ( q i ) + ( E [ q i ] ) 2 = 1 + 0 = 1 E [ k i 2 ] = Var ( k i ) + ( E [ k i ] ) 2 = 1 + 0 = 1 \mathbb{E}[q_i^2] = \text{Var}(q_i) + (\mathbb{E}[q_i])^2 = 1 + 0 = 1 \\[10pt] \mathbb{E}[k_i^2] = \text{Var}(k_i) + (\mathbb{E}[k_i])^2 = 1 + 0 = 1 E[qi2]=Var(qi)+(E[qi])2=1+0=1E[ki2]=Var(ki)+(E[ki])2=1+0=1
因此:
E [ ( q i k i ) 2 ] = 1 ⋅ 1 = 1 \mathbb{E}[(q_i k_i)^2] = 1 \cdot 1 = 1 E[(qiki)2]=1⋅1=1
所以:
Var ( q i k i ) = 1 \text{Var}(q_i k_i) = 1 Var(qiki)=1
由于 q i k i q_i k_i qiki 是独立的:
Var ( q ⋅ k ) = ∑ i = 1 d k Var ( q i k i ) = ∑ i = 1 d k 1 = d k \text{Var}(q \cdot k) = \sum_{i=1}^{d_k} \text{Var}(q_i k_i) = \sum_{i=1}^{d_k} 1 = d_k Var(q⋅k)=i=1∑dkVar(qiki)=i=1∑dk1=dk
所以,点积 q ⋅ k q \cdot k q⋅k 的方差为 d k d_k dk。
这意味着,随着维度 d k d_k dk 的增加,点积 q ⋅ k q \cdot k q⋅k 的方差也会线性增加。因此,点积的值可能会变得非常大,尤其是在高维情况下。这在 Transformer 架构中是一个重要的考虑因素,因为点积的大小会影响注意力机制的计算,可能导致梯度爆炸等问题。
3.3.1.2 缩放后的方差推导
-
原始点积方差:
Var ( q ⋅ k ) = d k \text{Var}(q \cdot k) = d_k Var(q⋅k)=dk -
缩放后的点积:
s = q ⋅ k d k s = \frac{q \cdot k}{\sqrt{d_k}} s=dkq⋅k
根据方差性质 Var ( a X ) = a 2 Var ( X ) \text{Var}(aX) = a^2\text{Var}(X) Var(aX)=a2Var(X):
Var ( s ) = Var ( q ⋅ k d k ) = ( 1 d k ) 2 ⋅ Var ( q ⋅ k ) = 1 d k ⋅ d k = 1 \text{Var}(s) = \text{Var}\left(\frac{q \cdot k}{\sqrt{d_k}}\right) = \left(\frac{1}{\sqrt{d_k}}\right)^2 \cdot \text{Var}(q \cdot k) = \frac{1}{d_k} \cdot d_k = 1 Var(s)=Var(dkq⋅k)=(dk1)2⋅Var(q⋅k)=dk1⋅dk=1
结果:缩放后的方差 Var ( s ) = 1 \text{Var}(s) = 1 Var(s)=1,与维度 d k d_k dk 无关。
3.3.1.3 掩码机制
原文所述
解码器中的自注意力层允许解码器中的每个位置能够关注到该位置之前(包括该位置)的所有位置。为了保持自回归的特性,我们需要防止解码器中的信息向左流动。我们通过在缩放点积注意力中屏蔽(设置为 − ∞ -\infty −∞) s o f t m a x softmax softmax 输入中对应非法连接的所有值来实现这一点。
Python 伪代码
# 生成过程伪代码
output = [START] # 初始状态
for t in range(3): # 生成3个token
# 关键技巧:添加掩码占位符
input_seq = output + [MASK] * (3 - t)
# 解码器计算:看到的是占位符,不是真实内容!
hidden = decoder(input_seq)
# 只预测最后一个掩码位置
next_token = argmax(hidden[-1])
output.append(next_token)
| 步骤 | 输入序列 | 可见内容 | 预测输出 |
|---|---|---|---|
| 1 | [ < s t a r t > <start> <start>, MASK, MASK, MASK] | < s t a r t > <start> <start> + 位置1(MASK) | 我 |
| 2 | [ < s t a r t > <start> <start> , 我, MASK, MASK] | < s t a r t > <start> <start> + 我 + 位置2(MASK) | 爱 |
| 3 | [ < s t a r t > <start> <start>, 我, 爱, MASK] | < s t a r t > <start> <start> + 我 + 爱 + 位置3(MASK) | AI |

3.3.2 多头注意力(Multi-Head Attention)

- 设计动机:
- 单头注意力抑制不同表示子空间的信息捕获。
- 机制:
MultiHead ( Q , K , V ) = Concat ( head 1 , . . . , head h ) W O head i = Attention ( Q W i Q , K W i K , V W i V ) \begin{align*} \text{MultiHead}(Q,K,V) &= \text{Concat}(\text{head}_1,...,\text{head}_h)W^O \\ \text{head}_i &= \text{Attention}(QW_i^Q, KW_i^K, VW_i^V) \end{align*} MultiHead(Q,K,V)headi=Concat(head1,...,headh)WO=Attention(QWiQ,KWiK,VWiV)
其中,投影矩阵为参数矩阵 W i Q ∈ R d model × d k W_i^Q \in \mathbb{R}^{d_{\text{model}} \times d_k} WiQ∈Rdmodel×dk, W i K ∈ R d model × d k W_i^K \in \mathbb{R}^{d_{\text{model}} \times d_k} WiK∈Rdmodel×dk, W i V ∈ R d model × d v W_i^V \in \mathbb{R}^{d_{\text{model}} \times d_v} WiV∈Rdmodel×dv,以及 W O ∈ R h d v × d model W^O \in \mathbb{R}^{h d_v \times d_{\text{model}}} WO∈Rhdv×dmodel。
- 参数配置:
- h = 8 h=8 h=8 个头, d k = d v = d model / h = 64 d_k = d_v = d_{\text{model}}/h = 64 dk=dv=dmodel/h=64
- 总计算量与全维单头注意力相近。
原文所述:
Instead of performing a single attention function with d model d_{\text{model}} dmodel-dimensional keys, values and queries, we found it beneficial to linearly project the queries, keys and values h h htimes with different, learned linear projections to d k d_k dk, d k d_k dk and d v d_v dv dimensions, respectively. On each of these projected versions of queries, keys and values we then perform the attention function in parallel, yielding d v d_v dv-dimensional output values. These are concatenated and once again projected, resulting in the final values.
3.3.3 注意力在模型中的应用
| 注意力类型 | 作用机制 |
|---|---|
| Encoder Self-Attention | Key/Value/Query均来自同一输入序列,捕获序列内部依赖。 |
| Decoder Masked Self-Attention | Key/Value/Query来自解码器,掩码确保自回归性。 |
| Encoder-Decoder Attention | Query来自解码器,Key/Value来自编码器输出(类似传统Seq2Seq注意力)。 |
原文所述(Self-Attention):
The encoder contains self-attention layers. In a self-attention layer all of the keys, values and queries come from the same place, in this case, the output of the previous layer in the encoder. Each position in the encoder can attend to all positions in the previous layer of the encoder.
3.4 位置前馈网络(Position-wise FFN)
3.4.1 结构:
FFN ( x ) = max ( 0 , x W 1 + b 1 ) W 2 + b 2 \text{FFN}(x) = \max(0, xW_1 + b_1)W_2 + b_2 FFN(x)=max(0,xW1+b1)W2+b2
- 两层线性变换 + ReLU激活。
- 输入/输出维 d model = 512 d_{\text{model}}=512 dmodel=512,隐层维 d f f = 2048 d_{ff}=2048 dff=2048。
3.4.2 特点:
- 独立应用于每个位置,参数跨位置共享但跨层不同。
3.4.3 并行化实现机制
🔑并行计算伪代码
输入张量形状 = [batch_size, seq_len, d_model]
# 示例: [32, 100, 512] 表示32个样本,每个样本100个位置,每个位置512维
# 输入: [batch_size, seq_len, 512]
X_reshaped = reshape(X, [batch_size * seq_len, 512])
# 第一层并行计算 (所有位置同时)
H = ReLU(X_reshaped @ W₁ + b₁) # [batch_size*seq_len, 2048]
# 第二层并行计算
Y_reshaped = H @ W₂ + b₂ # [batch_size*seq_len, 512]
# 恢复原始形状
Y = reshape(Y_reshaped, [batch_size, seq_len, 512])
(W₁形状为[512,2048], W₂形状为[2048,512])
3.4.3.1 并行计算的本质:独立计算,结果共存
当 FFN 层并行处理序列中所有位置时(比如一个包含 N N N 个 token 的序列):
- 每个位置 i i i 的计算 F F N ( x i ) = W 2 ⋅ R e L U ( W 1 ⋅ x i + b 1 ) + b 2 FFN(x_i) = W_2 \cdot ReLU(W_1 \cdot x_i + b_1) + b_2 FFN(xi)=W2⋅ReLU(W1⋅xi+b1)+b2 是独立进行的。
- 但这 N N N 个独立的计算共享同一组参数 W 1 , b 1 , W 2 , b 2 W_1, b_1, W_2, b_2 W1,b1,W2,b2。
- 并行计算完成后,得到的是一个批量的输出 [ y 1 , y 2 , … , y N ] [y_1, y_2, \dots, y_N] [y1,y2,…,yN],每个 y i y_i yi 对应一个位置的输出。
3.4.3.2 损失函数:聚合所有位置的影响
模型的损失函数 L L L(如交叉熵损失)通常是基于整个序列的输出 [ y 1 , y 2 , … , y N ] [y_1, y_2, \dots, y_N] [y1,y2,…,yN] 和对应的目标序列计算出来的。
这意味着最终的损失 L L L 综合了所有位置 i i i 的输出 y i y_i yi 对目标的贡献(或误差)。
3.4.3.3 反向传播(梯度回传)的关键:链式法则与参数共享
当进行反向传播计算损失 L L L 对参数 θ \theta θ(例如 W 1 W_1 W1 中的一个权重 w w w)的梯度 ∂ L ∂ θ \frac{\partial L}{\partial \theta} ∂θ∂L 时,链式法则告诉我们:
∂ L ∂ θ = ∑ i = 1 N ( ∂ L ∂ y i ⋅ ∂ y i ∂ θ ) \frac{\partial L}{\partial \theta} = \sum_{i=1}^{N} \left( \frac{\partial L}{\partial y_i} \cdot \frac{\partial y_i}{\partial \theta} \right) ∂θ∂L=i=1∑N(∂yi∂L⋅∂θ∂yi)
这个求和公式 ∑ \sum ∑ 是理解并行梯度回传的核心!
解释:
- ∂ L ∂ y i \frac{\partial L}{\partial y_i} ∂yi∂L:损失 L L L 对特定位置 i i i 的输出 y i y_i yi 的梯度。这取决于损失函数如何定义(通常 L L L 是各位置损失之和)。
- ∂ y i ∂ θ \frac{\partial y_i}{\partial \theta} ∂θ∂yi:特定位置 i i i 的输出 y i y_i yi 对参数 θ \theta θ 的梯度。因为 y i y_i yi 是通过 θ \theta θ(即 W 1 , b 1 , W 2 , b 2 W_1, b_1, W_2, b_2 W1,b1,W2,b2)计算出来的,所以这个梯度只依赖于位置 i i i 的计算路径。
- 求和
∑
i
=
1
N
\sum_{i=1}^{N}
∑i=1N:由于参数
θ
\theta
θ 被所有位置共享,它对总损失
L
L
L 的影响是通过所有使用了它的位置的贡献累加起来的。总梯度
∂
L
∂
θ
\frac{\partial L}{\partial \theta}
∂θ∂L 是所有位置
i
i
i 的局部梯度
(
∂
L
∂
y
i
⋅
∂
y
i
∂
θ
)
\left( \frac{\partial L}{\partial y_i} \cdot \frac{\partial y_i}{\partial \theta} \right)
(∂yi∂L⋅∂θ∂yi) 的和。
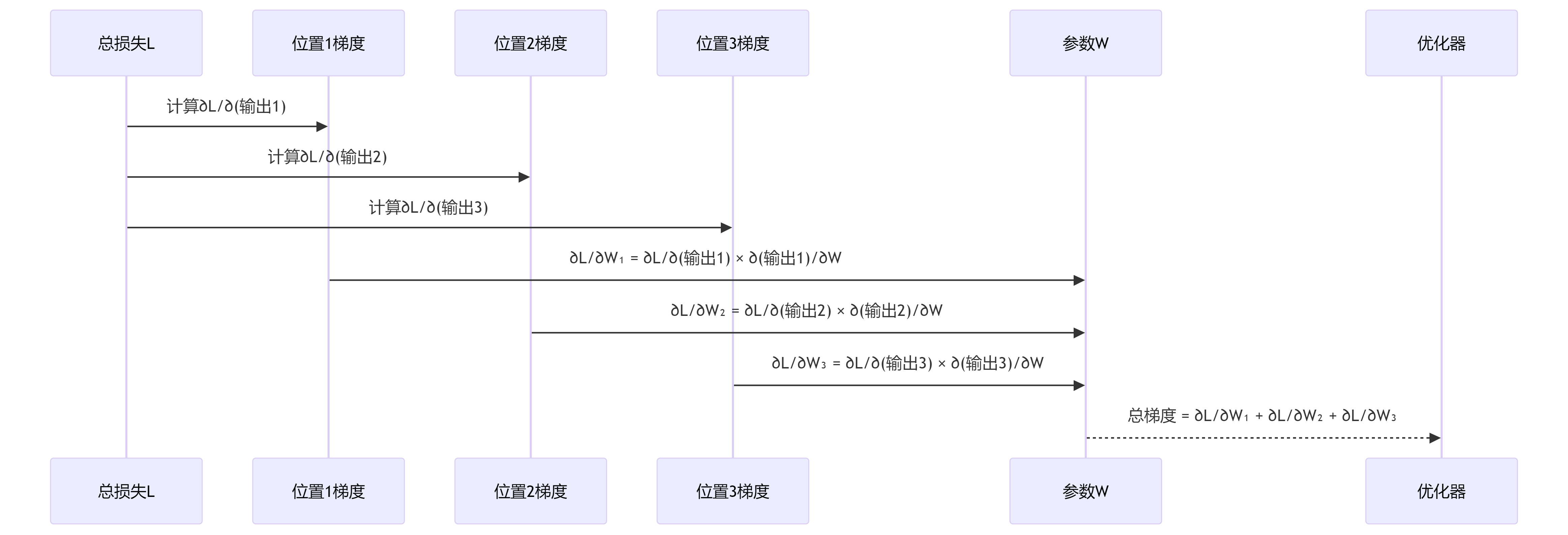
3.4.3.3 并行梯度计算的实现
自动微分框架的魔法
像 PyTorch 或 TensorFlow 这样的框架,在构建前向传播计算图时,会自动记录每个操作和依赖关系。
并行前向传播
当框架并行地计算出 [ y 1 , y 2 , … , y N ] [y_1, y_2, \dots, y_N] [y1,y2,…,yN] 时,它内部为每个位置 i i i 的计算都维护了独立的、局部的计算子图(虽然这些子图结构完全相同,共享参数)。
并行反向传播
-
计算损失对输出的梯度:
- 框架首先计算损失 L L L 对每个输出 y i y_i yi 的梯度 ∂ L ∂ y i \frac{\partial L}{\partial y_i} ∂yi∂L。
-
并行计算局部梯度:
- 然后,框架可以并行地计算每个位置 i i i 上, y i y_i yi 对参数 θ \theta θ 的局部梯度 ∂ y i ∂ θ \frac{\partial y_i}{\partial \theta} ∂θ∂yi。这一步利用了 GPU/TPU 强大的并行计算能力,同时对 N N N 个位置进行计算。
-
梯度聚合(Gradient Accumulation):
- 框架收集所有 N N N 个位置的局部梯度 ( ∂ L ∂ y i ⋅ ∂ y i ∂ θ ) \left( \frac{\partial L}{\partial y_i} \cdot \frac{\partial y_i}{\partial \theta} \right) (∂yi∂L⋅∂θ∂yi)。
- 关键一步来了:它将这些局部梯度累加(Sum)起来,得到参数
θ
\theta
θ 的总梯度:
∂ L ∂ θ = ∑ i = 1 N ( ∂ L ∂ y i ⋅ ∂ y i ∂ θ ) \frac{\partial L}{\partial \theta} = \sum_{i=1}^{N} \left( \frac{\partial L}{\partial y_i} \cdot \frac{\partial y_i}{\partial \theta} \right) ∂θ∂L=i=1∑N(∂yi∂L⋅∂θ∂yi)
这个累加操作也是高度优化的。
-
参数更新:
- 优化器(如 SGD, Adam)使用这个聚合后的总梯度 ∂ L ∂ θ \frac{\partial L}{\partial \theta} ∂θ∂L 来更新参数 θ \theta θ。参数 θ \theta θ 只被更新一次,使用的是所有位置贡献的总和。
原文所述:
In addition to attention sub-layers, each of the layers in our encoder and decoder contains a fully connected feed-forward network, which is applied to each position separately and identically. This consists of two linear transformations with a R e L U ReLU ReLU activation in between. While the linear transformations are the same across different positions, they use different parameters from layer to layer. Another way of describing this is as two convolutions with kernel size 1.The dimensionality of input and output is d model = 512 d_{\text{model}} = 512 dmodel=512, and the inner-layer has dimensionality d ff = 2048 d_{\text{ff}} = 2048 dff=2048.
3.5 嵌入与Softmax
- 共享权重:输入/输出嵌入层与Softmax前线性变换共享权重矩阵。
- 嵌入缩放:嵌入权重乘以 d model \sqrt{d_{\text{model}}} dmodel。
伪代码实现
import torch
import torch.nn as nn
import math
class TransformerWithSharedEmbeddings(nn.Module):
def __init__(self, vocab_size, d_model):
super().__init__()
self.d_model = d_model
self.vocab_size = vocab_size
# 共享的嵌入矩阵 - 关键点1:权重共享
self.shared_embedding = nn.Embedding(vocab_size, d_model)
# 解码器输出层(预softmax线性层)也共享同一个权重矩阵
# 注意:这里使用共享嵌入矩阵的转置作为线性层的权重
self.output_projection = nn.Linear(d_model, vocab_size, bias=False)
self.output_projection.weight = nn.Parameter(self.shared_embedding.weight.t())
# 其他组件(编码器、解码器、注意力等)
self.encoder = Encoder(d_model)
self.decoder = Decoder(d_model)
def forward(self, src_tokens, tgt_tokens):
# === 输入嵌入处理 ===
# 输入token -> 嵌入向量
src_emb = self.shared_embedding(src_tokens) # [batch, seq_len] -> [batch, seq_len, d_model]
# 关键点2:嵌入缩放
src_emb = src_emb * math.sqrt(self.d_model)
# === 输出嵌入处理(用于解码器输入)===
tgt_emb = self.shared_embedding(tgt_tokens) # 使用相同的权重矩阵
tgt_emb = tgt_emb * math.sqrt(self.d_model) # 同样进行缩放
# === 编码器-解码器处理 ===
memory = self.encoder(src_emb) # 编码器处理
decoder_output = self.decoder(tgt_emb, memory) # 解码器处理
# === 输出预测 ===
# 使用共享权重(嵌入矩阵的转置)进行线性变换
logits = self.output_projection(decoder_output) # [batch, seq_len, d_model] -> [batch, seq_len, vocab_size]
# Softmax得到概率分布
probs = torch.softmax(logits, dim=-1)
return probs
原文所述:
Similarly to other sequence transduction models, we use learned embeddings to convert the input tokens and output tokens to vectors of dimension d model d_{\text{model}} dmodel. We also use the usual learned linear transformation and softmax function to convert the decoder output to predicted next-token probabilities. In our model, we share the same weight matrix between the two embedding layers and the pre-softmax linear transformation, similar to [30]. In the embedding layers, we multiply those weights by d model \sqrt{d_{\text{model}}} dmodel.
[30] Using the Output Embedding to Improve Language Models
3.6 位置编码(Positional Encoding)
- 目的:为无循环/卷积的模型注入序列顺序信息。
- 公式:
P E ( p o s , 2 i ) = sin ( p o s / 10000 2 i / d model ) P E ( p o s , 2 i + 1 ) = cos ( p o s / 10000 2 i / d model ) \begin{align} PE_{(pos,2i)} &= \sin(pos / 10000^{2i/d_{\text{model}}}) \\ PE_{(pos,2i+1)} &= \cos(pos / 10000^{2i/d_{\text{model}}}) \end{align} PE(pos,2i)PE(pos,2i+1)=sin(pos/100002i/dmodel)=cos(pos/100002i/dmodel) - 优势:
- 可学习相对位置( P E p o s + k PE_{pos+k} PEpos+k 是 P E p o s PE_{pos} PEpos 的线性函数)。
- 支持外推到长于训练时的序列。
4 自注意力的优势(Why Self-Attention)
理论对比
| 层类型 | 计算复杂度 | 顺序操作数 | 最大路径长 |
|---|---|---|---|
| Self-Attention | O ( n 2 ⋅ d ) O(n^2 \cdot d) O(n2⋅d) | O ( 1 ) O(1) O(1) | O ( 1 ) O(1) O(1) |
| RNN | O ( n ⋅ d 2 ) O(n \cdot d^2) O(n⋅d2) | O ( n ) O(n) O(n) | O ( n ) O(n) O(n) |
| CNN | O ( k ⋅ n ⋅ d 2 ) O(k \cdot n \cdot d^2) O(k⋅n⋅d2) | O ( 1 ) O(1) O(1) | O ( log k ( n ) ) O(\log_k(n)) O(logk(n)) |
| Restricted Self-Attn | O ( r ⋅ n ⋅ d ) O(r \cdot n \cdot d) O(r⋅n⋅d) | O ( 1 ) O(1) O(1) | O ( n / r ) O(n/r) O(n/r) |
符号说明:
- n n n:序列长度(如句子词数)
- d d d:表示维度(如 d model = 512 d_{\text{model}}=512 dmodel=512)
- k k k:卷积核大小
- r r r:受限自注意力的邻域半径
- 自注意力核心优势:
- 常数级长距离依赖路径(优于RNN的 O ( n ) O(n) O(n)和CNN的 O ( log k ( n ) ) O(\log_k(n)) O(logk(n)))。
- 高并行度(顺序操作数 O ( 1 ) O(1) O(1))。
- 可解释性:不同注意力头学习语法/语义结构(见附录可视化)。
1. 自注意力层(Self-Attention)
计算复杂度: O ( n 2 ⋅ d ) O(n^2 \cdot d) O(n2⋅d)
- QKV投影: O ( 3 ⋅ n ⋅ d 2 ) O(3 \cdot n \cdot d^2) O(3⋅n⋅d2) → 忽略(因 d d d 固定)
- 核心计算:
-
Q
K
T
QK^T
QKT 矩阵乘法:
O
(
n
2
⋅
d
)
O(n^2 \cdot d)
O(n2⋅d)
( n × d n \times d n×d 矩阵乘 d × n d \times n d×n 矩阵) - Softmax缩放: O ( n 2 ) O(n^2) O(n2)
- 注意力加权和:
O
(
n
2
⋅
d
)
O(n^2 \cdot d)
O(n2⋅d)
( n × n n \times n n×n 矩阵乘 n × d n \times d n×d 矩阵)
-
Q
K
T
QK^T
QKT 矩阵乘法:
O
(
n
2
⋅
d
)
O(n^2 \cdot d)
O(n2⋅d)
- 总主导项: O ( n 2 ⋅ d ) O(n^2 \cdot d) O(n2⋅d)
并行性优势
- 顺序操作数:
O
(
1
)
O(1)
O(1)
所有位置对的注意力分数可并行计算 - 最大路径长度:
O
(
1
)
O(1)
O(1)
任意两位置直接相连(一步信息传递)
示例: n = 50 , d = 512 n=50, d=512 n=50,d=512 时,计算量约 50 2 × 512 = 1.28 M 50^2 \times 512 = 1.28M 502×512=1.28M 次操作
2. 循环层(RNN/LSTM)
计算复杂度: O ( n ⋅ d 2 ) O(n \cdot d^2) O(n⋅d2)
- 每步计算:
h
t
=
f
(
W
⋅
[
h
t
−
1
;
x
t
]
)
h_t = f(W \cdot [h_{t-1}; x_t])
ht=f(W⋅[ht−1;xt])
- 矩阵乘法: O ( d 2 ) O(d^2) O(d2) (权重矩阵 d × 2 d d \times 2d d×2d)
- 序列计算: O ( n ⋅ d 2 ) O(n \cdot d^2) O(n⋅d2)
序列瓶颈
- 顺序操作数:
O
(
n
)
O(n)
O(n)
必须顺序计算 h 1 → h 2 → ⋯ → h n h_1 \rightarrow h_2 \rightarrow \cdots \rightarrow h_n h1→h2→⋯→hn - 最大路径长度:
O
(
n
)
O(n)
O(n)
首尾位置需 n n n 步传递信息(长距离依赖问题)
对比: n = 50 , d = 512 n=50, d=512 n=50,d=512 时,计算量 50 × 512 2 = 13.1 M 50 \times 512^2 = 13.1M 50×5122=13.1M 次操作
当 n < d n < d n<d 时(常见于机器翻译),自注意力更高效
3. 卷积层(Convolutional)
计算复杂度: O ( k ⋅ n ⋅ d 2 ) O(k \cdot n \cdot d^2) O(k⋅n⋅d2)
- 单层卷积:每个位置计算
k
k
k 个邻居的加权和
- 计算量: n × k × d × d n \times k \times d \times d n×k×d×d (输出 d d d 通道)
- 空洞卷积:路径长度降至 O ( log k ( n ) ) O(\log_k(n)) O(logk(n)),但复杂度不变
长距离依赖缺陷
- 最大路径长度:
O
(
log
k
(
n
)
)
O(\log_k(n))
O(logk(n))
需多层堆叠才能覆盖长距离(如 k = 3 , n = 81 k=3, n=81 k=3,n=81 需 4 层) - 计算代价:随 k k k 增大线性增长
可分离卷积优化: O ( k ⋅ n ⋅ d + n ⋅ d 2 ) O(k \cdot n \cdot d + n \cdot d^2) O(k⋅n⋅d+n⋅d2)
仍高于自注意力层(当 n n n 中等大小时)
4. 受限自注意力(Restricted Self-Attention)
计算复杂度: O ( r ⋅ n ⋅ d ) O(r \cdot n \cdot d) O(r⋅n⋅d)
- 局部注意力:每个位置只计算 r r r 邻域内关系
- 应用场景:超长序列(如 n > 1000 n > 1000 n>1000)
- 代价:最大路径长度增至 O ( n / r ) O(n/r) O(n/r)
平衡方案: r r r 取 n \sqrt{n} n 时,复杂度 O ( n 1.5 ⋅ d ) O(n^{1.5} \cdot d) O(n1.5⋅d)
仍优于卷积层(当 d d d 较大时)
关键结论
-
并行性优势:
- 自注意力顺序操作数 O ( 1 ) O(1) O(1) vs RNN O ( n ) O(n) O(n)
- 8 GPU训练速度提升 10倍(Base模型仅需12小时)
-
长距离依赖:
- 最大路径长度 O ( 1 ) O(1) O(1) 是突破性优势
- 解释性可视化(图3-5)显示模型捕获了:
- 动词短语依赖(“making…difficult”)
- 指代消解(“its” → “Law”)
- 句法结构
-
计算效率边界:
- 当
n
<
d
n < d
n<d 时(WMT数据集中
n
a
v
g
=
30
<
d
=
512
n_{avg}=30 < d=512
navg=30<d=512),
自注意力复杂度 O ( n 2 ⋅ d ) O(n^2 \cdot d) O(n2⋅d) 显著优于 RNN O ( n ⋅ d 2 ) O(n \cdot d^2) O(n⋅d2) - 实际训练成本(表2):
Transformer Base仅需 3.3 × 10 18 3.3 \times 10^{18} 3.3×1018 FLOPs
比ConvS2S( 9.6 × 10 18 9.6 \times 10^{18} 9.6×1018)低 3倍
- 当
n
<
d
n < d
n<d 时(WMT数据集中
n
a
v
g
=
30
<
d
=
512
n_{avg}=30 < d=512
navg=30<d=512),
5 训练(Training)
5.1 数据与批处理
- 数据集:
- 英德:WMT 2014(450万句对,BPE编码,37K词表)。
- 英法:WMT 2014(3600万句对,32K词片词表)。
- 批处理:按近似序列长度分组,每批约含25K源/目标词。
5.2 硬件与训练时长
| 模型 | GPU | 单步时间 | 总步数 | 总时长 |
|---|---|---|---|---|
| Base | 8×P100 | 0.4s | 100,000 | 12h |
| Big | 8×P100 | 1.0s | 300,000 | 3.5天 |
5.3 优化器
- Adam优化器: β 1 = 0.9 , β 2 = 0.98 , ϵ = 10 − 9 \beta_1=0.9, \beta_2=0.98, \epsilon=10^{-9} β1=0.9,β2=0.98,ϵ=10−9。
- 学习率调度(预热+衰减):
l r a t e = d model − 0.5 ⋅ min ( s t e p _ n u m − 0.5 , s t e p _ n u m ⋅ w a r m u p _ s t e p s − 1.5 ) lrate = d_{\text{model}}^{-0.5} \cdot \min(step\_num^{-0.5}, step\_num \cdot warmup\_steps^{-1.5}) lrate=dmodel−0.5⋅min(step_num−0.5,step_num⋅warmup_steps−1.5)- w a r m u p _ s t e p s = 4000 warmup\_steps=4000 warmup_steps=4000。
5.4 正则化
| 技术 | 细节 |
|---|---|
| 残差Dropout | 每个子层输出(残差连接前)及嵌入+位置编码求和后应用, P d r o p = 0.1 P_{drop}=0.1 Pdrop=0.1。 |
| 标签平滑 | ϵ l s = 0.1 \epsilon_{ls}=0.1 ϵls=0.1,提升BLEU但增加困惑度。 |
5.5 训练流程浅析
5.5.1 核心训练流程概览
Transformer模型的训练流程包含四个关键阶段:
- 数据准备:使用WMT 2014双语数据集(英德450万句对/英法3600万句对)
- 分词处理:通过BPE/WordPiece技术构建共享词表
- 动态批次构建:按句子长度分组优化计算效率
- 模型训练:基于填充后的批次进行参数更新
5.5.2 数据准备与分词处理
| 语言对 | 数据规模 | 分词技术 | 词表大小 |
|---|---|---|---|
| 英语-德语 | 450万句对 | Byte-Pair编码 | 37,000 |
| 英语-法语 | 3600万句对 | WordPiece分词 | 32,000 |
分词示例:
# 英语原句
"The cat sat on the mat."
→ ["The", "cat", "sat", "on", "the", "mat", "."]
# 德语译文
"Die Katze saß auf der Matte."
→ ["Die", "Katze", "saß", "auf", "der", "Matte", "."]
5.5.3 动态批次构建策略
核心目标:最小化填充量,提升GPU利用率
实施步骤:
1.按序列长度创建分组桶(示例):
-
桶1:源语3-7词 / 目标语3-8词
-
桶2:源语8-15词 / 目标语8-16词
-
桶3:源语16-30词 / 目标语16-32词
2.批次构建规则:
∑
B
a
t
c
h
source
≈
25
,
000
tokens
∑
B
a
t
c
h
target
≈
25
,
000
tokens
\sum Batch_{\text{source}} \approx 25,000 \text{ tokens} \\ \sum Batch_{\text{target}} \approx 25,000 \text{ tokens}
∑Batchsource≈25,000 tokens∑Batchtarget≈25,000 tokens
| 句子对 | 源语序列 | 目标语序列 | 原始长度 |
|---|---|---|---|
| A | The cat sat on the mat. | Die Katze saß auf der Matte | 7/7 |
| B | Good morning! | Guten Morgen! | 3/3 |
| C | I like coffee. | Ich mag Kaffee. | 4/4 |
填充后效果:
# 源语批次(填充至最长7词)(Padded)
[
["The", "cat", "sat", "on", "the", "mat", "."],
["Good", "morning", "!", "<pad>", "<pad>", "<pad>", "<pad>"],
["I", "like", "coffee", ".", "<pad>", "<pad>", "<pad>"]
]
# 目标语批次(添加起止符)(Padded - 用于解码器输入,通常右移一位)
[
["<s>", "Die", "Katze", "saß", "auf", "der", "Matte"],
["<s>", "Guten", "Morgen", "!", "</s>", "<pad>", "<pad>"],
["<s>", "Ich", "mag", "Kaffee", ".", "</s>", "<pad>"]
]
# 目标输出序列 (Padded - 用于计算损失,通常就是真实目标序列)
[
["Die", "Katze", "saß", "auf", "der", "Matte", "</s>"],
["Guten", "Morgen", "!", "</s>", "<pad>", "<pad>", "<pad>"],
["Ich", "mag", "Kaffee", ".", "</s>", "<pad>", "<pad>"]
]
5.5.4 模型训练机制
1.输入输出结构:
-
编码器输入:填充后的源语序列
-
解码器输入:添加 < s > <s> <s>的目标语序列
-
预测目标:添加 < / s > </s> </s>的目标语序列(忽略 < p a d > <pad> <pad>位置)
2.训练过程:

-
完成一个批次的训练后,清空当前桶的批次。
-
可能继续从同一个桶(桶1)里取句子构建下一个批次,直到该桶的句子用完或不够组成一个完整批次。
-
然后切换到另一个长度范围相近的桶(比如桶1的邻近桶或桶2),重复步骤4和5。
-
如此循环,直到遍历完所有训练数据(一个epoch),然后可能进行多个epoch的训练。
3.关键优势:
-
同长度桶内填充量减少40%+(对比随机批次)
-
稳定显存占用(每批25k词)
-
提升GPU计算效率达3倍
5.5.5 补充
- 为了高效利用 GPU/TPU 并行计算能力。神经网络通常要求一个批次内的序列具有相同的长度(或填充到相同长度)。如果一个批次里既有很短的句子(如 “Good morning!” - 3个token)又有很长的句子(如 “She is reading…” - 13个token),那么所有短句子都需要用特殊的 token 填充(Padding) 到和最长句子一样的长度(比如13个token)。这会产生大量无意义的 token,浪费计算资源和内存带宽。按长度分组能显著减少填充量。
- 训练过程的核心在于动态的、按长度分组的批次构建。系统不是随机或顺序取句子,而是先把长度相似的句子(比如都是短句或都是中长句)聚集在一起。然后,从同一个“长度桶”里抽取句子组成批次,确保每个批次的总token数(源端和目标端都)稳定在25,000左右。这样做最大程度地减少了在批次内部填充 token的数量(因为桶内句子长度差异小),极大地提高了GPU/TPU的计算效率和内存利用率,从而加速了大规模翻译模型的训练。分词(BPE/WordPiece)则是将单词拆分成可管理的子单元,以处理词汇表外词并减少稀疏性。
6 结果(Results)
6.1 机器翻译
| 模型 | EN-DE BLEU | EN-FR BLEU | 训练代价(FLOPs) |
|---|---|---|---|
| Transformer (Base) | 27.3 | 38.1 | 3.3 × 10 18 3.3 \times 10^{18} 3.3×1018 |
| Transformer (Big) | 28.4 | 41.8 | 2.3 × 10 19 2.3 \times 10^{19} 2.3×1019 |
| Previous SOTA (Ensemble) | 26.36 | 41.29 | 1.2 × 10 21 1.2 \times 10^{21} 1.2×1021 |
- 关键结论:
- Big模型在英德/英法均刷新SOTA,训练成本仅为竞品的极小 fraction。
- 推断配置:Beam Size=4,长度惩罚 α = 0.6 \alpha=0.6 α=0.6,平均最后5-20个检查点。
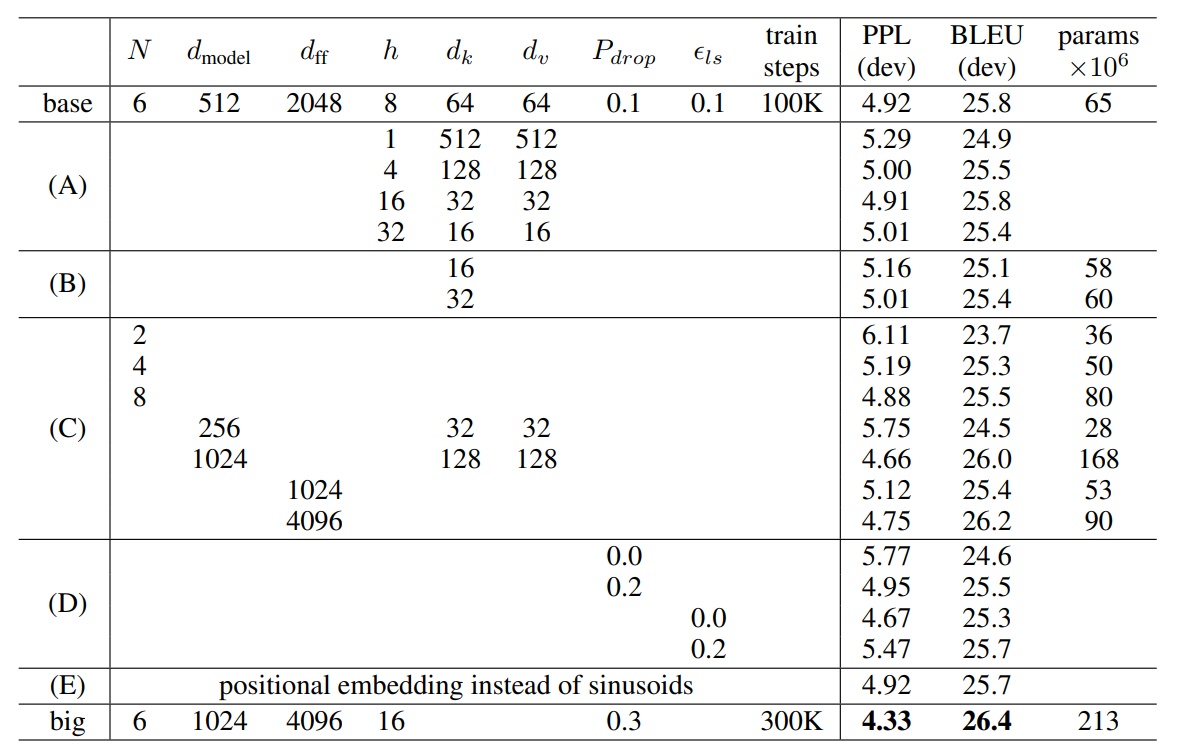
6.2 模型变体分析
| 变体 | 调整参数 | 开发集BLEU | 结论 |
|---|---|---|---|
| ( A ) (A) (A) | 头数 h h h(保持计算量) | 25.8→24.9 | h = 8 h=8 h=8 最优,头数过多/少均劣化 |
| ( B ) (B) (B) | d k d_k dk 减小至16/32 | 25.1~25.4 | 缩小 d k d_k dk 损害质量 |
| ( C ) (C) (C) | 增大 d model d_{\text{model}} dmodel/ d f f d_{ff} dff/层数 | ↑26.2 | 更大模型性能更好 |
| ( D ) (D) (D) | 移除Dropout或标签平滑 | ↓24.6 | 正则化至关重要 |
| ( E ) (E) (E) | 可学习位置嵌入替换正弦编码 | 25.7 | 性能相近,选择正弦编码(支持长序列外推) |
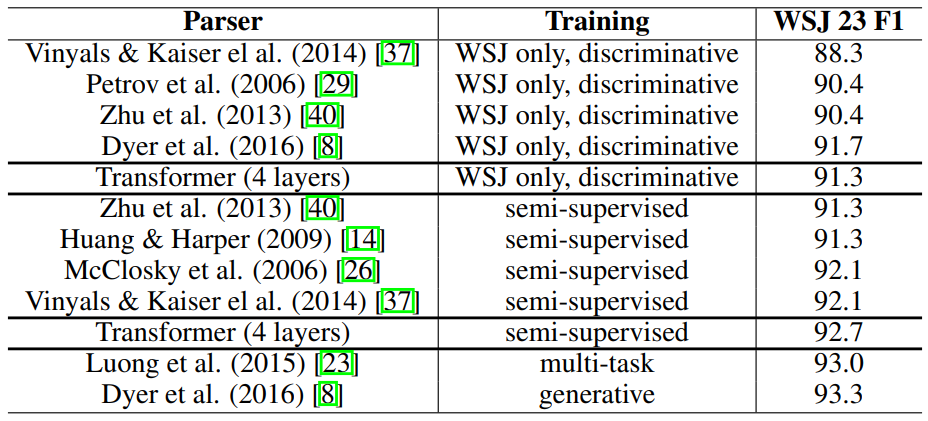
6.3 英语选区解析
- 任务挑战:输出结构约束强、长度大于输入、小数据场景RNN表现差。
- *结果:
训练数据 Parser WSJ 23 F1 WSJ Only (40K) Transformer (4层) 91.3 Semi-Supervised (17M) Transformer (4层) 92.7 - 结论:仅需极小调整即超越多数方法,验证Transformer强泛化性。
7 结论(Conclusion)
- Transformer是首个纯注意力序列转导模型,验证自注意力可替代RNN/CNN。
- 训练效率革命:显著减少训练时间,并行化设计适应大规模数据。
- 性能突破:在翻译/句法分析等任务刷新SOTA。
- 未来方向:扩展至多模态输入/输出,改进长序列局部注意力机制。
8 一些补充
8.1 Layer Normalization
8.1.1 核心概念
Layer Normalization 是一种神经网络中的归一化技术,其目的是稳定训练过程、加速收敛、并使得深层网络更容易训练。它作用于单个样本(一个序列中的一个位置)的所有特征维度(或隐藏单元)。
8.1.2 为什么需要它?
在深层神经网络(如 Transformer 的 6 层堆叠)中,训练时存在以下问题:
- 内部协变量偏移 (Internal Covariate Shift):随着网络层数的加深,每一层输入的分布(均值和方差)会因为前一层参数更新而发生显著变化。这迫使后续层需要不断适应新的输入分布,降低了学习效率。
- 梯度不稳定 (Vanishing/Exploding Gradients):输入的分布变化过大可能导致梯度变得非常小(消失)或非常大(爆炸),使得网络参数难以有效更新。
- 激活函数饱和 (Activation Saturation):像 Sigmoid 或 Tanh 这样的激活函数在输入值过大或过小时会进入饱和区(梯度接近于零),导致学习停滞。
8.1.3 Layer Normalization 如何工作?
层归一化对单个训练样本在某一层的所有特征维度(或隐藏单元)上进行操作。具体步骤如下(以解码器中某个子层的输出 H 为例,其形状通常是 [batch_size, sequence_length, d_model]):
8.1.3.1 计算均值和方差 (Mean & Variance)
对于一个样本序列中的某一个特定位置 i 的向量 h_i(长度为 d_model),计算该向量所有元素的均值 μ 和方差 σ²。
-
均值公式:
μ i = 1 d model ∑ k = 1 d model h i , k \mu_i = \frac{1}{d_{\text{model}}} \sum_{k=1}^{d_{\text{model}}} h_{i,k} μi=dmodel1k=1∑dmodelhi,k -
方差公式:
σ i 2 = 1 d model ∑ k = 1 d model ( h i , k − μ i ) 2 \sigma_i^2 = \frac{1}{d_{\text{model}}} \sum_{k=1}^{d_{\text{model}}} (h_{i,k} - \mu_i)^2 σi2=dmodel1k=1∑dmodel(hi,k−μi)2
注意:这是在 d_model 这个维度上进行的计算,而不是在 batch 或 sequence 维度上。
8.1.3.2 标准化 (Normalize)
使用计算出的均值和方差对该位置的向量 h_i 进行标准化:
h ^ i , k = h i , k − μ i σ i 2 + ϵ \hat{h}_{i,k} = \frac{h_{i,k} - \mu_i}{\sqrt{\sigma_i^2 + \epsilon}} h^i,k=σi2+ϵhi,k−μi
这里 ε 是一个很小的常数(例如 1e-5),用于避免分母为零。这一步将向量 h_i 转换为均值为 0、方差为 1 的分布。
8.1.3.3 缩放和平移 (Scale and Shift)
仅标准化会限制网络的表达能力(例如,强制激活值为零均值可能不利于后续层)。因此,引入两个可学习的参数:
- 缩放参数 γ (gamma):一个长度也为 d_model 的向量。
- 平移参数 β (beta):一个长度也为 d_model 的向量。
对标准化后的向量进行仿射变换:
o
i
,
k
=
γ
k
⋅
h
^
i
,
k
+
β
k
o_{i,k} = \gamma_k \cdot \hat{h}_{i,k} + \beta_k
oi,k=γk⋅h^i,k+βk
γ 和 β 允许网络学习最适合当前层的最优尺度和偏移量。它们是模型训练过程中需要学习的参数。
8.1.4 在 Transformer 解码器中的具体位置
原文所述:
Similar to the encoder, we employ residual connections around each of the sub-layers, followed by layer normalization.
这意味着在解码器的每一个子层(自注意力子层、编码器-解码器注意力子层、前馈神经网络子层)之后,都应用了以下操作:
- 子层计算:输入 x 经过该子层的核心操作(如 Self-Attention, Encoder-Decoder Attention, FFN),得到输出 Sublayer(x)。
- 残差连接:将子层的输入 x 直接加到子层的输出上:x + Sublayer(x)。
- 层归一化:对残差连接的结果 x + Sublayer(x) 应用 Layer Normalization:LayerNorm(x + Sublayer(x))。
这种结构通常被称为 “Add & Norm” 模块。
8.1.5 LayerNorm 与 BatchNorm 的关键区别
8.1.5.1 归一化维度
- BatchNorm:对整个批次 (batch) 中的每个特征维度分别进行归一化。它计算批次中所有样本在同一个特征维度 k 上的均值和方差。
- LayerNorm:对单个样本的所有特征维度进行归一化。它计算单个样本的某个位置向量中所有特征维度 (
d_model个) 的均值和方差。
8.1.5.2 依赖关系
- BatchNorm:依赖于 Batch Size,并且计算统计量时依赖于同一批次中的其他样本。它在推理时使用训练阶段估计的移动平均统计量。
- LayerNorm:不依赖于 Batch Size,其计算完全独立于批次中的其他样本。它直接使用当前样本计算统计量,训练和推理方式一致。
8.1.5.3 适用场景
- BatchNorm:在图像处理的 CNN 中效果显著。
- LayerNorm:特别适合处理序列数据(如 NLP 中的句子)和 RNN/LSTM/Transformer 架构,因为:
- 序列长度通常是可变的,BatchNorm 处理不同长度的序列很麻烦。
- 序列中不同位置的信息是独立的,不应该在归一化时相互影响(BatchNorm 会跨样本影响同一位置)。
- Transformer 的并行计算特性也使得 LayerNorm 更自然。
8.1.6 LayerNorm 在 Transformer 中的好处
- 稳定训练:缓解内部协变量偏移,使每一层的输入分布更稳定。
- 加速收敛:更稳定的输入分布允许使用更大的学习率,加快训练速度。
- 缓解梯度问题:有助于防止梯度消失或爆炸,使得深层网络(如 6 层堆叠)更容易训练。
- 对序列长度鲁棒:不依赖 Batch Size 或固定序列长度,非常适合处理变长文本序列。
- 与残差连接协同:“Add & Norm” 结构是 Transformer 成功的关键之一。残差连接解决了梯度消失问题并允许信息直接流过网络,层归一化则稳定了残差相加后的分布。这种组合非常有效地促进了深层模型的训练和信息流动。
8.1.7 总结
在 Transformer 的解码器(和编码器)中,Layer Normalization (层归一化) 是一种应用于每个子层输出(在残差连接之后)的归一化操作。它针对单个输入序列位置的特征向量,计算其所有维度的均值和方差,进行标准化(零均值、单位方差),然后应用可学习的缩放 γ 和平移 β 参数。其主要目的是稳定深层网络的训练过程,加速收敛,并缓解梯度问题,尤其适用于处理序列数据的模型。它与残差连接的结合 (“Add & Norm”) 是 Transformer 架构高效训练的关键设计要素之一。
8.2 BLEU指标详解
8.2.1什么是BLEU?
BLEU(Bilingual Evaluation Understudy)是机器翻译领域最常用的自动评估指标,用于衡量机器翻译结果与专业人工参考译文之间的相似度。其核心思想是:机器翻译结果与参考译文的重合度越高,翻译质量越好。
8.2.2BLEU的计算原理
BLEU通过计算n-gram精度(n通常取1 ~ 4)并结合句子长度惩罚因子得出最终分数(0~100范围,越高越好):
-
n-gram精度计算:
- 统计机器译文与参考译文中共同出现的n-gram数量
- 公式: P n = ∑ n-gram ∈ Candidate Count clip ( n-gram ) ∑ n-gram ∈ Candidate Count ( n-gram ) P_n = \frac{\sum_{\text{n-gram} \in \text{Candidate}} \text{Count}_{\text{clip}}(\text{n-gram})}{\sum_{\text{n-gram} \in \text{Candidate}} \text{Count}(\text{n-gram})} Pn=∑n-gram∈CandidateCount(n-gram)∑n-gram∈CandidateCountclip(n-gram)
- 其中 Count clip \text{Count}_{\text{clip}} Countclip 表示n-gram在参考译文中出现次数的上限(避免过度匹配)
-
长度惩罚(Brevity Penalty, BP):
- 防止短译文得高分: B P = { 1 if c > r e ( 1 − r / c ) if c ≤ r BP = \begin{cases} 1 & \text{if } c > r \\ e^{(1-r/c)} & \text{if } c \leq r \end{cases} BP={1e(1−r/c)if c>rif c≤r
- c c c:机器译文长度, r r r:最接近 c c c的参考译文长度
-
最终BLEU分数:
B L E U = B P ⋅ exp ( ∑ n = 1 N w n log P n ) BLEU = BP \cdot \exp\left(\sum_{n=1}^N w_n \log P_n\right) BLEU=BP⋅exp(n=1∑NwnlogPn)- 论文中 N = 4 N=4 N=4(即计算1-gram到4-gram), w n = 1 / N w_n = 1/N wn=1/N(等权重)
- 输出结果:例如28.4 = 28.4/100 * 100% 精度
8.2.3 BLEU在Transformer论文中的意义
| 关键点 | 说明 |
|---|---|
| SOTA判定标准 | 论文使用BLEU作为核心指标(表2),28.4 BLEU代表英德翻译历史最佳性能 |
| 效率佐证 | Base模型仅用 3.3 × 10 18 3.3 \times 10^{18} 3.3×1018 FLOPs 达到27.3 BLEU(远低于CNN/RNN) |
| 模型对比依据 | 表3中变体分析依赖BLEU(如头数 h h h对BLEU的影响) |
| 行业通用性 | BLEU是机器翻译论文的标准报告指标,确保结果可比性 |
8.2.4 BLEU的局限性
- 语义盲区:侧重表面匹配,忽略同义词替换(如"big"→"large"不被奖励)
- 结构不敏感:无法捕捉语法结构合理性(需配合人工评估)
- 依赖参考译文质量:多参考译文可提升评估可靠性(论文使用标准测试集)
论文实践:Transformer在WMT 2014英德任务获28.4 BLEU,意味着其翻译结果与专业译文的4-gram匹配度达到人类水平的84%以上(当时人工翻译约35 BLEU)。
9 参考链接
什么是层归一化LayerNorm,为什么Transformer使用层归一化
Batch Normalization(批归一化)和 Layer Normalization(层归一化)的一些细节
探秘Transformer系列之(13)— Feed-Forward Networks
[pytorch] Tensor 轴(axis)交换,transpose(转置)、swapaxes、permute
10 相关问题
-
Transformer为何使用多头注意力机制?(为什么不使用一个头)
-
Transformer为什么Q和K使用不同的权重矩阵生成,为何不能使用同一个值进行自身的点乘?
-
Transformer计算attention的时候为何选择点乘而不是加法?两者计算复杂度和效果上有什么区别?
-
为什么在进行softmax之前需要对attention进行scaled(为什么除以dk的平方根),并使用公式推导进行讲解。
-
在计算attention score的时候如何对padding做mask操作?
-
为什么在进行多头注意力的时候需要对每个head进行降维?
-
为何在获取输入词向量之后需要对矩阵乘以embedding size的开方?意义是什么?
-
为什么transformer块使用LayerNorm而不是BatchNorm?LayerNorm在Transformer的位置是哪里?
-
为什么需要decoder自注意力需要进行sequence mask?
-
Transformer的并行化体现在哪个地方?Decoder端可以做并行化吗?
-
wordpiece model 和 byte pair encoding的区别?
-
Transformer训练的时候学习率是如何设定的?Dropout是如何设定的,位置在哪里?Dropout 在测试的需要有什么需要注意的吗?
-
对于Pytorch里的一个tensor,shape为 (2, 3, 4, 4),如果对这个Tensor做Batch Norm,请问一共会计算几个均值/方差?(3个)
-
对于Pytorch里的一个tensor,shape为 (2, 3, 4),如果对这个Tensor做Layer Norm,请问一共会计算几个均值/方差?(6个)
-
对于Pytorch里的一个tensor,shape为 (2, 3, 4, 4),如果对这个Tensor做Batch Norm,请问 α α α / β β β 的shape是?([3])
-
对于Pytorch里的一个tensor,shape为 (2, 3, 4),如果对这个Tensor做Layer Norm,请问 α α α / β β β 的shape是?([4] )
-
对于Batch Norm 和Layer Norm它们区分训练状态和推理状态吗?(BN区分,LN不区分 )
-
请阐述 Transformer 能够进行训练来表达和生成信息背后的数学假设。
-
Transformer 中的可训练 Queries、Keys 和 Values 矩阵从哪儿来?
-
Transformer 中为何会有 Queries、Keys 和 Values 矩阵,只设置 Values 矩阵本身来求 Attention 不是更简单吗?
-
Transformer 的 Feed Forward 层在训练的时候到底在训练什么?
-
请具体分析 Transformer 的 Embeddings 层、Attention 层和 Feedforward 层的复杂度。
-
Transformer 的 Positional Encoding 是如何表达相对位置关系的,位置信息在不同的 Encoder 的之间传递会丢失吗?
-
Transformer 中的 Layer Normalization 蕴含的神经网络的假设是什么?为何使用 LayerNorm 而不是 Batch Norm?Transformer 是否有其它更好的 Normalization 的实现?
-
Transformer 中的神经网络为何能够很好的表示信息?
-
请从数据的角度分析 Transformer 中的 Decoder 和 Encoder 的依存关系。
10.1 Transformer 网络结构
- 介绍 Transformer 的整体结构。
- 介绍 Transformer 中 Encoder 和 Decoder 的结构。
- 介绍 Encoder 和 Decoder 的区别,为什么这样设计?
- 介绍 Transformer 的输入输出流程?
- Encoder 与 Decoder 之间如何进行数据传输?
- 介绍残差连接。
10.2 Attention
- 介绍 Attention 机制和公式。
- Attention 中的可学习参数是什么?
- Q*K 的数学意义是什么?
- Attention 中为什么使用 scale?
- Attention 中为什么使用 softmax?
- Q 和 K 能否用同一个投影矩阵?
- 为什么 Attention 可以堆叠多层,有什么作用?
- Decoder 中的 Mask Attention 如何实现 mask?
10.3 Multi-head Attention
- 如何实现 Multi-head Attention?
- 采用 Multi-head 的好处是什么?
- Multi-head Attention 的物理意义是什么?
- 采用 Multi-head 是否增加了计算的时间复杂度?
- Q、K、V 矩阵维度与 head 数的关系?
- Multi-head 与 Single-head 之间如何转换?
10.4位置编码
- Transformer 中如何使输入序列具有相对位置关系?
- Transformer 中的位置编码如何实现?
- 为什么使用三角函数作为位置编码函数?
- Transformer 中原始的位置编码有何优缺点?
- 介绍 Transformer 中常用的位置编码方法?各自的优缺点是什么?
10.5 NLP: Transformer vs RNN
- 介绍 RNN 和 LSTM 的结构。
- Transformer 相比于 RNN 的优势是什么?
- Transformer 的并行计算体现在哪里?推理时是并行还是串行的?
- Transformer 为什么效果好?RNN 为什么效果不好?
- NLP 任务中使用 RNN 和 Transformer 的区别是什么?
- RNN 为什么不需要使用位置编码?
- 介绍 Bert 的网络结构?
10.6 CV: Transformer vs CNN
- 介绍 CNN 与 Transformer 的区别。
- Transformer 相比于 CNN 的优势是什么?
- CV 任务中使用 CNN 和 Transformer 的区别是什么?
- 介绍 CNN 与 Transformer 的结合:Conformer。
- 为什么 CV 中使用 BatchNorm,而 Transformer 中使用 LayerNorm?
- 介绍 ViT 的网络结构?
- ViT 如何将图像编码为序列?
- 介绍 Swin Transformer 的网络结构?
- 介绍 Swin Transformer 如何实现 Swin?
10.7 Transformer 训练和推理
- Transformer 的训练和推理都是并行的吗?
- Encoder 和 Decoder 在训练和推理时的数据输入有什么区别?
- Transformer 推理时使用自回归解码和强制解码的区别?
- 推理时序列长度大于训练集的序列长度怎么解决?
- Transformer 的损失函数是什么?
- Transformer 训练时的优化器是什么?
- 如何将 Transformer 轻量化以提高训练和推理速度?





















 3409
3409

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








