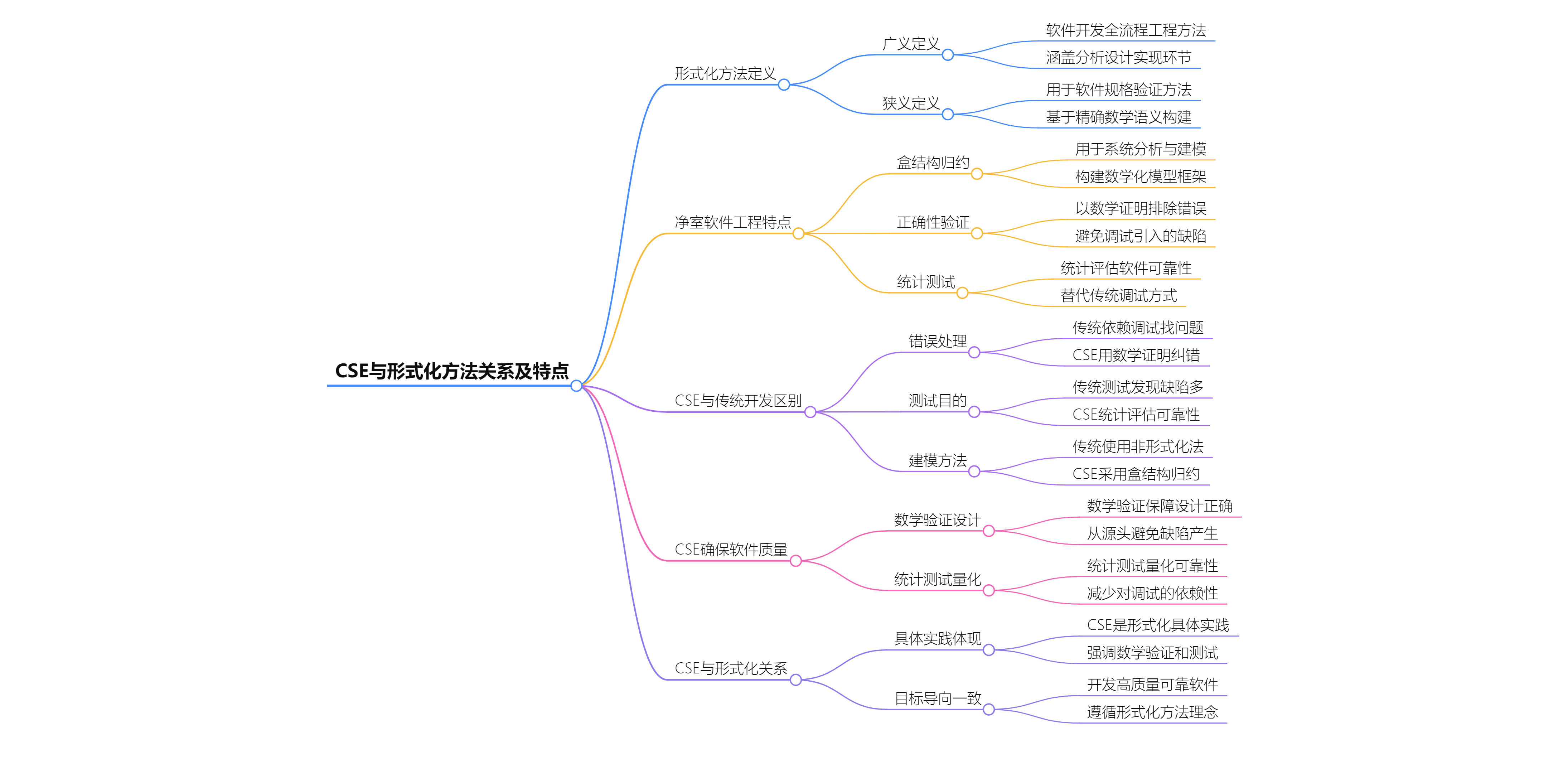
净室软件工程（CSE）是形式化方法在软件开发中的具体应用，它通过独特的机制和方法，与传统软件开发形成鲜明对比-优快云博客

本文链接：https://blog.youkuaiyun.com/blog_programb/article/details/149631459

在这里插入图片描述

净室软件工程（CSE）是形式化方法在软件开发中的具体应用，它通过独特的机制和方法，与传统软件开发形成鲜明对比，致力于保障软件质量。

形式化方法：为软件开发提供了基于严格数学的框架，从广义上涵盖了开发全过程的系统工程方法，狭义上则聚焦于软件规格说明和验证。
CSE的核心与优势：其核心的盒结构归约、正确性验证和统计测试，使其在错误处理上依靠数学证明而非调试，测试目的在于统计评估可靠性，建模方法也更为数学化，这些特点共同作用，通过数学验证避免缺陷引入，借助统计测试量化可靠性，从而确保软件质量。

这种将形式化方法具体化为可操作的工程实践的方式，让CSE在追求高质量、高可靠性软件的开发过程中具有独特价值。

净室软件工程（CSE）因强调通过数学验证确保设计正确性、以统计测试量化可靠性，且能最大限度减少缺陷引入，其应用场景主要集中在对软件可靠性、安全性和质量要求极高的领域。具体包括以下几类：

1. 安全关键系统

这类系统的故障可能导致人员伤亡、重大财产损失或环境灾难，对软件质量的容错率极低，CSE的严格验证机制能有效降低风险：

航空航天领域：如飞行器控制系统（自动驾驶、导航系统）、卫星姿态控制系统等。例如，航天器的飞控软件若出现错误，可能导致任务失败甚至航天器坠毁，CSE的正确性验证可提前排除设计缺陷。
医疗设备领域：如生命支持系统（呼吸机、心脏除颤器）、医疗影像诊断系统等。医疗设备软件的错误可能直接威胁患者生命，CSE通过数学证明确保核心功能的准确性。
核能与能源系统：如核电站监控系统、电力调度系统等。这类系统的软件故障可能引发能源泄漏、供电中断等严重事故，CSE的可靠性保障机制至关重要。

2. 高可靠性嵌入式系统

嵌入式系统通常运行在资源受限、环境复杂的场景中，且一旦部署后维护成本极高，需在开发阶段确保高可靠性：

工业控制领域：如智能制造中的生产线自动化控制软件、精密仪器控制系统（如半导体生产设备）。CSE的盒结构归约可清晰建模系统交互，避免逻辑漏洞。
汽车电子领域：尤其是自动驾驶的决策系统、刹车防抱死系统（ABS）等。汽车软件的可靠性直接关系到行车安全，CSE的统计测试能量化评估软件在极端场景下的表现。

3. 金融与关键业务系统

这类系统需保证数据准确性、交易完整性，且故障可能导致经济损失或信任危机：

金融交易系统：如高频交易算法、银行核心账务系统。CSE的正确性验证可确保交易逻辑无歧义，避免因计算错误导致的资金损失。
关键业务支撑系统：如大型企业的供应链管理核心模块、政府部门的政务数据处理系统。CSE通过严格的建模和验证，减少因软件缺陷导致的业务中断。

4. 军事与国防系统

军事软件的可靠性直接影响作战效能和国家安全，例如：

武器控制系统（导弹制导、无人机指挥系统）
加密通信系统（确保信息传输的安全性和完整性）

CSE通过数学化的设计和验证，能在复杂对抗环境中保证软件功能的稳定性。

总结

CSE的应用场景核心是**“零缺陷容忍”或“高可靠性需求”**，其通过形式化的建模、数学验证和统计测试，牺牲了部分开发效率以换取极高的软件质量，因此更适合对可靠性要求远高于开发成本和周期的领域。对于普通消费级软件（如手机APP、网页应用），因需求快速迭代且容错率较高，CSE的投入成本通常不符合性价比，应用较少。

你的总结已经非常清晰，下面我稍作补充和提炼，帮助更精准地理解CSE与形式化方法的关系：

如何理解CSE与形式化方法的关系？

形式化方法是“理论”，CSE是“实践”
形式化方法提供严格的数学工具和语义框架（如逻辑证明、形式化规约），而CSE是这些方法在软件开发中的系统化工程实践，将数学验证嵌入开发流程。
CSE是形式化方法的“子集与强化”
- 子集：CSE仅采用形式化方法中适合工程化的部分（如盒结构建模、正确性证明）。
- 强化：CSE通过统计测试补充了传统形式化方法对“实际运行可靠性”的验证缺口（数学证明无法覆盖所有运行时场景）。
共同目标：零缺陷的可靠性
形式化方法追求“数学正确性”，CSE进一步通过“不调试”原则（设计时即消除错误）和统计测试，将数学正确性转化为可量化的可靠性指标（如平均无故障时间）。

一句话总结

CSE是形式化方法在工业场景中的“务实化”——用数学证明确保设计无缺陷，用统计测试验证现实可靠性，两者互补实现“高可信软件”的开发。

净室软件工程（CSE）在软件开发中的具体应用步骤可归纳为以下五个阶段，每个阶段都融合了形式化方法与统计质量控制：

1. 需求分析（Requirements Analysis）

目标：精确定义用户需求，消除歧义。
方法：
- 与客户协作，将需求转化为数学化的规格说明（如基于函数的规约）。
- 使用盒结构规约：从黑盒（外部行为）→状态盒（状态机）→明盒（过程实现）逐步细化。

2. 形式化设计（Formal Design）

目标：通过数学模型确保设计的正确性。
方法：
- 基于函数的规范：用数学函数描述系统行为，避免自然语言的模糊性。
- 增量式设计：将系统分解为小的、可验证的增量模块，每个模块独立验证。

3. 正确性验证（Correctness Verification）

目标：在编码前通过数学证明消除缺陷（而非调试）。
方法：
- 对关键模块进行形式化证明（如使用逻辑推导验证算法是否符合规约）。
- 团队评审：开发人员通过同行审查和数学推演确认逻辑正确性。

4. 统计测试与认证（Statistical Testing & Certification）

目标：量化软件可靠性，而非发现缺陷。
方法：
- 使用模型（Usage Model）：基于用户实际操作场景生成测试用例。
- 统计抽样：通过有限测试用例推断系统整体可靠性（如计算平均无故障时间）。
- 软件认证：若统计结果达到预设标准（如99.9%可靠性），则通过认证。

5. 增量式开发与维护（Incremental Development & Maintenance）

目标：持续交付高质量增量，减少回归风险。
方法：
- 迭代开发：每个增量重复上述步骤（需求→设计→验证→测试）。
- 统计过程控制：监控每阶段的质量指标（如缺陷率），确保过程稳定性。

示例流程图

需求分析 → 形式化设计 → 正确性验证 → 统计测试 → 增量交付
   ↑           ↑           ↑           ↑           ↑
数学化规约 → 盒结构建模 → 数学证明 → 使用模型测试 → 持续迭代

关键差异总结

传统开发	CSE步骤
调试修复缺陷	数学证明预防缺陷
测试发现错误	统计测试量化可靠性
一次性交付	增量式验证与交付

通过以上步骤，CSE将形式化方法的严谨性与工程实践结合，适用于航天、金融等高可靠性场景。