2020秋PAT甲级满分代码（全网代码最简洁&思路最清晰之一）

最新推荐文章于 2023-05-24 22:36:25 发布

原创最新推荐文章于 2023-05-24 22:36:25 发布 · 2.5k 阅读

29 ·

CC 4.0 BY-SA版权

文章标签：

#pta

=====PTA===== 专栏收录该内容

6 篇文章

订阅专栏

本文详细介绍了三个算法问题的解决方案：根据熊猫体重公平分配奶量的最小总量计算，有限金钱购买连续土地的方案数，以及二叉树的左视图。涉及前缀和、尺取法和深度优先搜索等算法思想。

警告：代码虽然简洁（除了第四题），但是理解起来可能有些费力。

1 Panda and PP Milk (20分)

题意：n（n<=1e4）个熊猫排成一排等待喝奶，每个熊猫至少喝200ml奶。为了公平性，重的熊猫喝得奶要更多。每个熊猫只能看到与它相邻的两个熊猫喝了多少奶，相差大于100ml熊猫才能感到差别。给出n以及按顺序给出n个熊猫的重量，求需要奶的最少总量。可能坑点：用long long！

思路：类似前缀后缀的思想，正着遍历一遍记下从第一个熊猫开始，记下它左边的熊猫对他的影响；同理，再倒着遍历一遍记下从最后一个熊猫开始，记下它右边的熊猫对他的影响。这个影响是连续的，影响有3种情况（假设a[i]表示第i个熊猫的重量）：

1. if(a[i-1]<a[i]) pre[i]=pre[i-1]+1;

2. if(a[i-1]==a[i]) pre[i]=pre[i-1];

3. if(a[i-1]>a[i]) pre[i]=0;

最后，左右影响取一个最大值。

#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int N = 1e4+10;
ll n,a[N],pre[N],suf[N];
int main(){
	cin>>n;
	for(int i=1;i<=n;i++){
		cin>>a[i];
		if(i==1) continue;
		if(a[i]>a[i-1])
			pre[i]=pre[i-1]+1;
		else if(a[i]==a[i-1])
			pre[i]=pre[i-1];
		else
			pre[i]=0;	
	}			
	for(int i=n-1;i>=1;i--){
		if(a[i]>a[i+1])
			suf[i]=suf[i+1]+1;
		else if(a[i]==a[i+1])
			suf[i]=suf[i+1];
		else	
			suf[i]=0;
	}	
	ll ans=2LL*n;
	for(int i=1;i<=n;i++)
		ans+=1LL*max(pre[i],suf[i]);
	ans=ans*1LL*100;
	cout<<ans;
	return 0;
}

2 How Many Ways to Buy a Piece of Land (25分)

题意：n（n<=1e4）块地，总共有m（m<=1e9）块钱，只能买连续的地。给出每块地的价格，问总共有多少种买法。

思路1：尺取（没听过这个算法的建议看下面思路2）。我觉得我写的应该是标程，很明显的尺取题。只不过算方案数要记得去重。

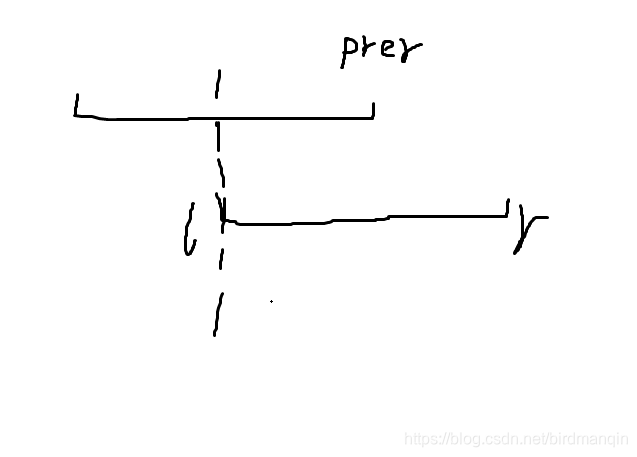
对于尺取的每个区间，方案数为（r-l+1）*（1+r-l+1）/2。但上图中，显然重复计算了[l,prer]这个区间，因此，要减去这个区间内的方案数。

#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int N = 1e4+10;
ll n,m,a[N];
int main(){
	cin>>n>>m;
	for(int i=1;i<=n;i++)
		cin>>a[i];
	ll l=1,r=1,sum=0,prer=0;
	ll ans=0;
	while(l<=n&&r<=n){
		while(r<=n&&sum+a[r]<=m)
			sum+=a[r++];
		//区间内至少有一个数 
		if(l<r){
			//这里的r其实是区间右边界+1，所以不用+1。 
			ans+=(r-l)*(r-l+1)/2LL;
			//是否有重复区间 
			if(prer>=l) ans-=(prer-l+1)*(prer-l+2LL)/2LL;
		}
		//记下右边界的值 
		prer=r-1;	
		sum-=a[l++];
	}
	cout<<ans;
	return 0;
}

思路2：直接枚举，及时break即可，没交过代码，只跑了样例，应该不会错。

#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int N = 1e4+10; 
ll n,m,sum,ans=0,a[N];
int main(void){
	cin>>n>>m;
	for(int i=1;i<=n;i++)
		cin>>a[i];
	for(int l=1;l<=n;l++){
		sum=0;
		for(int r=l;r<=n;r++){
			sum+=a[r];
			if(sum<=m) ans++;
			else break;
		}
	}
	cout<<ans;
	return 0;	
}

3 Left-View of Binary Tree (25分)

题意：给出含有n（n<=20）个节点的二叉树的中序以及前序遍历序列，输出该树的左视图。

思路：左视图其实就是每一层最左边的节点序列。实现就是柳婼大神思路，简单好用！

#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int N = 30;
int n,pre[N],in[N],ans[N],cnt=0;
void dfs(int prel,int prer,int inl,int inr,int dep){
	if(inl>inr) return ;
	int pos=inl;
	while(pos<=inr&&in[pos]!=pre[prel]) pos++;
	if(!ans[dep]){
		ans[dep]=pre[prel];
		cnt=max(cnt,dep);
	}
	dfs(prel+1,prel+pos-inl,inl,pos-1,dep+1);
	dfs(prel+pos-inl+1,prer,pos+1,inr,dep+1);	
}
int main(){
	cin>>n;
	for(int i=1;i<=n;i++)
		cin>>in[i];
	for(int i=1;i<=n;i++)
		cin>>pre[i];
	dfs(1,n,1,n,1);
	for(int i=1;i<=cnt;i++)
		printf("%d%c",ans[i],i==cnt?'\n':' ');
	return 0;
}

4 Professional Ability Test (30分)

题意：有点复杂，阅读理解题。n（n<=1000）个考试（节点），m个约束关系（有向边），每个约束由一个四元组表示（u,v,s,d）,代表只有考试u的得分不少于s时，才能考v，并且获得价值d块钱的代金券。给你一个考试序列。对于每个考试T，如果考试T是T的前置条件（即T在环中），那么认为这个考试序列是不一致的。

（1）如果一致，首先输出“Okay.”。然后如果对于序列中的每个考试T，如果这个考试没有前置考试（即入度为0），则输出“You may take test T directly.”；否者，输出通过这个考试的并且总分数S最少的路径（即从任意入度为0的点开始到它的最短路），如果不唯一，则输出总代金券（D）最多的路径。

（2）如果不一致，首先输出“Impossible.”。然后如果对于序列中的每个考试T，如果这个考试没有前置考试（即入度为0），则输出“You may take test T directly.”；否者，输出“Error.”。

思路1（比较暴力）：DFS判环，建反向图，对每个点跑Dijkstra最短路。

#include <bits/stdc++.h>
#define ll long long
#define pb push_back
using namespace std;
const int N = 1e3+10;
const int M = 1e6+10;
const int inf = 0x3f3f3f3f;
struct node{
	int to,sc,vou;
};
vector<int> g[N];
vector<node> rg[N];
int n,m,u,v,s,d,in[N],a[N],k;
int dis[N],vou[N],book[N],pre[N];
bool vis[N];
bool flag=0;
void dfs(int u,int x){
	if(flag) return ;
	for(int i=0;i<g[u].size();i++){
		if(g[u][i]==x){
			flag=1;
			return ;
		}
		if(book[g[u][i]]) continue;
		book[g[u][i]]=1;
		dfs(g[u][i],x);
		if(flag) return ;
	}
}
struct Node{
	int to,dis,vou;
	friend bool operator<(Node a,Node b){
		if(a.dis==b.dis)
			a.vou<b.vou;
		return a.dis>b.dis;
	}
};
void dijs(int st){
	for(int i=0;i<n;i++){
		dis[i]=inf;
		vou[i]=0;
		book[i]=0;
		pre[i]=-1;
	}
	priority_queue<Node> q;
	q.push(Node{st,0,0});
	dis[st]=0;
	while(!q.empty()){
		Node now = q.top();
		q.pop();
		int u = now.to;
		if(book[u]) continue;
		book[u]=1;
		for(int i=0;i<rg[u].size();i++){
			int v = rg[u][i].to;
			if(dis[v]>dis[u]+rg[u][i].sc){
				dis[v]=dis[u]+rg[u][i].sc;
				vou[v]=vou[u]+rg[u][i].vou;
				pre[v]=u;
				q.push(Node{v,dis[v],vou[v]});
			}else if(dis[v]==dis[u]+rg[u][i].sc){
				if(vou[v]<vou[u]+rg[u][i].vou){
					vou[v]=vou[u]+rg[u][i].vou;
					pre[v]=u;
					q.push(Node{v,dis[v],vou[v]});
				}
			}
		}	
	}
	int mind=inf,maxv=0,temp=0;
	for(int i=0;i<n;i++)
		if(vis[i]){
			if(mind>dis[i]){
				mind=dis[i];
				maxv=vou[i];
				temp=i;
			}else if(mind==dis[i]){
				if(maxv<vou[i]){
					maxv=vou[i];
					temp=i;
				}
			}
		}
	vector<int> ans;
	while(temp!=st){
		ans.pb(temp);
		temp=pre[temp];
	}
	ans.pb(st);
	int len = ans.size();
	for(int i=0;i<len;i++){
		printf("%d",ans[i]);
		if(i==len-1) printf("\n");
		else printf("->");
	}
	
}
int main(){
	cin>>n>>m;
	for(int i=1;i<=m;i++){
		cin>>u>>v>>s>>d;
		in[v]++;
		g[u].pb(v);
		rg[v].pb(node{u,s,d});
	}
	for(int i=0;i<n;i++)
		if(in[i]==0) vis[i]=1;
	cin>>k;
	bool no=0;
	for(int i=1;i<=k;i++){
		cin>>a[i];
		if(no) continue;
		flag=0;
		memset(book,0,sizeof book);
		dfs(a[i],a[i]);
		if(flag) no=1;
	}
	if(no){
		puts("Impossible.");	
		for(int i=1;i<=k;i++)
			if(vis[a[i]]) printf("You may take test %d directly.\n",a[i]);
			else puts("Error.");
	} 
	else{
		puts("Okay.");	
		for(int i=1;i<=k;i++){
			if(vis[a[i]]) printf("You may take test %d directly.\n",a[i]);
			else dijs(a[i]);
		}			
	} 	
	
	
	return 0;
}

思路2：首先声明，没有交过，只过了样例。还是dfs判环，加入一个超级源点N，指向所有入度为0的点，只跑一遍Dijkstra。

#include <bits/stdc++.h>
#define ll long long
#define pb push_back
using namespace std;
const int N = 1e3+10;
const int M = 1e6+10;
const int inf = 0x3f3f3f3f;
struct node{
	int to,sc,vou;
};
vector<node> g[N];
int n,m,u,v,s,d,in[N],a[N],k,source;
int dis[N],vou[N],book[N],pre[N];
bool vis[N];
bool flag=0;
void dfs(int u,int x){
	if(flag) return ;
	for(int i=0;i<g[u].size();i++){
		if(g[u][i].to==x){
			flag=1;
			return ;
		}
		if(book[g[u][i].to]) continue;
		book[g[u][i].to]=1;
		dfs(g[u][i].to,x);
		if(flag) return ;
	}
}
struct Node{
	int to,dis,vou;
	friend bool operator<(Node a,Node b){
		if(a.dis==b.dis)
			a.vou<b.vou;
		return a.dis>b.dis;
	}
};
void dijs(int st){
	for(int i=0;i<=n;i++){
		dis[i]=inf;
		vou[i]=0;
		book[i]=0;
		pre[i]=-1;
	}
	priority_queue<Node> q;
	q.push(Node{st,0,0});
	dis[st]=0;
	while(!q.empty()){
		Node now = q.top();
		q.pop();
		int u = now.to;
		if(book[u]) continue;
		book[u]=1;
		for(int i=0;i<g[u].size();i++){
			int v = g[u][i].to;
			if(dis[v]>dis[u]+g[u][i].sc){
				dis[v]=dis[u]+g[u][i].sc;
				vou[v]=vou[u]+g[u][i].vou;
				pre[v]=u;
				q.push(Node{v,dis[v],vou[v]});
			}else if(dis[v]==dis[u]+g[u][i].sc){
				if(vou[v]<vou[u]+g[u][i].vou){
					vou[v]=vou[u]+g[u][i].vou;
					pre[v]=u;
					q.push(Node{v,dis[v],vou[v]});
				}
			}
		}	
	}
}
int main(){
	cin>>n>>m;
	source=n;//超级源点为n 
	for(int i=1;i<=m;i++){
		cin>>u>>v>>s>>d;
		in[v]++;
		g[u].pb(node{v,s,d});
	}
	for(int i=0;i<n;i++)
		if(in[i]==0){
			vis[i]=1;
			g[source].pb(node{i,0,0});	
		} 
	cin>>k;
	bool no=0;
	for(int i=1;i<=k;i++){
		cin>>a[i];
		if(no) continue;
		flag=0;
		memset(book,0,sizeof book);
		dfs(a[i],a[i]);
		if(flag) no=1;
	}
	if(no){
		puts("Impossible.");	
		for(int i=1;i<=k;i++)
			if(vis[a[i]]) printf("You may take test %d directly.\n",a[i]);
			else puts("Error.");
	} 
	else{
		
		puts("Okay.");	
		dijs(source);
		for(int i=1;i<=k;i++){
			if(vis[a[i]]) printf("You may take test %d directly.\n",a[i]);
			else{
				vector<int> ans;
				int temp=a[i];
				while(temp!=source){
					ans.pb(temp);
					temp=pre[temp];
				}
				int len = ans.size();
				for(int i=len-1;i>=0;i--){
					printf("%d",ans[i]);
					if(i) printf("->");
					else printf("\n");
				}				
			}
		}			
	} 	
	return 0;
}