深度学习-相关学习笔记（持续更新）

自注意力机制（Self-Attention Mechanism）是深度学习中处理序列数据的一种方法，它允许模型在序列的不同位置之间建立直接的依赖关系，从而更好地捕捉序列数据中的时序特征。然而，在经典的Transformer模型中，自注意力机制的时间复杂度为O(L²)，其中L是序列的长度。当处理长序列时，这种全序列长度的计算方式会变得非常低效，因为它需要对序列中每对元素进行计算。

为了解决这个问题，ProbSparse自注意力机制被提出。其核心思想是使用一种概率方法来减少计算量，将全序列长度的时间复杂度降低到O(LlogL)。这种机制通过概率性的采样来选择重要的元素进行注意力计算，从而减少计算量，提高模型处理长序列数据的效率。

具体来说，ProbSparse自注意力机制在计算注意力分数时，不是对所有键（Key）进行遍历，而是根据一定的概率分布对键进行采样，然后计算查询（Query）与采样后的键之间的注意力分数。这样，模型可以只关注那些对当前查询最重要的键，从而显著降低计算复杂度。

点积注意力（Dot-Product Attention）

点积注意力（Dot-Product Attention），作为注意力机制的一种高效实现形式，因其计算效率高和表达能力强而被广泛应用于诸如Transformer架构等先进模型中。

#示例代码
import numpy as np
from scipy.special import softmax

def dot_product_attention(query, key, value):
    # 计算点积
    scores = np.dot(query, key.T).astype(np.float64)
    
    # 缩放分数
    d_k = key.shape[-1]
    scale = np.sqrt(d_k)
    scores /= scale.astype(np.float64)
    
    # 应用 softmax 函数
    attention_weights = softmax(scores, axis=-1)
    
    # 计算加权和
    output = np.dot(attention_weights, value)
    
    return output, attention_weights

# 示例数据
query = np.array([[1, 2], [3, 4]])
key = np.array([[2, 3], [4, 5]])
value = np.array([[5, 6], [7, 8]])

# 计算注意力
output, attention_weights = dot_product_attention(query, key, value)

print("输出：\n", output)
print("注意力权重：\n", attention_weights)

KL散度（ D(P||Q) ）

又称为相对熵或信息散度，是衡量两个概率分布之间差异的一种非对称性度量。

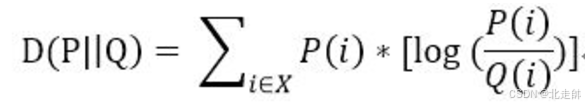
也可写作

代码和函数

.npy文件：

是NumPy（Numerical Python）库中用于保存数组数据的二进制文件格式。可用np.load()和np.save()函数来读写“.npy”文件

import numpy as np
 
# 创建一个NumPy数组
arr = np.array([1, 2, 3, 4, 5])
 
# 将数组保存为.npy文件
np.save('array.npy', arr)
 
# 加载.npy文件并将其转换回NumPy数组
loaded_arr = np.load('array.npy')
 
# 打印加载的数组
print(loaded_arr)

.npz文件

一种二进制文件格式，由 NumPy 库提供支持，用于存储多个数组对象。这种文件格式特别适用于需要高效存储和读取大量数值数据的场景，比如机器学习和科学计算领域。

.npz文件可以存储多个数组对象，每个数组都有一个名称。这使得在一个文件中存储多个相关数组变得非常方便。

.npz文件可以是压缩的（默认情况下是压缩的），这有助于减少文件大小，节省存储空间。压缩文件的扩展名通常是 .npz，未压缩的文件也可以使用 .npz 扩展名，但可以通过参数控制是否压缩。

import numpy as np

# 创建一些数组
array1 = np.array([1, 2, 3])
array2 = np.array([[4, 5], [6, 7]])

# 保存为 .npz 文件
np.savez('example.npz', array1=array1, array2=array2)

# 保存为压缩的 .npz 文件
np.savez_compressed('example_compressed.npz', array1=array1, array2=array2)

# 加载 .npz 文件
data = np.load('example.npz')

# 获取数据数组
X = data['array1']

# 查看数据形状
print("Data shape:", X.shape)
print("Data:", X)

.h5文件

教程：Using HDF5 with Python. Hierarchical Data Format (HDF) is a set… | by Jeril Kuriakose | Medium

# .h5文件的读取操作
store = pd.HDFStore('metr-la.h5')
'''查看store类型'''
print("store:",store)
df1 = store.df
print("df1:",df1)

.pkl文件

加载.pkl文件

import pickle

# 打开一个文件用于读取
with open('data.pkl', 'rb') as f:
    # 使用pickle.load()从文件中读取序列化的对象并还原为原来的Python对象
    loaded_data = pickle.load(f)

# 打印加载的数据
print(loaded_data)

在深度学习中，我们经常需要保存和加载训练好的模型。许多深度学习框架（如TensorFlow和PyTorch）都支持将模型保存为pkl格式文件或其他专用格式，以便后续使用。通过保存模型为pkl文件，我们可以方便地分享模型、在不同环境中部署模型，或者进行模型的版本控制。

import torch
import torch.nn as nn
import pickle

# 定义一个简单的神经网络模型
class SimpleModel(nn.Module):
    def __init__(self):
        super(SimpleModel, self).__init__()
        self.fc = nn.Linear(10, 1)

    def forward(self, x):
        return self.fc(x)

# 实例化模型并训练（此处省略训练过程）
model = SimpleModel()
# 假设model已经训练好...

# 保存模型参数到pkl文件
with open('model_params.pkl', 'wb') as f:
    pickle.dump(model.state_dict(), f)

# 从pkl文件中加载模型参数
with open('model_params.pkl', 'rb') as f:
    loaded_params = pickle.load(f)

# 实例化一个新模型并加载参数
new_model = SimpleModel()
new_model.load_state_dict(loaded_params)

在上面的代码中，我们定义了一个简单的神经网络模型，并将其参数保存为pkl文件。然后，我们从pkl文件中加载参数，并应用到一个新实例化的模型中。这样，我们就可以在不重新训练的情况下使用加载的模型参数进行预测或进一步的分析。

参考文章：

【Python】一文详细介绍 pkl格式文件_pkl文件-优快云博客

Informer：高效长序列时间序列预测模型（更新中）_informer时间序列预测-优快云博客

相对熵（KL散度）_ex～p(x) [ log p(s)-优快云博客