基于频域调制的低旁瓣随机雷达信号设计

基于频域调制法的低旁瓣随机雷达信号设计

1 引言

雷达正面临日益恶劣的电磁环境。敌方拥有多种技术手段来削弱雷达的有效性。使用确定性波形的传统雷达通常容易受到干扰、欺骗以及其他传感器对信号的干扰[1, 2]。由于其随机波形、低截获概率/低探测概率（LPI/LPD）特性以及良好的电子抗干扰（ECCM）能力，噪声雷达或随机信号雷达已被广泛应用于诸多领域，如合成孔径雷达/逆合成孔径雷达成像、地层穿透成像、监视等[2–6]。

然而，传统的噪声雷达/随机信号雷达容易被强回波信号致盲[7, 8]。为了缓解邻近目标的遮蔽效应，本文提出一种基于高斯形状功率谱密度（PSD）频谱整形的频域调制方法，用于设计具有低旁瓣的随机雷达信号。所设计的随机雷达信号的低旁瓣性能通过脉冲压缩的数值仿真进行了检验，并通过实测数据实验加以验证。此外，还研究了人体运动的极化微多普勒特性[9, 10]。

2 随机雷达信号设计

根据维纳‐辛钦定理，信号的自相关函数是其功率谱密度的逆傅里叶变换[7]。通过对设计的随机雷达信号的频谱进行高斯形状功率谱密度整形，可以实现低旁瓣性能，因为高斯函数的傅里叶变换仍是高斯函数[2,7]。同时，在频域中通过随机序列对设计的雷达信号的相位谱进行调制，以确保产生随机波形。

然后，设计的随机雷达信号的频谱可以表示为
$$ S(f) = G(f) \exp(j2\pi\psi(f)) $$ (1)

其中 $ G(f) $ 是设计的随机雷达信号的幅度谱，$ 2\pi\psi(f) $ 是设计的随机雷达信号的相位谱。随机雷达信号的功率谱密度为
$$ P_S(f) = |S(f)|^2 = |G(f) \exp(j2\pi\psi(f))|^2 = |G(f)|^2 $$ (2)

显然，基于(1)设计的随机雷达信号可以实现高斯功率谱密度。

假设 $ \psi_n \in [0, 1] $，$ 0 \leq n \leq N - 1 $ 是一个随机序列，则谱 $ S(f) $ 的离散形式可表示为
$$ S(n\Delta f) = G(n\Delta f) \exp(j2\pi\psi(n\Delta f)) $$ (3)

Then
$$ S(n) = G(n) \exp(j2\pi\psi(n)) $$ (4)

其中，$ N $ 是采样点数，$ B $ 是设计的随机雷达信号的带宽。$ \Delta f $ 是采样间隔，可表示为
$$ \Delta f = \frac{B}{N} $$ (5)

接下来，可以通过对随机雷达信号的频谱进行逆傅里叶变换，得到时域中的随机雷达信号
$$ s(n) = \text{IFFT}[S(n)] = \text{IFFT}[G(n) \exp(2\pi\psi(n))] $$ (6)

在(6)中，随机雷达信号是在奈奎斯特速率下设计的，所设计的随机雷达信号的带宽与采样频率相同。然而，在实际雷达系统中，采样频率通常是固定的，一般由数字设备（如任意波形发生器）决定。在大多数情况下，我们希望生成具有灵活带宽的雷达信号，而不是受限于固定采样频率的信号。在此情况下，我们可以通过在频域进行零填充，将设计的随机雷达信号上采样至雷达系统的采样频率，如图1所示。

显然，上采样的随机雷达信号仍然具有高斯功率谱密度，能够保证其低旁瓣性能。通过使用该方法，我们可以在雷达系统采样频率固定的情况下，生成既具有低旁瓣性能又具有灵活带宽的随机雷达信号。

3 仿真结果

通过数值仿真验证了设计的随机雷达信号的性能。脉冲宽度为 20 微秒，设计带宽为 40 兆赫兹，采样频率为 300 兆赫兹。

通过上述方法可得到 6000 个采样点。众所周知，压缩随机雷达信号有两种方法，即相关法和匹配滤波法。通过将探测信号的延迟副本与目标回波信号进行相关运算，相关法可通过相关结果获得目标的距离。

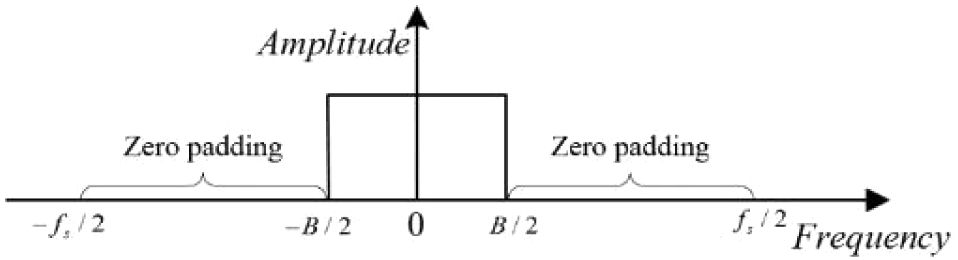
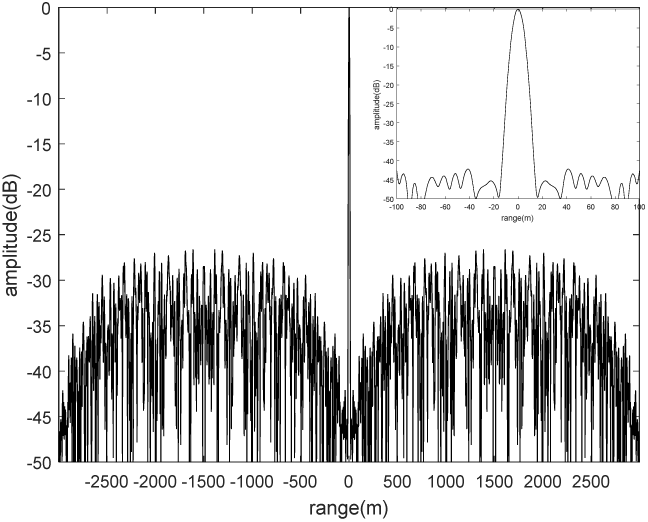
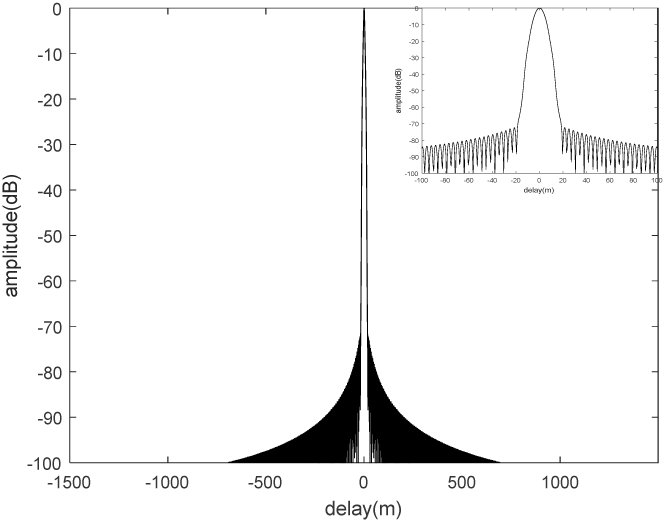
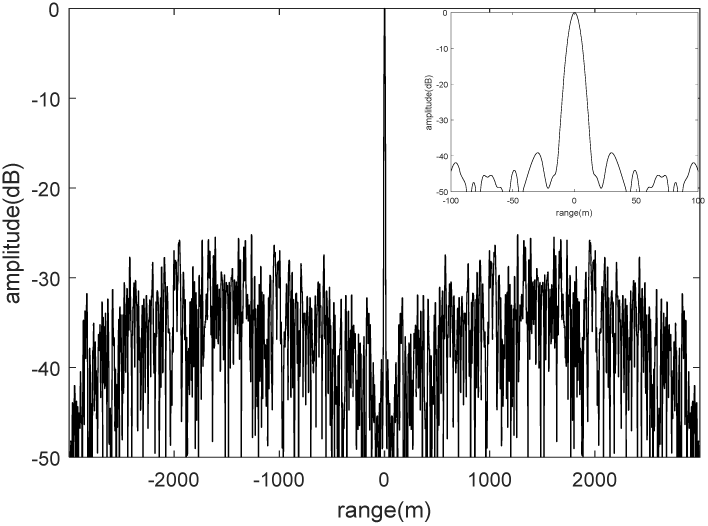
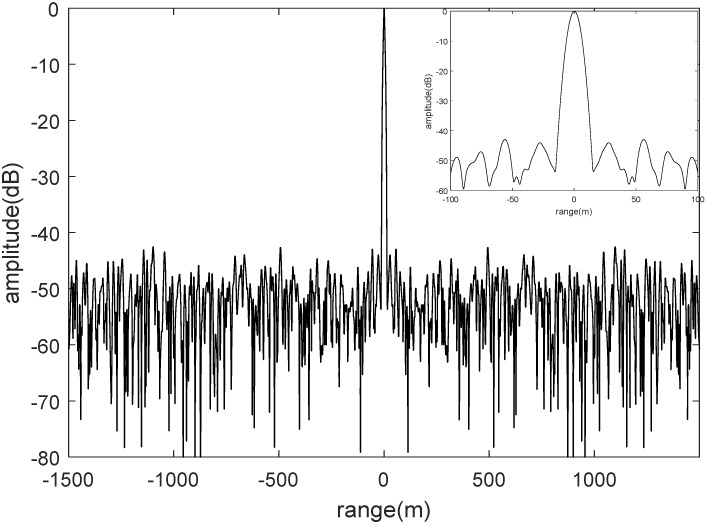
图2展示了设计的随机雷达信号的自相关结果。其自相关的峰值旁瓣比（PSLR）低于−25分贝。此外，当延迟在 [−100米，100米]范围内时，设计的随机雷达信号的相关结果低于−42分贝。然而，相关方法通常以模拟方式处理，不仅难以控制而且成本较高。而匹配滤波通常用于数字信号处理，能够更方便、高效地压缩随机雷达信号。图3展示了设计的随机雷达信号的匹配滤波输出。

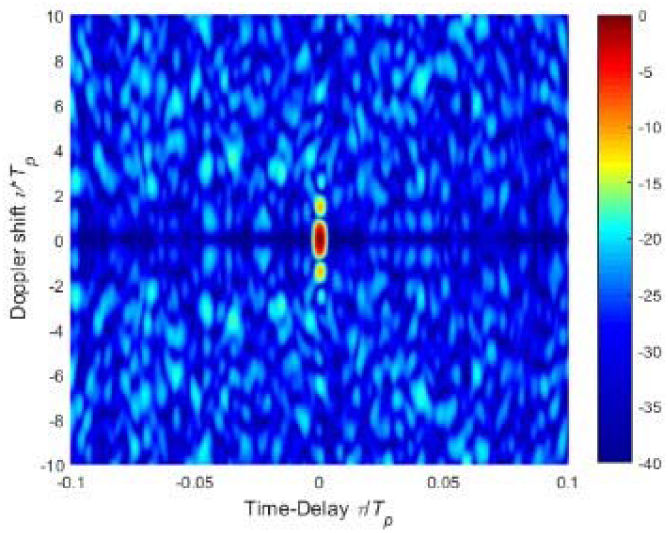
随机雷达信号的峰值旁瓣比低于−70分贝。这是因为设计的随机雷达信号的功率谱密度呈高斯形状，从而保证了低旁瓣。为了避免邻近目标的遮蔽效应，在现代雷达应用中，低旁瓣性能至关重要。比较图2和图3所示的结果可以发现，两种方法的峰值旁瓣比存在显著差异。这是因为相关等效于线性卷积运算，当延迟不为零时，部分采样点会被舍弃；而匹配滤波等效于循环卷积运算，不会丢失任何采样点。设计的随机雷达信号的模糊函数也在图4中给出。注意，设计的随机雷达信号具有类似于白高斯噪声信号的图钉状模糊函数。

如今，雷达信号通常首先以数字方式生成，然后使用数模转换器（DAC）将数字雷达信号转换为模拟信号。在实际雷达系统中，必须考虑DAC的量化效应。对于大多数高速 DAC，其量化位数通常不超过14位。因此，我们分析了在14位量化的条件下，数字实现对设计的随机雷达信号峰值旁瓣比（PSLR）的影响。此外，如图5所示，尽管具有极大振幅的采样点数量很少，但仍然存在。为了降低信号的峰均功率比，在量化过程中应对振幅进行截断。图5显示了设计的随机雷达信号实部的直方图。可以看出，该信号的直方图呈现正态分布，99%的振幅位于区间[−3δ, 3δ]内，其中 δ为标准差。因此，若将阈值设为3δ，即可保证信号的随机性。通过这种方式，可实现更高的发射效率。

4 实测数据实验

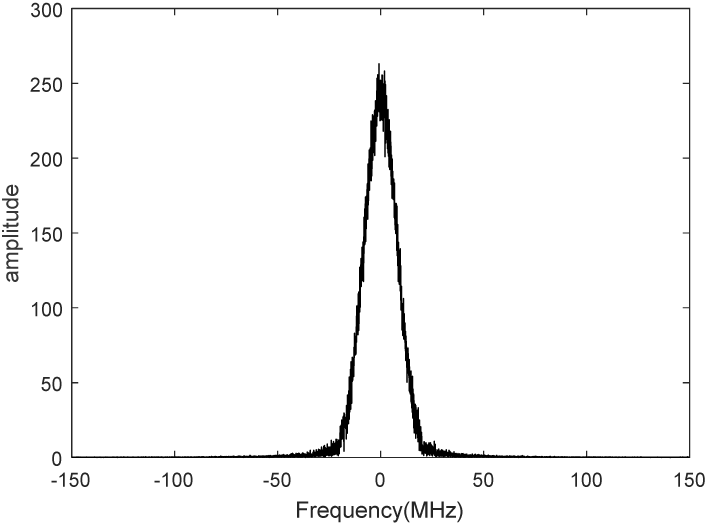
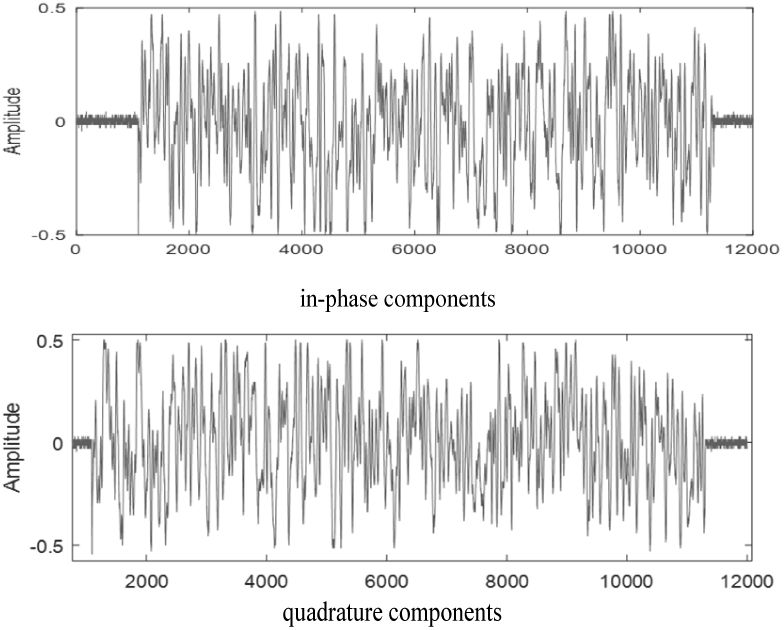
为了验证采用频域调制方法设计的随机雷达信号的低旁瓣性能，本文给出了双极化雷达系统下脉冲压缩和人体运动微多普勒特征的实验结果。在采样频率300 MHz条件下，将带宽40 MHz、持续时间20 μs的数字实现信号以14位量化精度加载至任意波形发生器中。使用8位量化精度的泰克MSO70404示波器在500 MHz采样频率下对设计的随机雷达信号进行采样和存储。随后，通过匹配滤波在数字方式下对采样的随机雷达信号进行压缩。如图9所示，采样的I/Q基带波形表现出良好的随机特性。同时给出了匹配滤波结果

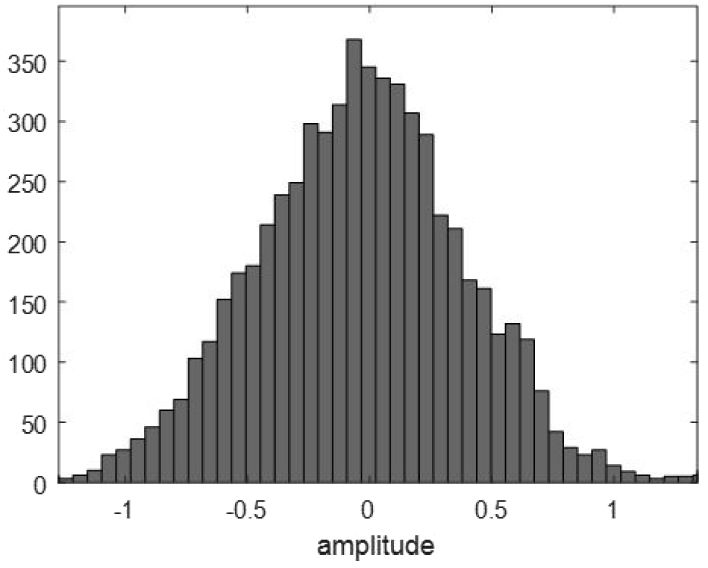
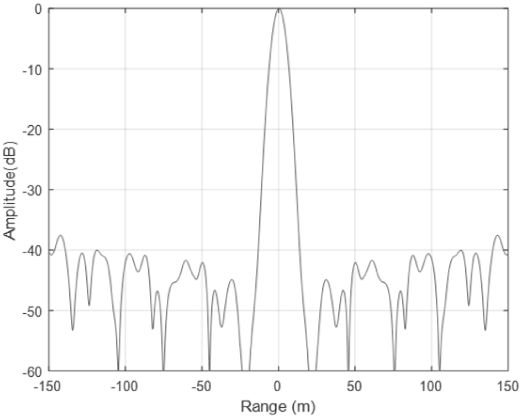
图10，在[−150 m, 150 m]范围内实现了低于−38 dB的低旁瓣。

我们发现，与仿真结果相比，实验结果的峰值旁瓣比恶化了约 4 dB，这主要是由于示波器的量化噪声（仅有8位量化精度）以及测试系统中的一些非线性失真所致。

此外，还展示了利用随机雷达信号对人体运动的极化微多普勒特征进行的实测实验。实验场地场景如图11所示。使用了两副天线：一副具有水平极化的天线用于发射脉冲随机雷达信号，另一副具有双极化的天线用于接收。本实验所用雷达为毫米波雷达，是一部Ka波段脉冲相干雷达，脉冲重复频率700 Hz。实验在室内办公室进行，一名人员站在距离雷达约3米的位置周期性地摆动手臂。

通过压缩采集的数据，可以获得人体当前姿态的高分辨率距离像（HRRP）。通过时频分析可以从高分辨率距离像（HRRP）中提取人体运动的微多普勒特征。人体运动的极化散射特性反映在谱图能量分布中。图12给出了同极化HH和交叉极化HV极化的微多普勒特征。在躯干轨迹中，交叉极化的幅度比同极化低一个数量级，且

在手臂轨迹中，交叉极化远高于同极化。这是因为静态躯干在HH极化下的雷达散射截面更大，而弯曲的手臂对HV极化更为敏感。可以看出，极化微多普勒特征包含了更多目标微动的信息，有利于目标识别的研究。

5 结论

随机信号雷达由于其随机波形，在低截获概率/低探测概率和良好的电子抗干扰能力方面具有巨大优势。然而，通用随机雷达信号存在高旁瓣问题，强回波信号容易遮蔽远距离目标的弱回波。为了减轻遮蔽效应，采用频域调制方法设计了一种具有低旁瓣性能的新型随机雷达信号。所设计的随机雷达信号因其高斯形状功率谱密度而具备低旁瓣特性，并因其随机相位谱而保持良好的随机性。数值仿真和实测数据的匹配滤波结果均验证了所设计随机雷达信号的低旁瓣性能。此外，还研究了人体运动的极化微多普勒特性。