数字图像处理 张量分解的概念、发展及其应用

一、张量的概念

        张量是一个多维数组。更正式地说，N向或N阶张量是N个向量空间的张量乘积的一个元素，每个向量空间都有自己的坐标系。张量的概念不能与物理和工程中的张量（如应力张量）混淆，后者在数学中通常被称为张量场。三阶张量如下图所示。一阶张量是向量，二阶张量是矩阵，三阶或更高阶的张量称为高阶张量。

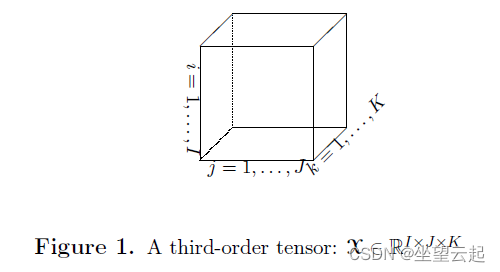
        张量（多维数组）作为向量和矩阵的高阶泛化，可以充分揭示多关系或多模态数据背后的内在结构信息。例如，受多种条件影响的面部图像集合可以表示为四阶张量，其维数为像素×人×姿势×照明。这种基于张量的表示从更高阶的角度更好地理解了信息背后的关系。

        张量在许多应用中发挥着重要作用，如信号处理、机器学习、生物医学工程、神经科学、计算机视觉、通信、心理测量学和化学计量学。它们可以为制定和解决这些领域的问题提供一个简明的数学框架。

        以下是一些涉及张量框架的案例：

 &