六、线性规划 两阶段单纯形法

最新推荐文章于 2025-03-25 23:09:44 发布
最新推荐文章于 2025-03-25 23:09:44 发布
阅读量3k 收藏 1
点赞数 1
CC 4.0 BY-SA版权
分类专栏： 深度学习从入门到精通 文章标签： 两阶段单纯形法 运筹学 线性规划 最优解 约束条件
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.youkuaiyun.com/bashendixie5/article/details/124697931
本文详细介绍了两阶段单纯形法在解决线性规划问题中的应用。首先通过辅助问题确定原始线性规划的可行性，然后从基本可行解出发求得最优解。文章通过具体的例子展示了如何设置单纯形表并解决线性规划，讨论了线性程序不可行时的处理方法以及在处理松弛变量时的优化技巧。

摘要生成于 C知道 ，由 DeepSeek-R1 满血版支持， 前往体验 >

1、要解决的问题

        当我们的可行域有形式{Ax \leq b, x \geq 0}，并且b \geq 0，我们添加的松弛变量以将程序置于等式形式形成我们的起始基础。也就是说，当要求我们所有的变量都是非负的，并且点x=0是可行的，就是一个基本可行的解。

        假设我们有这样一个问题：

        

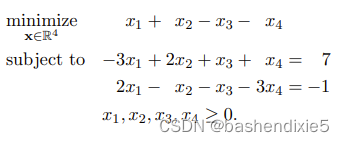
        我们按理应该绝对可以用单纯形法解决这个问题。前提是我们有一个基本可行的解决方案。

我们可以尝试猜测：尝试看看以x1和x2为基本变量的基本解是否可行。如果不可行，请尝试x1和x3，依此类推。但是我们不一定知道这个线性程序有任何可行的解决方案，这样尝试不是

了解本专栏 订阅专栏 解锁全文
线性规划的解法：两阶段单纯形法
loop_syntax648的博客
09-23 1076
其中，c₁, c₂, …, cₙ 是目标函数中的系数；A₁₁, A₁₂, …, Aₘₙ 是约束条件中的系数；线性规划是一种数学优化方法，用于在给定的约束条件下，求解线性目标函数的最优解。本文将详细介绍两阶段单纯形法的原理，并提供相应的源代码示例。迭代过程中，根据当前基的选择，计算出基变量的解，然后计算出目标函数的值。通过求解辅助线性规划问题，得到初始基可行解，即满足所有约束条件的解。最大化：Z = c₁x₁ + c₂x₂ + …基于初始基可行解，利用单纯形法逐步迭代求解原始线性规划问题。
利用单纯形法进行线性规划求解
Metaphysicist的博客
01-24 4247
在最优化原理中，利用单纯形法线性规划问题的例题与代码例程。
两阶段单纯形法Two-phase simplex method
qq_39840694的博客
03-28 2239
我们的首要任务是使它们为零，这样我们就可以把它们从问题中去掉，然后在一个基本可行系统上继续用单纯形法。其中x3 =x4 = 0为新的非基变量，x1 = 7/5, x2 = 4/5为基变量，接下来进入阶段二。在实践中，无界问题几乎总是由不正确的公式造成的，因为无限的利润在现实中是不存在的。我们使x1 = x2 = 0来求基本可行解，此时x3 = -5，x4 = -3。设置一个单纯形表，为了做到这一点，我们用除z行以外的(1)(2)中的。在实践中，这对应的问题是要求的需求太多，这在应用程序中非常常见。
单纯形法之两阶段法
最新发布
m0_53605808的博客
03-25 803
阶段一：构造并求解辅助问题，消除人工变量，从而获得原问题的初始基本可行解。通过构造目标函数，使得只要存在满足原约束的解，辅助问题的最优值必为 0。阶段二：利用第一阶段的解构造原问题的单纯形表，开始求解原问题。在这一阶段，人工变量被剔除，目标函数变回原始目标，然后继续利用单纯形法的换基操作寻找最优解。
线性规划问题及单纯形法-两阶段法
haxixihaha的博客
10-07 8630
两阶段法 两阶段法：用计算机处理数据时，只能用很大的数代替M，可能造成计算机上的错误，这个M无法确定，故采用两阶段法，和大M法是一致的。 第一阶段：在原线性规划问题中加入人工变量，使其目标函数值为人工变量之和，且取极小值。 minw = x6+x7 因为x6>=0，x7>=0，那么w=0的话，那么x6=0，x7=0，所以有可行解。其实，引入x6和x7的目的是为了得到单位矩阵 第二阶段：在第一阶段的最终表中，去掉人工变量所在列，将目标函数的系数换成原问题的目标函数值系数，继续迭代。 例题： 第一阶
两阶段法和单纯形法
04-10
庞海藏-运筹学-两阶段法和单纯形法.
Python求解线性规划问题-两阶段法实现的单纯形法
05-09
Python求解线性规划问题_两阶段法实现的单纯形法，包括.py和.ipynb两种格式，用Jupyter Notebook打开.ipynb或者用Python软件打开.py都可成功运行，压缩包中包括测试数据，代码可输出唯一解，无穷多解，无界解，无解...
最优化-线性规划单纯形法-大M法和两阶段法程序实现.rar
06-14
其中twophase.m函数是利用两阶段单纯形法。MySimplex_method.m函数是利用大M法单纯形法求解。 MySimplex_method.m函数既包含大M法，也包含单纯形法。twophase.m的单纯形法求解是通过调用MySimplex_method.m函数实现...
两阶段单纯形法的Matlab实现
12-28
两阶段单纯形法是线性规划问题的一种求解方法，主要应用于解决有约束的最大化或最小化问题。在数学优化领域，它是最为经典且广泛使用的算法之一。本项目通过Matlab语言实现了这一算法，使得用户能够方便地输入参数并...
两阶段法求解线性规划
10-11
完整的两阶段法，程序可完美下载，熟悉单纯形算法和两阶段算法，并会使用两种算法求解线性规划问题，内有例题
matlab写的单纯形法二阶段法，大M法，灵敏度分析
08-15
matlab编写的单纯形法，其中有二阶段法，大M法，灵敏度分析
线性规划的单纯形法6_两阶段法.ppt
04-10
两阶段法-线性规划的单纯形法6_两阶段法.ppt
四.单纯形法（两阶段和大M法）
热门推荐
TaiChiChen的专栏
06-06 4万+
两阶段法   单纯形法三要素： 初始基本可行解，解的迭代，最优性检验 后两个已解决,现考虑如何获得一个初始基可行解.   我们考虑具有标准形式的线性规划问题     两阶段的第一阶段就是用单纯形法消去人工变量，即把人工变量变成非基变量，第二阶段就是从基本可行解出发用单纯形法求线性规划最优解。   用一个简单的例子来展示其过程： 大M法—
线性规划两阶段求解方法
程序猿视角
02-10 1万+
百度百科给了下面一个例子，感觉其解法不容易看明白原理，换一种解释方法，应该很容易看明白两阶段法的原理。 问题： maxz=−3x1+x3 max z = -3x_1+x_3 maxz=−3x1​+x3​ s.t. {x1+x2+x3+x4=4−2x1+x2−x3−x5=13x2+x3=9x1,x2,x3,x4,x5≥0 \left\{ \begin{array}{} x_1+x_2+x_3...
单纯形法；大M法；两阶段法
weixin_45216861的博客
09-07 1万+
可行解：满足约束条件和非负约束的解。最优解：可行解中使目标函数达到最大值的解。基本解：令非基变量为0，再求线性方程组得到的唯一解。基本可行解：满足非负约束的基本解。
两阶段法求解线性规划求解
10-26 9507
用两阶段法求解min f=2x1-x2+x3 s.t x1+2x2- x3=1     2x1+ x2+ x3=5     x1- x2+2x3=4     xi>=0,i=1,2,3 引入人工变量x4,x5,x6,使min g=x4+x5+x6s.t x1+2x2-x3+x4=1    2x1+x2+x3+x5=5    x1-x2+2x3+x6=4    xi>=0,i=1,...,6其单纯形
初始解----两阶段的单纯形法
weixin_43840538的博客
04-10 1万+
步骤： 两阶段法当然是分为两阶段了 第一阶段： 1.找出秩的个数，（秩的个数看有几行约束条件，有几行就是几个秩）增加相应个数的人工变量，得到辅助问题LP； 2.列出行列式 从上至下依次是 目标函数，辅助函数，约束条件 （目标函数要按照 比如 z = 5x1 + 21x3 ====> 0z - 5x1-21*x3,，然后根据系数填入)； 3.然后化为典式，不断进基离基，进基离基，最后找到原辅...
两阶段法（基本原理+例题解析）
m0_61209712的博客
11-16 2127
基本思想：构造一个辅助线性规划问题（ALP）,通过求解它得到线性规则（LP）的初始可行基。
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包

打赏作者

坐望云起

如果觉得有用，请不吝打赏

¥1 ¥2 ¥4 ¥6 ¥10 ¥20
扫码支付：¥1
获取中
扫码支付

您的余额不足，请更换扫码支付或充值

打赏作者

实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值