LeetCode10-正则表达式匹配
10. 正则表达式匹配:
给你一个字符串 s 和一个字符规律 p,请你来实现一个支持 ‘.’ 和 ‘*’ 的正则表达式匹配。
- ‘.’ 匹配任意单个字符
- ‘*’ 匹配零个或多个前面的那一个元素
所谓匹配,是要涵盖 整个 字符串 s的,而不是部分字符串。
示例 1:
输入:s = "aa" p = "a"
输出:false
解释:"a" 无法匹配 "aa" 整个字符串。
示例 2:
输入:s = "aa" p = "a*"
输出:true
解释:因为 '*' 代表可以匹配零个或多个前面的那一个元素, 在这里前面的元素就是 'a'。因此,字符串 "aa" 可被视为 'a' 重复了一次。
示例 3:
输入:s = "ab" p = ".*"
输出:true
解释:".*" 表示可匹配零个或多个('*')任意字符('.')。
示例 4:
输入:s = "aab" p = "c*a*b"
输出:true
解释:因为 '*' 表示零个或多个,这里 'c' 为 0 个, 'a' 被重复一次。因此可以匹配字符串 "aab"。
示例 5:
输入:s = "mississippi" p = "mis*is*p*."
输出:false
提示:
- 0 <= s.length <= 20
- 0 <= p.length <= 30
- s 可能为空,且只包含从 a-z 的小写字母。
- p 可能为空,且只包含从 a-z 的小写字母,以及字符 . 和 *。
- 保证每次出现字符 * 时,前面都匹配到有效的字符
解题思路1:
动态规划,三步走:
1.状态表示:
用dp[i][j]表示s[0i-1]和p[0j-1]是否匹配。
2.初始化:
- dp[0][0]=1
- dp[i][0]=0,i为1~n,因为s前i个字符无法匹配p0个字符
- dp[0][j]=0当p[j-1]!=’ * ‘; dp[0][j]=dp[0][j-2]当p[j-1]==’ * ’
3.状态转移:
如果 p 的第 j 个字符是一个小写字母,那么我们必须在 s 中匹配一个相同的小写字母,即
如果 p 的第 j 个字符是 *,那么就表示我们可以对 p 的第 j-1个字符匹配任意自然数次。在匹配 0 次的情况下,我们有
在匹配 1,2,3, ⋯ 次的情况下,类似地我们有
则代码如下
class Solution {
public:
bool isMatch(string s, string p) {
int n=s.size(),m=p.size();
int dp[20][30];
dp[0][0]=1;
for(int i=1;i<=n;i++)
dp[i][0]=0;
for(int j=1;j<=m;j++)
{
if(p[j-1]!='*')
dp[0][j]=0;
else
dp[0][j]=dp[0][j-2]; //*号匹配0个字符
}
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
if(p[j-1]=='.')
dp[i][j]=dp[i-1][j-1];
else if(p[j-1]=='*')
{
dp[i][j]=dp[i][j-2]; //*号匹配0个字符
char x=p[j-2];
for(int k=i-1;k>=0;k--) //*号匹配一个或者多个字符
{
if(x=='.') //如果之前是.,则任意匹配
{
dp[i][j]|=dp[k][j-2];
}
else if(x==s[k]) //相等就可以匹配多个
{
dp[i][j]|=dp[k][j-2];
}
else //不相等就无法继续匹配
break;
}
}
else
{
if(s[i-1]==p[j-1])
dp[i][j]=dp[i-1][j-1];
else
dp[i][j]=0;
}
}
}
/*for(int i=0;i<=n;i++)
{
for(int j=0;j<=m;j++)
{
printf("dp[%d][%d]=%d\n",i,j,dp[i][j]);
}
}*/
return dp[n][m];
}
};
优化:
在状态转移过程中,通过枚举进行了多次匹配,但这是真的需要的吗?
我们不妨换个角度思考:
字母+*的组合,本质上只有两种情况:
(1)匹配0次字符,dp[i][j]=dp[i][j-2]
(2)匹配多次字符,匹配成功一次就将s[i]扔掉,则状态转移方程为:dp[i][j]|=dp[i-1][j]
字母为.的情况,则一定能够匹配成功:
dp[i][j]=dp[i-1][j-1]
最终状态转移方程为:
代码如下:
class Solution {
public:
bool isMatch(string s, string p) {
int n=s.size(),m=p.size();
int dp[20][30];
dp[0][0]=1;
for(int i=1;i<=n;i++)
dp[i][0]=0;
for(int j=1;j<=m;j++)
{
if(p[j-1]!='*')
dp[0][j]=0;
else
dp[0][j]=dp[0][j-2]; //*号匹配0个字符
}
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
if(p[j-1]=='*')
{
dp[i][j]=dp[i][j-2];//匹配0个字符
if(p[j-2]=='.'||p[j-2]==s[i-1])
dp[i][j]|=dp[i-1][j]; //匹配一个或者多个
}
else if(p[j-1]=='.')
{
dp[i][j]=dp[i-1][j-1];
}
else
{
if(s[i-1]==p[j-1])
dp[i][j]=dp[i-1][j-1];
else
dp[i][j]=0;
}
}
}
return dp[n][m];
}
};





 本文介绍LeetCode上的正则表达式匹配问题,探讨如何使用动态规划解决支持'.'和'*'的正则表达式匹配问题,并提供详细的解题思路及优化后的代码实现。
本文介绍LeetCode上的正则表达式匹配问题,探讨如何使用动态规划解决支持'.'和'*'的正则表达式匹配问题,并提供详细的解题思路及优化后的代码实现。
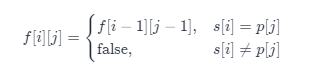
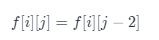
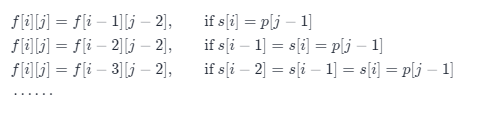
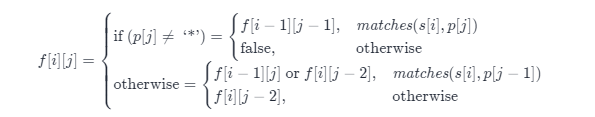
















 4687
4687

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








