天津理工大学2021编译原理期末考试复习

最新推荐文章于 2023-11-09 23:09:04 发布

扎克蕉

最新推荐文章于 2023-11-09 23:09:04 发布

阅读量1.8k

点赞数 6

分类专栏：大学课程文章标签：编译器交叉编译

本文链接：https://blog.youkuaiyun.com/banana_xray/article/details/118364117

版权

大学课程专栏收录该内容

9 篇文章

订阅专栏

说明：期末不知道复习了个啥，只会做题，还做不对，建议要考研的同学用这门课的时间复习高数，不要浪费时间！

最左推导与最右推导

每一步替换最左边非终结符。

每一步替换最右边非终结符。

示例：

现有文法G[E]:
E->E+T|E-T|T
T->T*F|T/F|F
F->(E)|i

句型(F+i)-T*(E-T)

最左推导：
E->E-T
->T-T
->F-T
->(E)-T
->(E+T)-T
->(T+F)-T
->(F+i)-T
->(F+i)-T*F
->(F+i)-T*(E)
->(F+i)-T*(E-T)

短语

定义

一个句型的语法树中任一子树叶节点所组成的符号串。

理解

其实就是找叶子节点的组合，一层层往上分析。

直接短语

在找到短语的基础上，找节点（该节点往下只有一层，没有更下子树），那么该节点的孩子就是直接短语。

句柄

最左边的直接短语。

素短语

是一个短语，至少包含一个终结符，且不含有其他素短语。

参考：https://www.bilibili.com/read/cv8492761/

正规式

不太理解定义，会做题就行。

例1：设有L(G)={a^(2n+1)b(2m)a^(2p+1)|n≥0,p≥0,m≥1}

根据这个方程，可以知道：

第一个a的幂最少是1，且为奇数 -> a(aa)*

b的幂最少是2，且为偶数 -> bb(bb)*

第三个a的幂最少是1，且为奇数 -> a(aa)*

因此正规式为a(aa)*bb(bb)*a(aa)*

总结：这时你可以看出来，*大概是通配符的意思，对应个数即可。

例2：有语言L={w|w∈(0,1)+}，并且w中至少有两个1，又在任何两个1之间有偶数个0

其实和例1很像，先把确定存在的写下来，然后加通配符。

0*1(00(00)*1)*00(00)*10*

例3（最可能考）：设有正规文法G：

Z -> 0A

A -> 0A | 0B

B -> 1A | ε

第一步：用+替代|，=替代-> ，得到结果：

Z = 0A (1)

A = 0A + 0B (2)

B = 1A + ε (3)

(3)代入(2)得：A=0A+01A+0 (4)

对(4)分配律得：A=(0+01)A+0 (5)

对(5)求解规则得：A=(0+01)*0 (6)

将(6)带入(1)，得：Z=0(0+01)*0

则正规式为R=0(0|01)*0

总结：要熟记求解规则：

若 x = αx | β (或 x = αx + β ) 
则解为 x = α*β; 
若 x = xα | β (或 x = xα + β ) 
则解为 x = βα *  
以及正规式的分配律、交换律和结合律求关于文法开始符号的正规式方程组的解。

NFA（注意R+）

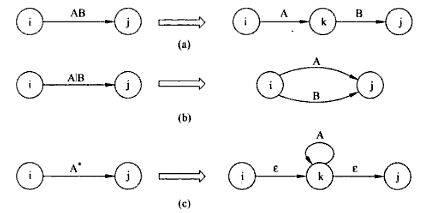
DFA

用子集法通过NFA确定化为DFA，习题参考P6

最小化：https://www.zhihu.com/question/39767421

DAG优化

https://www.bilibili.com/video/BV1aT4y1J7Qp?from=search&seid=11787537104224591425

FIRST集

理解

FIRST(A)是以A开始符的集合，A的所有可能推导的开头终结符或是ε

1.后面跟的不是非终结符（大写字母）

...
A->aB|ε
A->c
...
First(A)={a，ε，c}

2.后面跟非终结符-情况①

...
A->Ba
B->b
...
First(A)={b}

3.后面跟非终结符-情况②

...
A->Bc
B->b|ε
...
First(A)={b,c}

4.后面跟非终结符-情况③

...
A->BC
B->b|ε
C->c|ε
...
First(A)={b,c,ε}

FOLLOW集

理解

Follow(A)为非终结符A后跟符号的集合,Follow(A)是所有句型中出现在紧接A之后的终结符或’#’

规则

（1）对于文法的开始符号S,置#于Follow（S）中；

（2）若A->αBβ是一个产生式，则把First(β) \ {ε} 加入到Follow（B）中

（3）若A->αB是一个产生式，或A->αBβ是一个产生式且β=>ε，则把Follow(A)加入到Follow(B)中

例题1

G(S)：S->IETSP|O
I->if
E->b
O->other
L->else
T->then
P->LS|ε

求解

FIRST	FOLLOW
First(S)={if,other}	FOLLOW(S)={else,#}
First(I)={if}	FOLLOW(I)={b}
First(E)={b}	FOLLOW(E)={then}
First(O)={other}	FOLLOW(O)={else,#}
First(L)={else}	FOLLOW(L)={if,other}
First§={else,ε}	FOLLOW§={else,#}
First(T)={then}	FOLLOW(T)={if,other}

总的来说，FOLLOW集找箭头右边的字母，看后面还有没有字母，如果有根据规则2（加后一个字母的FIRST集减去空集）,如果后面字母能推出空，还要走规则3。没有则根据规则3（加箭头左边字母的FOLLOW集）。

个人疑惑：A->aBβC ，若β能推出空，那么FOLLOW(B)肯定是FIRST(β)/空+FIRST©/空，如果C也能推出空，才把FOLLOW(A)加进FOLLOW(B)。就是存在B后面都能为空的情况，才把FOLLOW(A)加进去。（猜测）

例题2（实验题）

E->E+T|E-T|T
T->T*F|T/F|F
F->P^F|P
P->(E)|i

非终结符有

E T F P

终结符有

+ - * / ^ ( ) i

预测分析表

习题解析P24

FIRSTVT集

找Firstvt的三条规则：

如果要找A的Firstvt，A的候选式中出现：
A->a…，即以终结符开头，该终结符入Firstvt
A->B…，即以非终结符开头，该非终结符的Firstvt入A的Firstvt
A->Ba…，即先以非终结符开头，紧跟终结符，则终结符入Firstvt

LASTVT集

**找Lastvt的三条规则：**如果要找A的Lastvt，A的候选式中出现：
A->…a，即以终结符结尾，该终结符入Lastvt
A->…B，即以非终结符结尾，该非终结符的Lastvt入A的Lastvt
A->…aB，即先以非终结符结尾，前面是终结符，则终结符入Lastvt

算符优先顺序表

https://blog.youkuaiyun.com/qq_37977106/article/details/80301761

参考

改造LL1文法

P25

消除左递归：课本P49

重要公式：

A -> Aα|β
消除后：
A -> βA'
A' -> αA'| ε

消除回溯：课本P51

重要公式（提取左公因式）：

A -> δβ1|δβ2|...|βi+1|...|βj
消除后：
A -> δA'|βi+1|...|βj
A' -> β1|...|βj

例子：
G'[A]: A->aAB|a|b
消除后：
G'[A]: A->aA'|b
A'-> AB|ε

构造识别活前缀的DFA、分析表

课本P82