目录
- 总结
- 1、交换元素swap
- 2、链表设置哑结点
- 3、while(cur -> next != nullptr)代表运行到倒数第二个元素,也就是cur此时为倒数第一个元素
- 4、在cur初始指向哑结点时,下面执行cur指向index的前一个节点
- 5、关于链表,什么移动删除元素等,多创建节点指向,别一个节点的next,next的next,而且命名时用题目给的
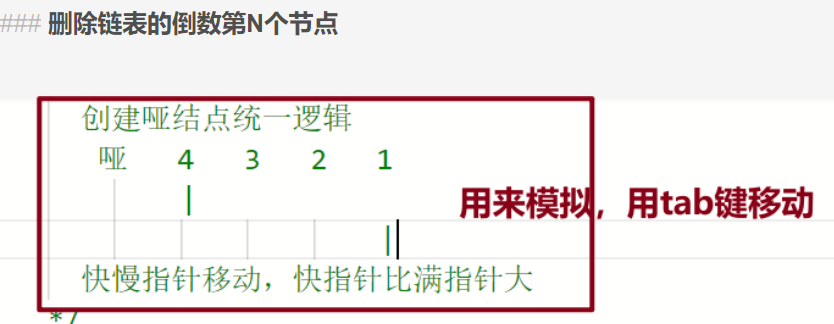
- 6、用tab键模拟运行
- 7、二分的循环最后一次一定是处在left = right状态
- 8、vector不初始化,不能在下面直接vector[0]进行访问,注意!!!!!!!
- 9、务必进行初始化
- 10、最大滑窗和最小滑窗模板
- 查看unordered_map的遍历 auto a : mp,a是迭代器(可能是),但是指向second直接用的点
- 字符串
- 链表
- 滑动窗口
- 哈希表
- 数组
总结
1、交换元素swap
vector也能交换 swap(v[1],v[2]);
2、链表设置哑结点
统一逻辑对头结点操作
3、while(cur -> next != nullptr)代表运行到倒数第二个元素,也就是cur此时为倒数第一个元素
4、在cur初始指向哑结点时,下面执行cur指向index的前一个节点
while(–index) cur = cur -> next;
5、关于链表,什么移动删除元素等,多创建节点指向,别一个节点的next,next的next,而且命名时用题目给的
比如1-》2-》3-》4,就命名为p1 p2 p3等,这样好设计
6、用tab键模拟运行
7、二分的循环最后一次一定是处在left = right状态
最后是一个趋近的过程,left和right的平均值最后趋于不动,这时候,left可能向右走,可能right向左走,这时候一定一定有规律。
8、vector不初始化,不能在下面直接vector[0]进行访问,注意!!!!!!!
要添加元素后,有元素后才能下标访问,也就是必须push_back()后
9、务必进行初始化
数进行循环判断出错了!!!!
10、最大滑窗和最小滑窗模板
最小滑窗
while j < len(nums):
判断[i, j]是否满足条件
while 满足条件:
不断更新结果(注意在while内更新!)
i += 1 (最大程度的压缩i,使得滑窗尽可能的小)
j += 1
最大滑窗
while j < len(nums):
判断[i, j]是否满足条件
while 不满足条件:
i += 1 (最保守的压缩i,一旦满足条件了就退出压缩i的过程,使得滑窗尽可能的大)
不断更新结果(注意在while外更新!)
j += 1
左窗口一个是满足了就退出,让右窗口接着走,每次走一步
左窗口一个是满足了继续压缩,让右窗口去满足条件,这时候右窗口可能走几步
查看unordered_map的遍历 auto a : mp,a是迭代器(可能是),但是指向second直接用的点
字符串
1、移除元素
给你一个数组 nums 和一个值 val,你需要 原地 移除所有数值等于 val 的元素,并返回移除后数组的新长度。
我觉得可以遇到后,将当前元素与最后一个元素对换,但是判断有点麻烦
双指针法
快指针:寻找新数组的元素 ,新数组就是不含有目标元素的数组
慢指针:指向更新 新数组下标的位置

2、反转字符串
编写一个函数,其作用是将输入的字符串反转过来。输入字符串以字符数组 char[] 的形式给出,,使用 O(1) 的额外空间
输入:[“h”,“e”,“l”,“l”,“o”]
输出:[“o”,“l”,“l”,“e”,“h”]
双指针

3、替换空格
把字符串 s 中的每个空格替换成"%20"。不用额外辅助空间
示例 1: 输入:s = “We are happy.”
输出:“We%20are%20happy.”
换了以后就修改了结构,如何知道位置
先统计空格的个数,计算需要的总长度 ,然后将字符串扩展,快慢指针从扩展的字符串后面开始遍历。

4、翻转字符串里的单词
这个是翻转单词,空间复杂度要求为O(1)。输入字符串 s中可能会存在前导空格、尾随空格或者单词间的多个空格。
输入: “the sky is blue”
输出: “blue is sky the”
不解:我是三个字母,另外是四个字母,那这怎么替换
用下面方法,举个例子,源字符串为:"the sky is blue "(blue后面有个空格)
移除多余空格 : “the sky is blue”
字符串反转:“eulb si yks eht”
单词反转:“blue is sky the”
5、反转链表
6\三数之和为0
三数之和为0
输入:nums = [-1,0,1,2,-1,-4]
输出:[[-1,-1,2],[-1,0,1]]

链表
链表——构建
// 单链表
struct ListNode {
int val; // 节点上存储的元素
ListNode *next; // 指向下一个节点的指针
ListNode(int x) : val(x), next(NULL) {} // 节点的构造函数
};
1、删除链表中等于给定值 val 的所有节点。

2、链表——设计链表的各个操作函数
get(index):获取链表中第 index 个节点的值。如果索引无效,则返回-1。
addAtHead(val):在链表的第一个元素之前添加一个值为 val 的节点。插入后,新节点将成为链表的第一个节点。
addAtTail(val):将值为 val 的节点追加到链表的最后一个元素。
addAtIndex(index,val):在链表中的第 index 个节点之前添加值为 val 的节点。如果 index 等于链表的长度,则该节点将附加到链表的末尾。如果 index 大于链表长度,则不会插入节点。如果index小于0,则在头部插入节点。
deleteAtIndex(index):如果索引 index 有效,则删除链表中的第 index 个节点。
3、反转链表
输入: 1->2->3->4->5->NULL 输出: 5->4->3->2->1->NULL
注意这个题是头插法 ,找到头后,从头后面插

整整真正的做法

两两交换链表中的节点


删除链表的倒数第N个节点

链表相交

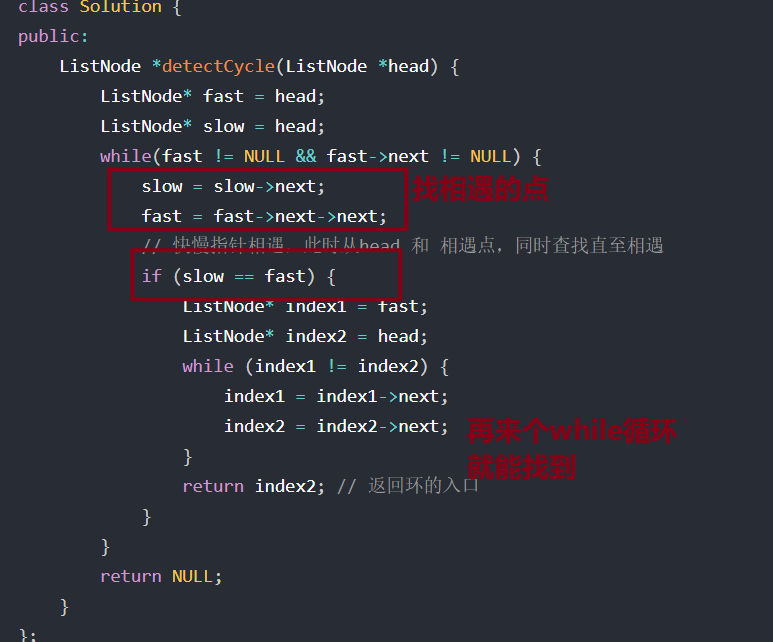
环形链表II
fast走两步,low走一步
fast指针一定先进入环中,如果fast指针和slow指针相遇的话,一定是在环中相遇

为什么一定相遇 ,fast是走两步,slow是走一步,其实相对于slow来说,fast是一个节点一个节点的靠近slow的
公式计算的详细过程
结论是快指针走两步,慢指针走一步,找到它们相遇的地方,然后从这个地方和头结点一起发出一个速度一样的指针 ,然后再相遇的节点就是环形入口
1、二分查找
这里有两种写法,还是按传统 的写法,结束寻找是left>right,也就是while循环里的判断条件是left<=right,每次判断mid,大了向左走,小了向右走,等于就返回。

1)搜索插入位置
如果找到返回位置,找不到在合适的位置插入
可以直接从头开始找,暴力,但O(n)
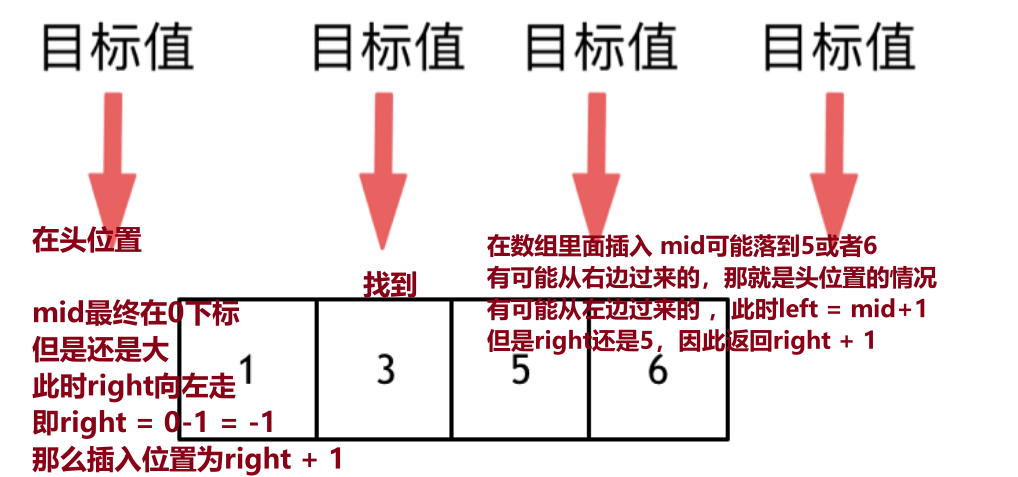
还是二分,插入位置返回right+1
2)在排序数组中查找元素的第一个和最后一个位置
输入:nums = [5,7,7,8,8,10], target = 8
输出:[3,4]
也就是返回目标值的返回,没找到返回[-1,-1]
用两个二分法找左右边界值

设立的如果mid当前值大了,会让right向左移动

上面求到的右边界是右边界+1。具体过程是让right不断趋近右边界直到等于右边界或者右边界+1,而mid在判断中,不断赶着left向右移动,直到最后left和right的平均值等于在右边界或者右边界第一个元素,总之是left跟着mid不断趋近右边界的过程,每次用个变量存储left的位置,随着位置的趋近,最后停在右边界右边第一个位置,然后while退出。
同理找到左边界-1
处理时有两种情况,一种是找到,一种是没找到,没找到在数组之外,或者在数组之内,只是没有这个数,没找到前者有一个返回-2,另一种是俩边界相等。

3)x 的平方根
输入:x = 4
输出:2
也就是从1到x二分找数的平方。

这样最终有两种结束条件的情况,

但是上面这样写的话会超时,考虑到除了1,x开平方都是小于x的一半,针对x = 0和x= 1加个判断,让right= x /2;

但是还是超时
4)有效的完全平方数

有序数组的平方
一个非递减数组,返回其平方的有序数组
输入:nums = [-7,-3,2,3,11] 输出:[4,9,9,49,121]
负数有可能平方后就大于后面的值了,但是有一点可能把握,两边平方后一定是大的,往里是逐渐变小的。因此可以用双指针一直往里靠近。

滑动窗口
长度最小的子数组(最小滑动窗口)√
给定一个含有 n 个正整数的数组和一个正整数 s ,找出该数组中满足其和 ≥ s 的长度最小的 连续 子数组,并返回其长度。如果不存在符合条件的子数组,返回 0。
示例:
输入:s = 7, nums = [2,3,1,2,4,3] 输出:2 解释:子数组 [4,3] 是该条件下的长度最小的子数组。
这种题就是看滑动窗口的长度
不能先排序,然后左右指针,大了一点右指针向左移动,小了,左指针向右移动,因为没法启动,怎么让 左指针向右移动呢,怎么让右指针向左移动呢,后者移动后怎么结束呢。
因此应该用滑动窗口,滑动窗口保证大于等于目标值,如果小了右窗口就向右移动也就是再拿个元素,如果大了左窗口就向右移动舍去一个元素。那么这样的话,初始时都指向第一个元素,那么如果第一个元素大了怎么办,岂不是左指针就比右指针大了??? 不能仅仅满足让滑动窗口的值等于目标值,那岂不是不移动了,因此需要逼着 它,满足了或者小于了我就再加个元素


因此可以认为右窗口是一个固定的值,让左窗口拉伸伸缩。
水果成篮(最大滑动窗口 需要二刷)
大概意思就是寻找两个数,扩散的范围最大,中间不能有其它的在里面。
输入:fruits = [1,2,3,2,2]
输出:4
解释:可以采摘 [2,3,2,2] 这四棵树。
如果从第一棵树开始采摘,则只能采摘 [1,2] 这两棵树。
注意这个题的逻辑表达,如何用map来判断是否满足条件

最小覆盖子串(最小滑动窗口 需要二刷)
输入:s = “ADOBECODEBANC”, t = “ABC”
输出:“BANC”
t字符可能有重复的,比如 ABA
包含ABC,并且长度是最小的,由于是在原字符串上找,因此肯定是有左右的东西,所以大概是左右指针或者滑动窗口
这次右窗口的逻辑是直到找到满足条件的情况后才停止,那么左窗口的逻辑就是尝试往右走,符合逻辑就尝试更新最小值,直到不符合逻辑了,这时候就能驱动着右窗口往右走了。
但关键是怎么存储,
可以用一个哈希表表示 t中所有的字符以及它们的个数
用一个哈希表动态维护窗口中所有的字符以及它们的个数
如果这个动态表中包含 t 的哈希表中的所有字符,并且对应的个数都不小于 t 的哈希表中各个字符的个数,那么当前的窗口是「可行」的


螺旋矩阵II

这个循环,[),[),[),[)四个左闭右开就全连上了,一个完整的赋值循环
循环多少次,n/2,
如果是奇数怎么办,比如3,那么3/2=1,就只循环一次,单独设置最后一个元素



哈希表
哈希表基础
哈希表都是用来快速判断一个元素是否出现集合里。
有效的字母异位词
给定两个字符串 s 和 t ,编写一个函数来判断 t 是否是 s 的字母异位词
就是仅仅顺序不一样,字母组成一样
先遍历S,加入哈希表。再遍历T,从哈希表中减去。
赎金信
判断第一个字符串 ransom 能不能由第二个字符串 magazines 里面的字符构成。但是第二个字符串的每个字符只能用一次。
输入:ransomNote = “aa”, magazine = “aab”
输出:true
先遍历后者加入哈希表。再遍历第一个,减哈希表。
字母异位词分组

定义一个unordered_map,字符串为键,值为一个vector,每次对str排序,然后将值加入map

找到字符串中所有字母异位词(重要 滑动窗口加哈希表)





数组
两个数组的交集
第一个数组中有4 9 ,第二个数组里也有 9 4,就是 看都有的元素
输入:nums1 = [4,9,5], nums2 = [9,4,9,8,4]
输出:[9,4]
解释:[4,9] 也是可通过的
第一个加入哈希表,第二个加入哈希表
遍历第一个哈希表判断第二个哈希表有没有
三数之和
1、首先对数组进行排序,这是双指针法的前提条件。
2、遍历数组,对于每一个数 nums[i],我们将其作为第一个数,然后在剩下的数中使用双指针法寻找两个数,使得三个数之和等于0。
3、双指针法的具体实现如下:定义两个指针,左指针 l = i + 1,右指针 r = n - 1,其中 n 为数组的长度。每次移动左右指针,直到找到符合条件的三个数。如果三数之和小于0,则左指针向右移动一位,如果三数之和大于0,则右指针向左移动一位,否则说明找到了一个符合条件的三元组。
在遍历过程中,需要注意去重,避免输出重复的三元组。
去重有两处
i的遍历,当前i已经找到了,下一个i还一样,就跳过了
for (int i = 0; i < nums.size(); i++) {
if (i > 0 && nums[i] == nums[i-1]) continue; // 跳过相同的第一个元素
// ...
}
找到目标值了,随便移动一个指针打破结构,但是移动的这个指针需要找到下一个不一样的元素
if (nums[left] + nums[right] + nums[i] == 0)
{
result.push_back({ nums[i],nums[left],nums[right] });
do { left++; } while (left < right && nums[left] == nums[left-1]);
}

四数之和

翻转字符串
左右指针 swap函数
反转字符串 II
i每次走2k个长度,这个是一步
2k个长度,前k个反转,如果不到k了,有多少个反转多少个

处理空格
字符串前面有空格,字符串里面的单词里也可能有大于1个的空格,字符串后面也可能有空格,将其处理成正常的字符
" the sky is blue "
“the sky is blue”
这个在for和while的处理上体现了个人的代码风格

下面这种方法前闭后开,闭是指fast指向一个正常字符,开是会略过空格
为保证前闭,刚进入for要到闭那里
resize要放在外面写,否则会出现并没有resize的情况

反转字符串中的单词
使用上面的处理函数

剑指Offer 05.替换空格
请实现一个函数,把字符串 s 中的每个空格替换成"%20"。
示例 1: 输入:s = “We are happy.”
输出:“We%20are%20happy.”
先for一遍计算空格个数,快慢指针,快指针指向当前数组的最后一个,然后和慢指针配合
剑指Offer58-II.左旋转字符串
将前面几个字符挪到后面去
输入: s = “abcdefg”, k = 2
输出: “cdefgab” 这个是将ab挪到后面
不能申请额外空间
比如ABCD,翻转前两个,再反转后面的,再来个大反转
ABCD -> BACD->BADC->CDAB
KMP(用状态集好难理解)
KMP暴力匹配
// 暴力匹配(伪码)
int search(String pat, String txt) {
int M = pat.length;
int N = txt.length;
for (int i = 0; i <= N - M; i++) { //从头开始对每个字符都进行匹配
int j;
for (j = 0; j < M; j++) { //在里面开始对每个字符进行匹配
if (pat[j] != txt[i+j])
break;
}
// pat 全都匹配了
if (j == M) return i;
}
// txt 中不存在 pat 子串
return -1;
}


KMP就是一个动态规划,dp数组里面存着数据
因此给我个上面的apt,我就能计算出dp数组来,计算出dp来,如果根据这些信息移动pat的指针,那么就需要确定有限状态机来确定了,到达某个状态,遇到什么字符,确定什么行为。明确两个变量,一个是当前的匹配状态,另一个是遇到的字符,通过确定有限状态机来确定它的状态转移行为 。


确定有限自动机用二维dp数组来表示
dp[j][c] = next
0 <= j < M,代表当前的状态
0 <= c < 256,代表遇到的字符(ASCII 码)
0 <= next <= M,代表下一个状态
dp[4]['A'] = 3 表示:
当前是状态 4,如果遇到字符 A,
pat 应该转移到状态 3
所以说在创建为dp后,就能很快写出代码
public int search(String txt) {
int M = pat.length();
int N = txt.length();
// pat 的初始态为 0
int j = 0;
for (int i = 0; i < N; i++) {
// 当前是状态 j,遇到字符 txt[i],
// pat 应该转移到哪个状态?
j = dp[j][txt.charAt(i)];
// 如果达到终止态,返回匹配开头的索引
if (j == M) return i - M + 1;
}
// 没到达终止态,匹配失败
return -1;
}
关键的是在于如何构建状态转移图
for 0 <= j < M: # 状态
for 0 <= c < 256: # 字符
dp[j][c] = next
状态推进:如果遇到的字符 c 和 pat[j] 匹配的话,next = j + 1
状态重启:如果字符 c 和 pat[j] 不匹配的话,状态就要回退(或者原地不动)
而所谓的状态重启就是到和它有相同前缀的位置。
看看有相同前缀位置的地方遇到和我一样的字符能否推进,如果能推进就转移过去,如果不能推进就回退到状态
下面 状态 X 总是落后状态 j 一个状态,与 j 具有最长的相同前缀
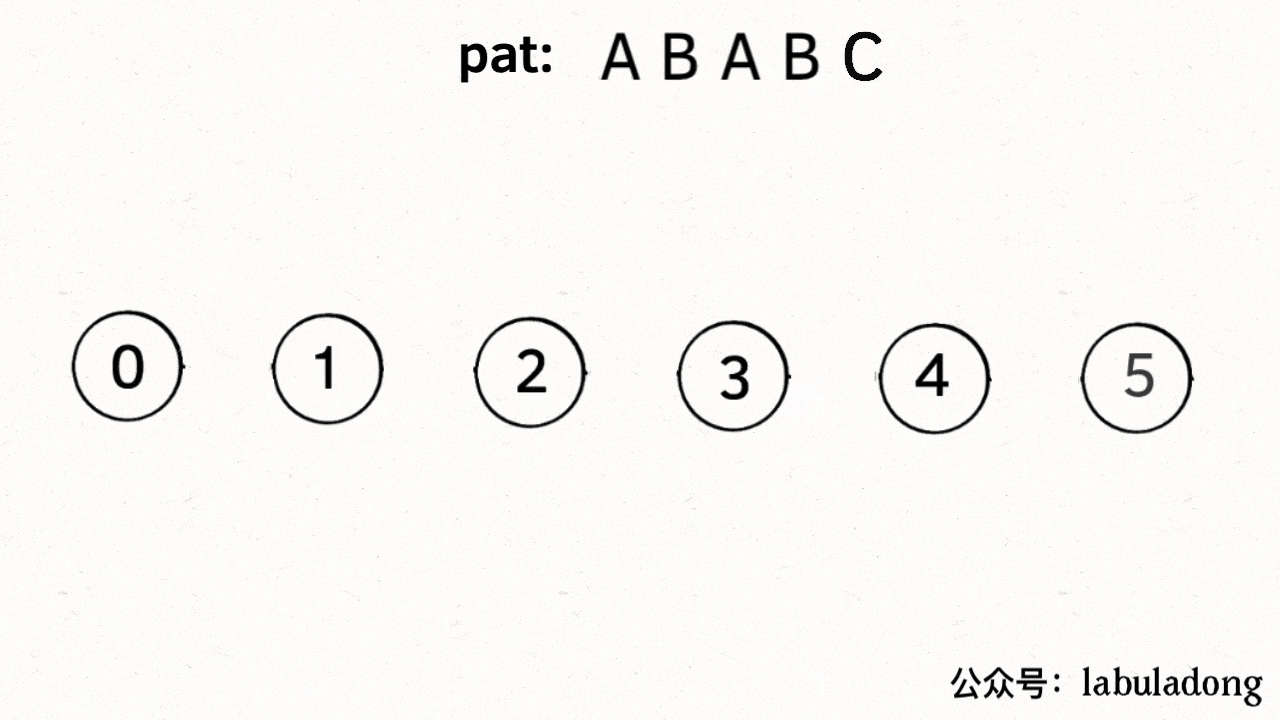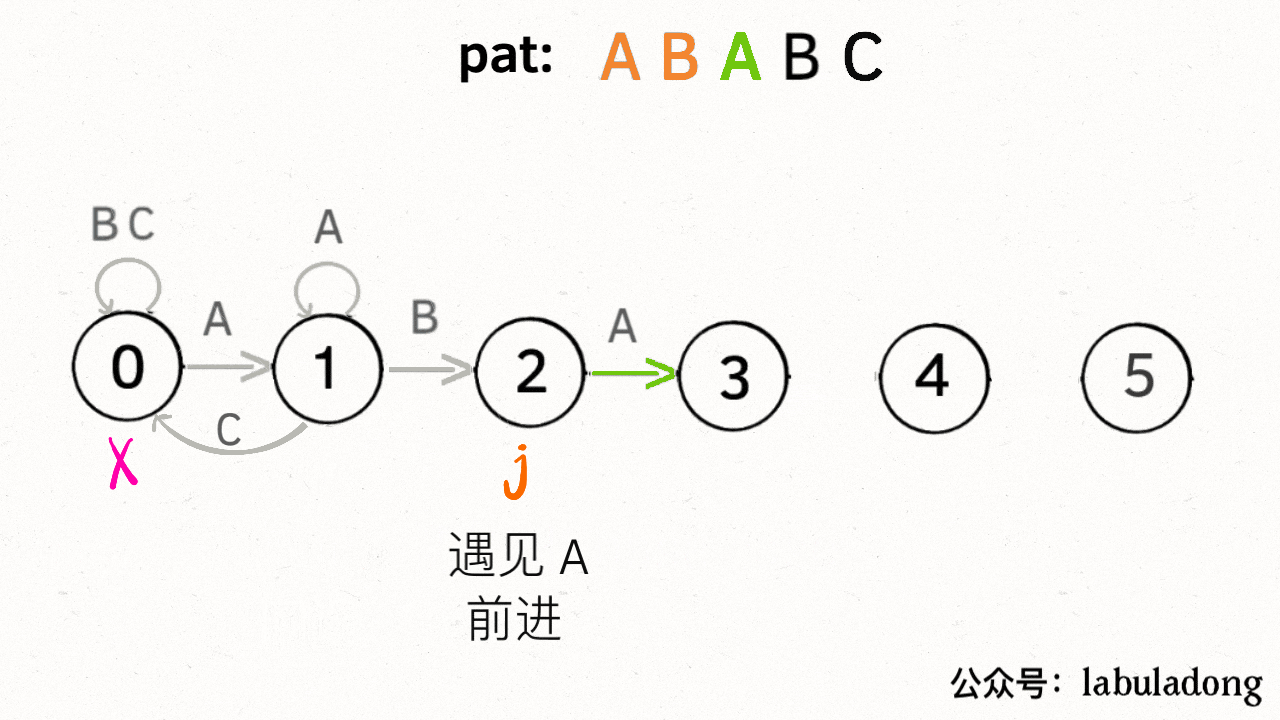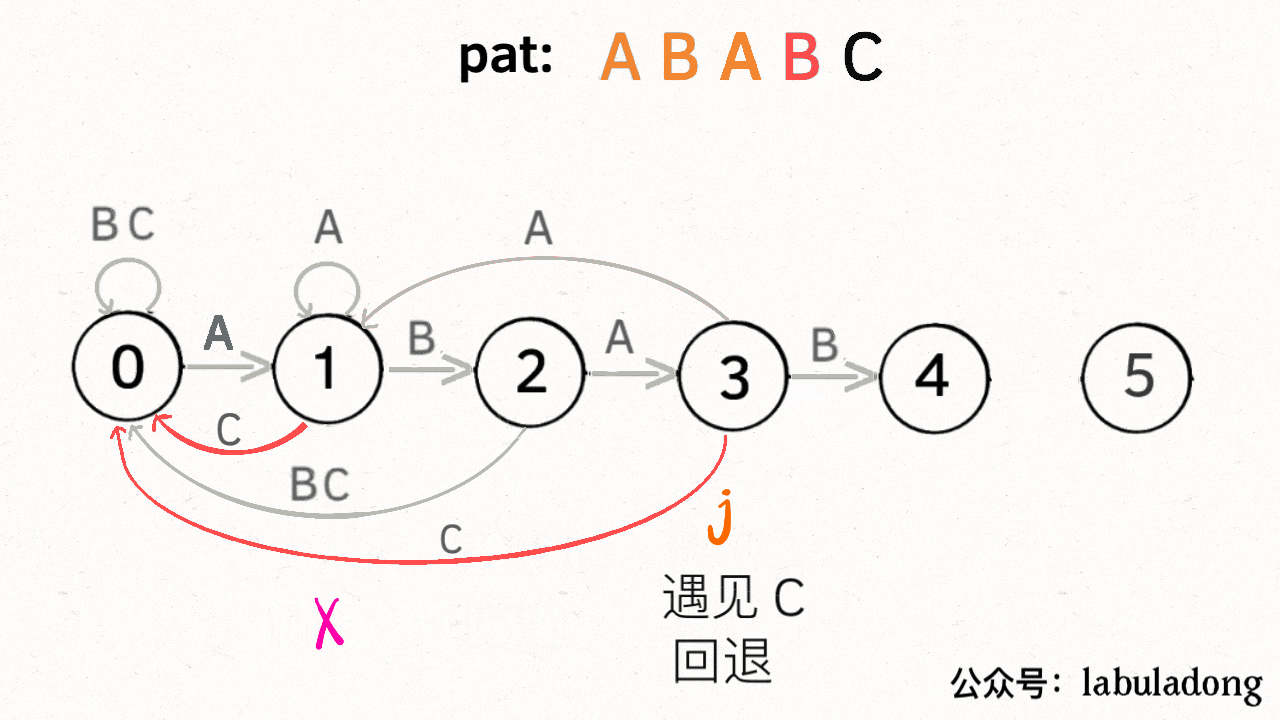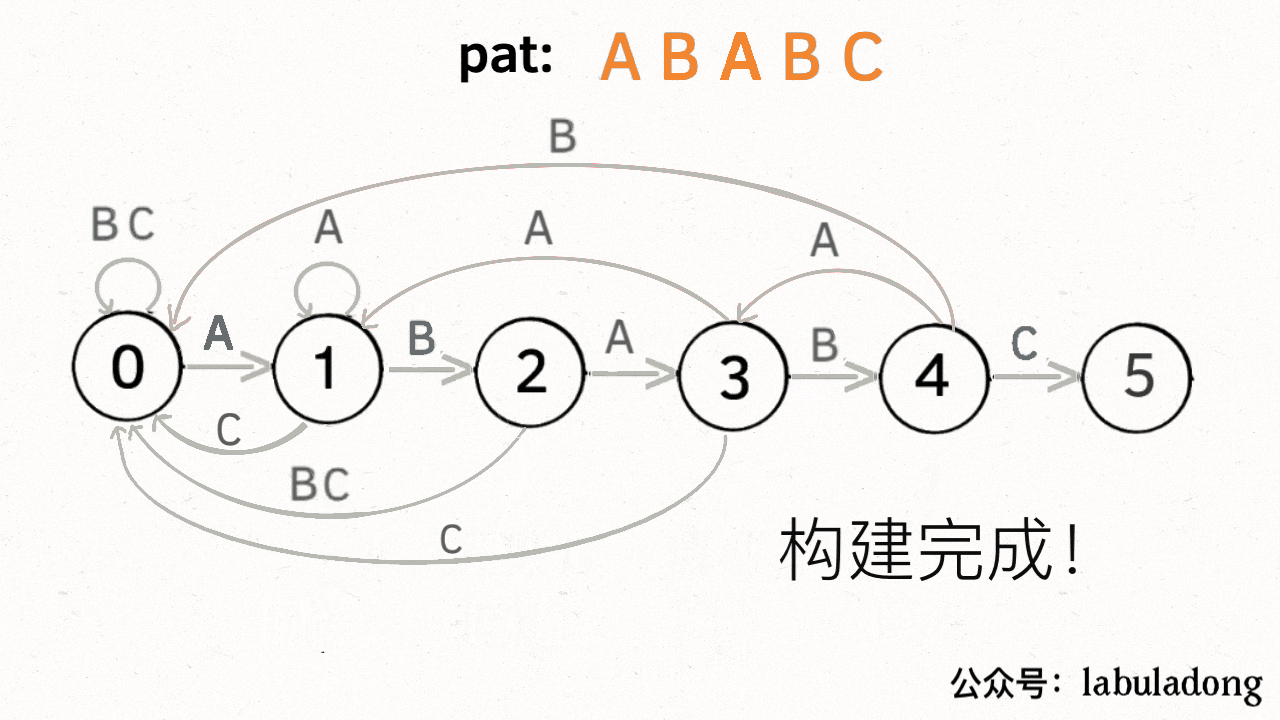
X = dp[X][慢指针的下一个 c]
X最多前进一步,它是看当前遍历到的,和慢指针是否一样,一样就一起往前走,只不过往前走用dp里的数字代替了
dp[快指针][下一个元素] += 1
dp[快指针][其他元素元素] = dp[x][快指针下一个元素] 一般是0 因为不匹配了
实现 strStr() (KMP)
在一个串中查找是否出现过另一个串
示例 1: 输入: haystack = “hello”, needle = “ll” 输出: 2
示例 2: 输入: haystack = “aaaaa”, needle = “bba” 输出: -1
KMP暴力匹配
// 暴力匹配(伪码)
int search(String pat, String txt) {
int M = pat.length;
int N = txt.length;
for (int i = 0; i <= N - M; i++) { //从头开始对每个字符都进行匹配
int j;
for (j = 0; j < M; j++) { //在里面开始对每个字符进行匹配
if (pat[j] != txt[i+j])
break;
}
// pat 全都匹配了
if (j == M) return i;
}
// txt 中不存在 pat 子串
return -1;
}



























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










