Backtracking algorithm梳理

回溯法简介
注意下面这句话
由于回溯通常结果集都记录在回溯树的路径上，因此如果不进行撤销操作， 则可能在回溯后状态不正确导致结果有差异， 因此需要在递归到底部往上冒泡的时候进行撤销状态。
如果你每次递归的过程都拷贝了一份数据，那么就不需要撤销加粗样式状态，相对地空间复杂度会有所增加

回溯法都可以抽象为树形结构，其实每一层都代表了一个for循环
以下面题为例，k=2时是两个for循环，k=50是50个for循环，后者写不出来，但是回溯能够写得出来。

77. 组合

给定两个整数 n 和 k，返回 1 … n 中所有可能的 k 个数的组合。
输入: n = 4, k = 2
输出:
[[2,4],[3,4],[2,3],[1,2],[1,3],[1,4]]

剪枝优化

class Solution {
public:
    vector<vector<int>> combine(int n, int k) {
        
        
        vector< int > temp;
        dfs(temp, n, 1, k);
        return ret;

    }
    void dfs(vector<int>& v, int n, int nowIndex, int k)
    {
        if (v.size() == k)
        {
            ret.emplace_back(v);
            return;
        }
        else if (nowIndex > n)
        {
            return;
        }
        //加入路径，遍历，消除关系
        for (int i = nowIndex; i <= n&& n-i+1 >= (k-v.size()); i++)
        {
            v.emplace_back(nowIndex);
            dfs(v, n, ++nowIndex, k);
            v.pop_back();        
        }
    }
public:
    vector<vector<int>>ret;
};

216. 组合总和 III

找出所有相加之和为 n 的 k 个数的组合，且满足下列条件：

只使用数字1到9
每个数字 最多使用一次
返回 所有可能的有效组合的列表 。该列表不能包含相同的组合两次，组合可以以任何顺序返回。

每个for循环也是从开始索引遍历剩下的数

class Solution {
public:
    vector<vector<int>> combinationSum3(int k, int n) {
        vector<int>temp;
        dfs(n,k,1,temp);
        return ret;
    }

    void dfs(int target,int k,int startindex,vector<int>&temp)
    {
        //找到目标值为target的 k个数
      //终止条件 1、当前为k个值了，并且目标值为0 即成功加入最后集合中
      //2、非正常结束 超过k个值了或者目标值小于0了，错误退出，直接return
      if(temp.size() == k && target == 0)
      {
          ret.emplace_back(temp);
          return;
      }
      //这里的等于是上面没有被挑选的
      else if(temp.size() >= k || target <= 0) return ;

      //正常逻辑，加入，执行dfs，取消加入 
      for(int i = startindex; i <= 9 || 10-i > k-temp.size() ; i++)
      {
          temp.emplace_back(i);
          dfs(target-i,k,i+1,temp);
          temp.pop_back();
      }
    }
public:
   vector<vector<int>> ret;
};

17. 电话号码的字母组合

给定一个仅包含数字 2-9 的字符串，返回所有它能表示的字母组合。答案可以按 任意顺序 返回。

给出数字到字母的映射如下（与电话按键相同）。注意 1 不对应任何字母。

输入：digits = “23”
输出：[“ad”,“ae”,“af”,“bd”,“be”,“bf”,“cd”,“ce”,“cf”]

如果用for循环怎么做
对于给的每个数进行循环
这里训练的是string的一些使用方法

39.组合总和

给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target ，找出 candidates 中可以使数字和为目标数 target 的 所有 不同组合 ，并以列表形式返回。你可以按 任意顺序 返回这些组合。

candidates 中的 同一个 数字可以 无限制重复被选取 。如果至少一个数字的被选数量不同，则两种组合是不同的。

对于给定的输入，保证和为 target 的不同组合数少于 150 个。

但还有种方法，要么加本元素，要么开始下一个元素（用这种方法）

class Solution {
public:
    vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
        vector<int>temp;
        dfs(candidates, target, 0, temp);
        return ret;
    }
    void dfs(vector<int>& candidates, int target, int startIndex, vector<int>&temp)
    {
        
        //1、返回，target = 0
        if (target == 0)
        {
            ret.emplace_back(temp);
            return;
        }
        else if (startIndex > candidates.size() - 1 || target < 0) return;

        //1、继续用当前值
        temp.emplace_back(candidates[startIndex]);
        dfs(candidates, target-candidates[startIndex], startIndex, temp);
        temp.pop_back();

        //2、用下一个值
        dfs(candidates, target, startIndex + 1, temp);

    }
public:
    vector<vector<int>> ret;
};

40. 组合总和 II

给定一个候选人编号的集合 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。

candidates 中的每个数字在每个组合中只能使用 一次 。

注意：解集不能包含重复的组合。

加上如下重复的判断，会出错，因为是从左向右判断的（有的编译器可能是相反的），因此需要将i>0放大前面。

 if (candidates[i] == candidates[i - 1] && i > 0)
    continue;

放到前面来

if (i > 0 &&candidates[i] == candidates[i - 1])
   continue;

但这样会出错，有的时候可能是重复的两个都加上，比如 1 1 5，这样加上判断后会省略当前的元素

如果加上used标记是否已经使用

或者不用used，直接用同一层的移动

二、切割问题

切割问题，切了以后两边就没有关系了
针对切割问题，可以通过for来的，就像下面图一样，第一层for循环，我可以选择在g切，也可以在goog处切，切了以后就没关系了，下次的递归是选择新的字符串的切割位置，也就是我切了以后，前边和后边就没有关系了，将前面加到容器里，这是产品。然后一直遍历，等到没地方切了，也就是切得位置到了最终位置，那么就是递归完成了，没有产品再往容器里放了

131. 分割回文串

给你一个字符串 s，请你将 s 分割成一些子串，使每个子串都是 回文串 。返回 s 所有可能的分割方案。
回文串 是正着读和反着读都一样的字符串。
google的[[“g”,“o”,“o”,“g”,“l”,“e”],[“g”,“oo”,“g”,“l”,“e”],[“goog”,“l”,“e”]]

class Solution {
public:
    vector<vector<string>> partition(string s) {
        //对于n判断后面的
        vector<string> cur;
        dfs(s, cur, 0);
        return ret;

    }
    //1、需要有个s，线回文串缓存，startIndex
    void dfs(const string& s, vector<string>&cur,int startIndex)
    {
        if (startIndex > s.size()-1)
        {
            ret.emplace_back(cur);
            return;
        }
        /*
        * 1、对于每一个加入startindex,判断加上这个是否是回文，是回文则开辟分支，让其进行下一个for循环
        * 2、不是则绕过
        */
        for (int i = startIndex; i < s.size(); i++)//在这层for循环里寻找一切可以切割的位置，然后切下去调用新的切割 
        {
            if (isHW(s, startIndex, i))
            {
                cur.emplace_back(s.substr(startIndex,i - startIndex + 1));
                dfs(s, cur, i+1);
                cur.pop_back();
            }

        }

    }
     bool isHW(const string &s,int Startindex,int Endindex)
    {
         while (Startindex != Endindex && Startindex < Endindex)
         {
             if (s[Startindex] != s[Endindex])
             {
                 return false;
             }
             else 
             {
                 Startindex++;
                 Endindex--;
             } 
         }
         return true;
    }
public:
    vector<vector<string>> ret;

};

93. 复原 IP 地址

终止条件为段数大于4，

三、子集问题

78. 子集

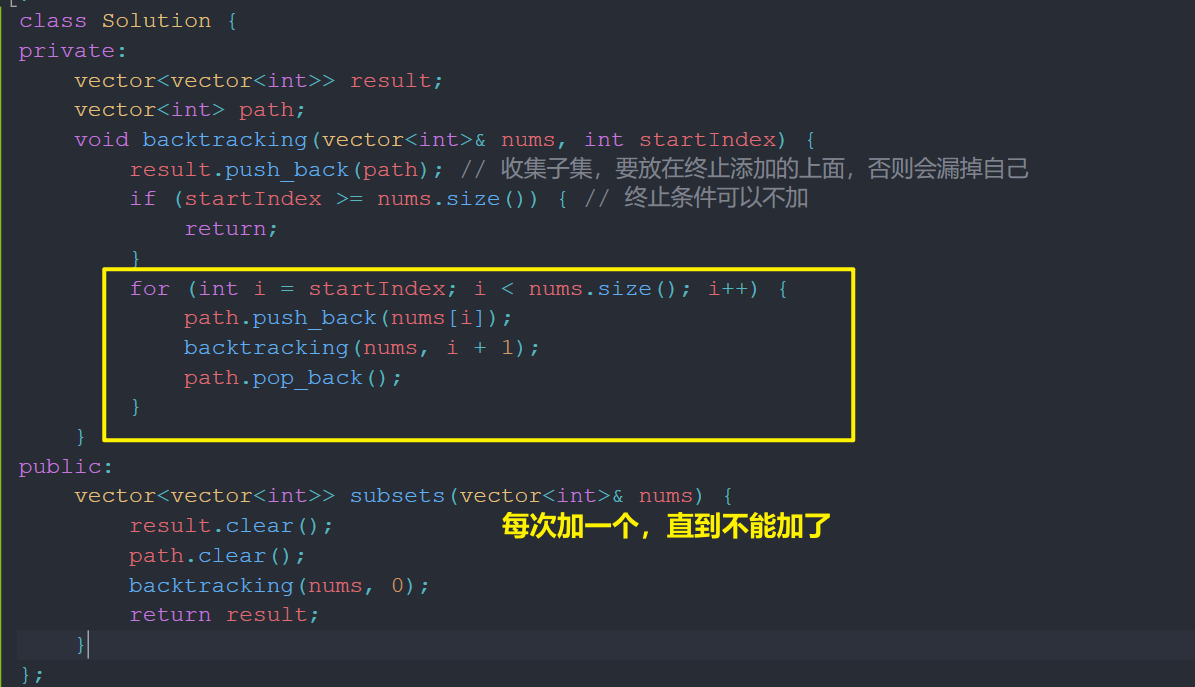
90. 子集 II

给你一个整数数组 nums ，其中可能包含重复元素，请你返回该数组所有可能的子集（幂集）。

解集 不能 包含重复的子集。返回的解集中，子集可以按 任意顺序 排列。

和上题一样，只不过要去除重复，本层不能有相同的，不同层的可以

491. 递增子序列

给你一个整数数组 nums ，找出并返回所有该数组中不同的递增子序列，递增子序列中 至少有两个元素 。你可以按 任意顺序 返回答案。

数组中可能含有重复元素，如出现两个整数相等，也可以视作递增序列的一种特殊情况。

在每执行一次dfs时都加入ret里面

46.全排列

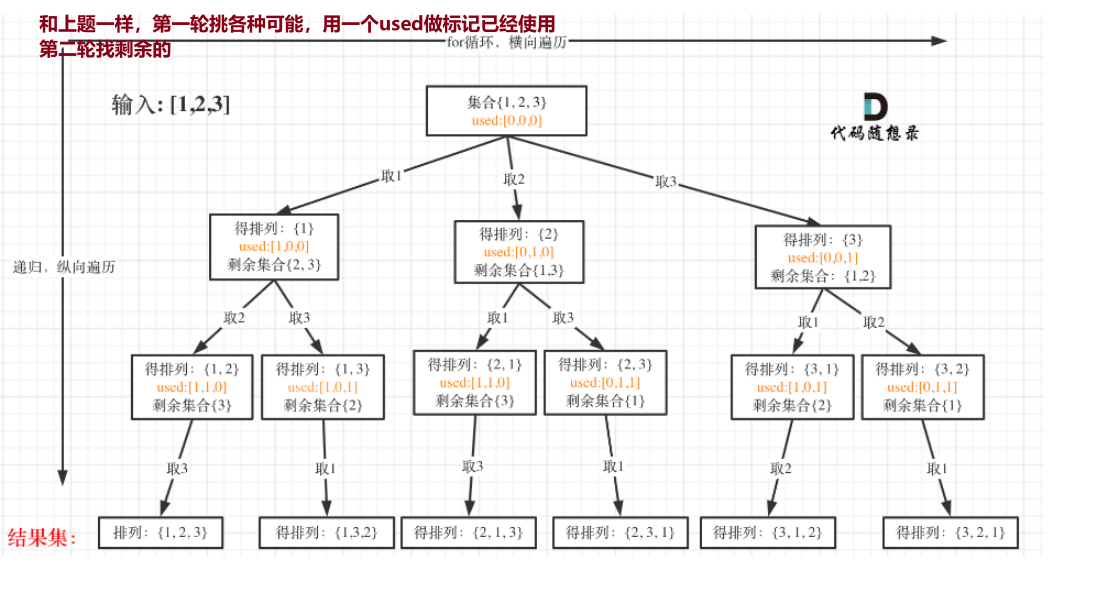
虽然这样看上去是层次一样的，但是用used的话，是每个分支弄完才会到另一个分支上，这个dfs是深度遍历的

47.全排列 II

同一层回溯，前面用了，后面就不能用