第三章 P3.1树和二叉树

1.树的一些概念

非空的树有根，树有子树，树和子树就像递归一样，树中有子树，子树这棵树又有子树，又有子树又有子树又有子树又.....如下图

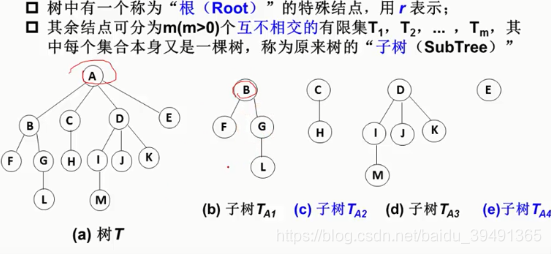
注意子树和子树不会有相交的结点

树是保证结点连通的一种最小连接方式，你随意去掉一条边，树就不连通了。

   

2.树的表示

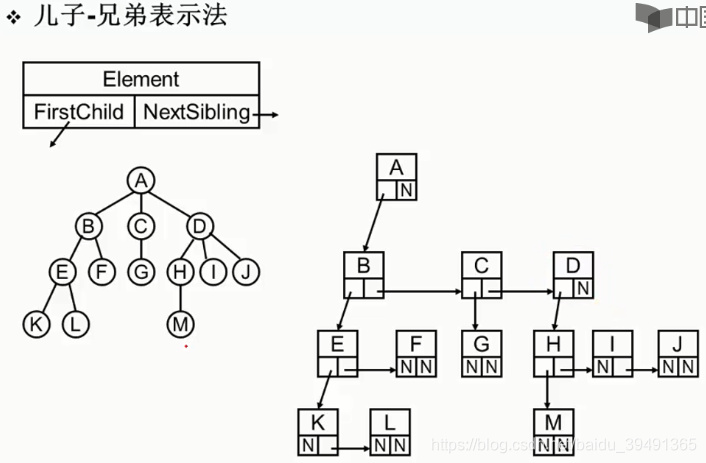
3.二叉树

把儿子-兄弟表示法的图旋转45度，可以看出，实际上是一个二叉树。

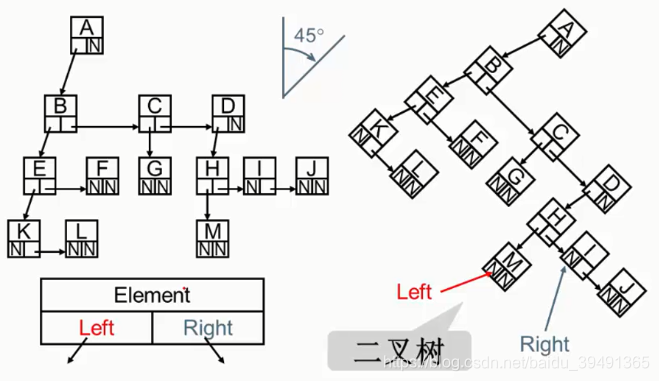
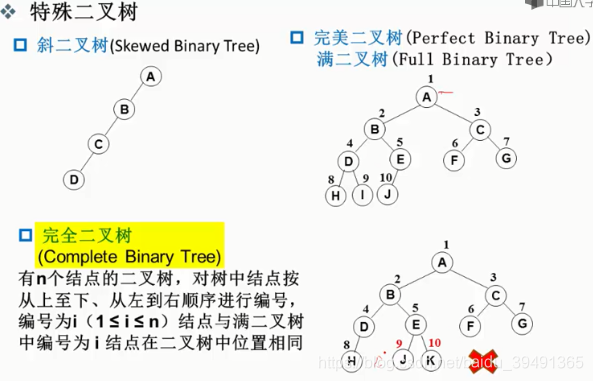
对于上图第三点，因为度表示子树的个数，所以也可以理解为，叶节点的个数是度为2的结点的个数+1。

证明：从边的角度来看 n0+n1+n2-1 = 0*n0+1*n1+2*n2化简得 n0=n2+1。

关于先序和后序可以这么记，都是先左后右，先、中、后指的是根是第几个看的。

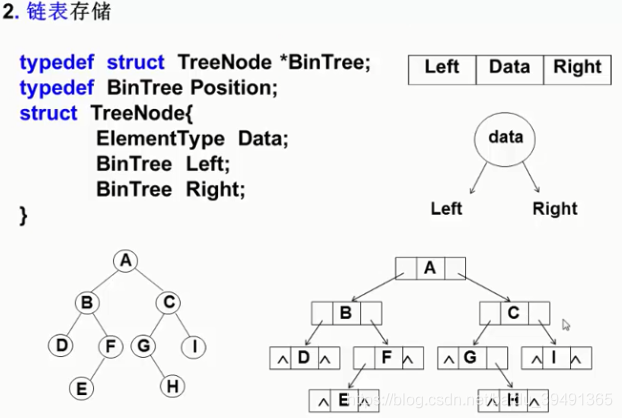
二叉树的存储结构

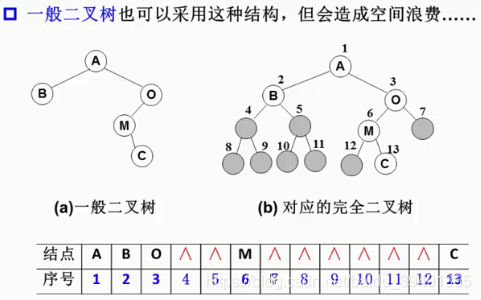
如果是完全二叉树，那么存储很简单，只需要用顺序存储就行了，具体就可以用数组。因为完全二叉树的根节点和左结点和右结点之间有关系。关系如下：

非根结点的父结点的序号是 i/2(取整没有左右结点之分了);

结点的左孩子序号是 2i;

结点的右孩子序号是 2i+1;

一般二叉树也可以用类似的方法，但是会浪费空间，因为要在空的地方进行补齐。

待续。。。。