汉诺塔问题与KMP算法

但行好事，莫问前程。

一、汉诺塔

话说在古埃及有一个三座塔，有一座塔从小到大，从上到下有64个金片，有一个和尚每天都在挪金片，将一座塔挪到另一座塔上，规定每一次移动都是大金片在上，小金片在下。还有一个传说，将这个金片挪完之时，就是世界毁灭之日。（故事可能略有出入，不过不重要，好吧）
如图，有3座塔

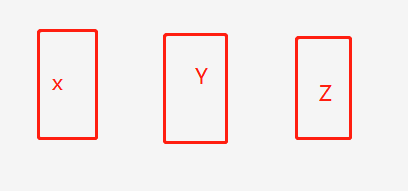
目的，将X上面的64个金片移动到Z上,简化为3步
1.将x上面63个移动到Y
2.将x上第64个移动到Z
3.将Y上63个移动到Z
分析第一步与第三步，将其拆分，可以分为62个金片的移动，由此，我们将问题规模极大的简化了，当最后只有一个金片的时候，直接移动就完事儿了。（ps: 金片==盘子 ）
代码如下

public static void move(int n,String x,String y,String z){

        if (n == 1){
            // 只有一个的情况
            System.out.println(count+"次移动>>>>第"+n+"号盘子从" +x+"移动到"+z);
            count++;
        }else {
            // 将 x剩下的63个通过z移动到y上
            move(n-1,x,z,y);
            System.out.println(count+"次移动>>>>第"+n+"号盘子从" +x+"移动到"+z);
            count++;
            // 将 y的63个通过x移动到z上
            move(n-1,y,x,z);
        }
    }

主函数如下

public static Long count = 1L;
    public static void main(String[] args) {
        move(3,"X","Y","Z");
    }

这里以3个盘为例

本来还想将64个盘子运行出来，等了很久，我还是太天真了。后来查了下资料，总次数为2^64-1,如果一秒移动一次，大概需要5800亿年。宇宙大爆炸至今才45亿年。这。。。。

KMP算法

KMP算法是一种字符串匹配算法，它的复杂度决定与模式串T而不是待匹配串S，这种算法就是为了避免无效匹配。下面举几个例子，
next数组的计算方法为，如果前面没有相同的元素，就为1，如果有一对，为2，如果有2对，为3，以此类推

S	9	a	c	a	b	a	b	a	a	c
T	4	a	b	a	c
next	X	1	1	1	2

S	9	a	b	c	a	b	c	d	a	c
T	4	a	b	c	d
next	X	1	1	1	1

S	9	a	a	a	a	a	c	a	a	c
T	4	a	a	a	c	b
next	X	1	1	2	3	1

第三个a时，第一个a与第二个a相同，第4个a时，a1 = a3,a12 =a23,有2对，所以为三，它的计算方法如下，
指定2个指针，一个指向模式串的前缀j，一个指向后缀i，以例三为例，c的前缀为a1,后缀为a3,如果前缀与后缀相等直接返回i+1的值，如果不等，j=next[j]的值，继续匹配,直到匹配上或者j==1时为止，
代码如下

public static char[] getNext(char[] chars) {
        char[] next = new char[chars.length];
        next[1] = 0;
        int i = 1, j = 0;

        while (i < Integer.parseInt(String.valueOf(chars[0]))) {
            // 前缀与后缀相等，next数组值为前缀的索引
            if (j == 0 || chars[i] == chars[j]) {
                i++;
                j++;
                next[i] = (char) j;
            } else {
                // 前缀与后缀相等，next数组值回溯到上一次j的next数组值
                j = next[j];
            }
        }
        return next;
    }

KMP算法最重要的就是求解到next数组，通过next数组拿到不匹配时应该用模式串哪个字符进行匹配。
定义两个指针索引，一个指向待匹配字符串s，一个指向模式串t，

1. 从索引值1开始进行匹配，匹配成功，两个指针往后移
2. 匹配不成功，如果t的索引值为1时，s继续往后累加，否者 s索引不变，t指向next数组t的索引值，再进行匹配
3. 直到s索引走到底，匹配成功，输出匹配信息，再继续往下匹配（规则：s串后一位与T串最后一位的next数组的下一位比对。继续往下匹配的操作不确定是不是对，测试好像是没有问题，当然，也可能是巧合，希望能够和大家交流交流）。
   代码如下

/**
     * 规定数组第一个个元素存数组字符串的长度
     *
     * @param s    目标串
     * @param t    模式串
     * @param next next数组---当字符串失配时，应该从模式串哪个位置进行匹配
     */
    public static void KMP(char[] s, char[] t, char[] next) {
        int sIndex = 1; // 目标串s的索引
        int tIndex = 1; // 模式串t的索引
        int tLength = Integer.parseInt(String.valueOf(t[0]));

        while (sIndex <= Integer.parseInt(String.valueOf(s[0]))) {
            /**
             * 字符匹配成功
             */
            if (s[sIndex] == t[tIndex]) {
                /***
                 * 模式串长度到达最后
                 */
                if (tIndex == tLength) {
                    System.out.println("匹配成功,s串索引值" + (sIndex - tLength + 1));
                    /**
                     * 下面这2步是我大胆假设的结果，不确定对不对，经过测试，好像没有问题
                     * 如果已经匹配了，s串后一位与T串最后一位的next数组的下一位比对
                     */
                    sIndex++;
                    tIndex = next[tIndex] + 1;
                } else {
                    /**
                     * 未到最后，进行下一位比对
                     */
                    sIndex++;
                    tIndex++;
                }
            } else {
                /**
                 * 前面第一位都不匹配，直接匹配s串下一位
                 */
                if (tIndex <= 1) {
                    sIndex++;
                } else {
                    /**
                     * 通过next数组决定下一位匹配哪个位置
                     */
                    tIndex = next[tIndex];
                }
            }
        }

    }

经过几次验证，都没有问题。
说明：为了说明算法以及好比对，通过数组的方式验证的算法，主要也是学习其中的思想，里面涉及到的bug以及算法的长度限制等bug或者不足我就主动性忽略了。其中有些表述可能还不是特别清楚，我会加油的。
奋斗路上，你我不孤单！！！
最后附上git地址: https://gitee.com/zhoujie1/data-structure-and-algorithm.git