古代游戏里的千年智慧

最新推荐文章于 2025-11-24 20:03:37 发布

原创最新推荐文章于 2025-11-24 20:03:37 发布 · 1k 阅读

22 ·

CC 4.0 BY-SA版权

文章标签：

#游戏 #游戏的历史 #游戏设计 #解谜游戏

游戏的设计专栏收录该内容

14 篇文章

订阅专栏

游戏自古有之：智力解谜、竞技体育、棋牌策略、童趣民间和宴饮社交游戏等，丰富多彩。

智力类游戏如九连环、七巧板、华容道都很有特色，其中九连环需要341步才能解开，七巧板能拼出超过1600种图案，这些游戏的设计都非常值得现代游戏设计是借鉴。古人的游戏充满智慧，兼具娱乐与益智。下面这个表格汇总了古代一些有代表性的游戏及其主要特点，方便快速了解：

游戏类别	代表游戏	主要特点与描述
智力解谜	九连环	用九个圆环相连成串，以解开为胜，解法复杂，最少需341步。
	七巧板	由七块几何板组成，可拼出超过1600种图案（人物、花卉、鸟虫等）。
	华容道	基于三国故事的滑块游戏，需要巧妙移动方块助“曹操”脱出，最少需81步。
竞技体育	蹴鞠	古代足球，战国流行，汉代用于军训，宋代有职业球会“齐云社”。
	马球（击鞠）	骑在马上用杖击球，唐代尤为兴盛，章怀太子墓有《马球图》壁画。
	投壶	由射礼演变而来，站在一定距离外将箭矢投入壶中，重在礼仪与专注。
棋牌策略	围棋	古老战略棋戏，春秋战国已流行，唐代设“棋待诏”官职。
	象棋	战国“六博”为雏形，宋代定型为现代象棋，有《橘中秘》《梅花谱》等经典棋谱。
	叶子戏	唐代出现的纸牌游戏，明代有40张牌，分文钱、索子、万贯三等，被视为麻将雏形。
童趣民间	放风筝	春秋发明，初为木鸢，汉代造纸术后普及，宋代成为民间娱乐。
	抽陀螺	新石器时代有陶制陀螺，宋代称“千千”，清代出现鸣声陀螺（空竹）。
	跳百索（跳绳）	汉代称“跳丸”，唐代发展为“透索”，宋代《武林旧事》载为元宵节游戏。
	斗草	分“文斗”（比花草名贵）和“武斗”（比草茎韧性），《红楼梦》中有描写。
宴饮社交	流觞曲水	酒杯放流水上，停谁处谁饮，王羲之《兰亭集序》记载的雅事。
	手势令（拇战、猜拳）	唐代已盛行，方式多样，如“童童猜”（类似石头剪刀布）、“内拳令”等。
	酒令（猜枚、射覆等）	宴席游戏，猜枚藏物于拳让人猜，射覆则用诗句典故隐喻，猜不中者罚酒。

本章重点介绍智力解谜类型游戏：

一、九连环

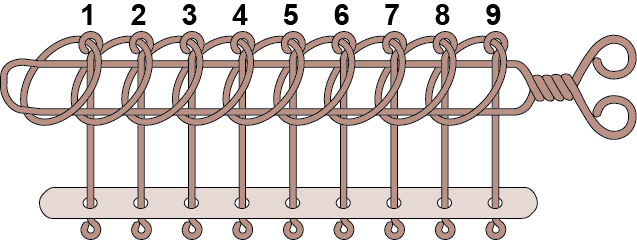
九连环不仅仅是一个玩具，它更是一个实体化的数学难题、一个机械思维的杰作、一个充满哲学隐喻的智慧结晶。

1.核心设计思维：递归与系统论

九连环的设计思维远超其时代，与现代计算机科学和系统论的核心思想不谋而合。其精髓可以概括为以下几点：

递归思维（Recursive Thinking）
- 这是九连环最核心的设计思想。要解开第 N 个环，必须先解开第 N-1 个环；而要解开第 N-1 个环，又必须先解开第 N-2 个环……如此递推，直到第一个环。反之，安装的过程也是递归的。
- 这就像计算机编程中的递归函数，一个函数在执行过程中会调用自身。九连环将这种“自相似”、“分而治之”的抽象思维过程，完美地物化成了一个可触摸、可操作的物理实体。玩家在操作时，实际上是在不自觉地训练和运用递归逻辑。
二进制与状态机（Binary & State Machine）
- 九连环的每个环都有两种明确的状态：“在柄上”或“不在柄上”。这完美对应了现代计算机科学的基石——二进制（0和1）。
- 整个九连环的解环过程，可以看作是在遍历一个有限状态机（Finite-State Machine）的所有状态。每一步操作（上或下）都使系统从一个确定的状态转移到另一个确定的状态。解开九连环所需的最少步数 (2^(n+1) - 2)/3（对于9环是341步）本身就蕴含着深刻的二进制数学原理。
拓扑结构与约束（Topology & Constraint）
- 设计者没有使用任何弹簧、磁铁或复杂的锁扣，仅仅利用一根金属杆和九个带有特定弧度的环，就创造出了一个极其复杂的约束系统。
- 环与环之间、环与杆之间的空间交错关系（拓扑结构）构成了天然的物理约束。一个环的状态会直接决定其相邻环能否被操作。这种设计迫使玩家必须遵循特定的、唯一的顺序，而不能靠蛮力或侥幸成功。它模拟了一个环环相扣、相互制约的复杂系统。
极简主义与优雅（Minimalism & Elegance）
- 九连环的构造极其简单，仅由若干金属环和一根杆构成，没有任何多余部件。但正是这种极简，催生了极大的复杂性。这体现了“少即是多”的设计哲学：用最简单的元素，构建出最丰富、最深奥的系统。

2.古人是如何构思出这种游戏的？

虽然已无确切史料记载其发明过程，但我们可以基于其设计进行合理的推测：

源于生活与实践的观察：
- 古人可能从套在一起的绳结、锁链、或是马车/帐篷的某种活动部件中获得了灵感。他们观察到了物体之间这种“相互嵌套、相互制约”的关系，并思考如何将其抽象化和游戏化。
对“难解之结”的痴迷：
- 中外文化中都有对复杂绳结的情结，如希腊的“戈耳狄俄斯之结”（Gordian Knot）。创造出一种看似简单、实则极难解开的“结”或“锁”，本身就是一种智力挑战和乐趣。九连环是这种痴迷的一个极致产物。
数学探索的实体化：
- 中国古代的数学成就斐然，尤其在算术和代数领域。虽然当时没有“递归”或“二进制”的现代理论，但数学家或智者可能已经在思考类似的序列和级数问题。九连环可以看作是这种抽象数学思考的一个实物模型或演示工具。通过操作它，可以直观地感受到一种严谨的、不可违背的数学规律。
哲学思想的隐喻：
- 道家思想：九连环的“环环相扣”可以隐喻世间万物的普遍联系和相互制约（“阴阳相生相克”）。而解开它的过程，则象征着破除执念、顺应规律（道）才能达到最终解脱的修行过程。蛮力无法解决，唯有理解并遵循其内在法则才能成功，这极具道家“无为而无不为”的智慧。
- 兵家思想：也可以看作是一场战争模拟。每个环像一个城池或一支部队，你不能直接攻击最终目标，必须循序渐进、步步为营，先扫清外围，削弱其与友军的联系，最后才能攻克主城。这体现了“步步为营”的战略思维。

3.总结：九连环的设计智慧

设计思维层面	具体体现	现代对应
数学思维	递归序列、二进制状态、最少步数规律	计算机科学、离散数学
机械思维	利用简单的拓扑结构创造复杂约束	机构学、自动化控制
系统思维	理解局部与整体的关系，操作具有严格的顺序性	系统论、项目管理
哲学思维	万物相连、顺应规律、以智取胜而非以力破巧	道家思想、策略思维

二、七巧板

七巧板的设计思维确实非常精妙，它将抽象的数学原理和美学融合在了简单的七块板中。下面这张图梳理了其核心的设计思维体系：

1.设计思维的核心维度

七巧板的设计思维远超其时代，其构思精巧体现在多个维度：

“以简驭繁”的模块化与标准化思维
- 设计者仅用七块标准几何板（5个等腰直角三角形、1个正方形、1个平行四边形），通过旋转、平移、翻转（特别是平行四边形的利用）这些有限的操作，就能组合出成千上万的图形。这体现了用最少的基本单元，通过组合创造最大多样性的模块化设计思想。
- 所有板块都源自一个标准正方形，各板块的边长之间存在严格的数学比例关系，确保了它们在任何组合中都能完美契合，无一多余或缺失。这种标准化是其能广泛流传的基础。
深刻的数学原理嵌入
- 出入相补原理：这是七巧板的核心数学基础，即一个几何图形被分割成若干部分后，这些部分的面积之和等于原图形面积。无论怎么拼，七块板的总面积恒定。
- 勾股定理与比例关系：七巧板的切割方式蕴含了勾股定理。各板块的边长均遵循特定比例，例如，小三角形的直角边记为1，则斜边为√2；中三角形的直角边为√2，斜边为2等。这种内在的数学规律是其严丝合缝的保证。
- 拓扑变换：平行四边形的引入是关键。它不同于其他三角形和正方形，允许通过翻转来改变朝向，这大大增加了拼图的可能性和灵活性，是解决许多问题的关键。
开放与创造性的游戏机制
- 象形与抽象：七巧板鼓励玩家从抽象的几何形状中识别和创造出具体的事物（人物、动物、建筑等），这是一种启发式思维训练，重在联想、概括和抽象表达能力。
- 规则极简，答案不唯一：游戏规则非常简单——“用七块板拼出某个形状”。但每个问题通常有多种解法，激发了玩家的探索和创造欲望，没有唯一的答案，培养了发散思维。
用户体验与情感化设计
- 手感与材质：传统的七巧板多为木制，提供了温润的触感和适宜的重量感，操作体验极佳。
- 难度梯度与成就感：从拼回正方形，到模仿给定图形，再到自由创作，难度自然提升，让玩家能在不断挑战中获得成就感。
- 文化寓意：“七”在中国文化中常与“巧”相连（如七夕乞巧），七巧板也承载了启迪智慧、祈求灵巧的美好寓意。

2.构思起源：从实用器具到益智玩具

七巧板的构思并非一蹴而就，其演变历程体现了设计思维的演化：

原型启发：“燕几”与“蝶几”
- 七巧板的直接灵感来源于古代一种称为“燕几”（或称“宴几”）的家具。“燕几”是宋代黄伯思设计的一套由七张可自由组合的桌子，可根据宴会人数和需求拼合成不同形状（如三角形、方形、长方形），可谓模块化家具的先驱。
- 明代严激又在燕几基础上设计了“蝶几”，由13件不同的三角形和梯形几案组成，能拼出更丰富多样的图形，形态如蝶翅。这为七巧板提供了更多的形状组合灵感。
关键飞跃：从家具到平板
- 古人将“蝶几”的原理从三维的桌几简化到二维的薄板，并固定为七块，形成了七巧板的雏形——“七巧牌”。这一转变使其从实用器具变成了纯粹的思维游戏，更便携，更专注于平面几何的挑战。
定型与传播
- 清初时，七巧板的形制基本定型。1813年，《七巧板合璧》一书出版，收录了大量图样，标志着其作为一种成熟的益智玩具被广泛推广和接受。
- 它流传到西方后，被称为“Tangram”（唐图），引起了极大兴趣，西方人对其数学原理进行了深入研究。

3.总结：穿越时空的设计智慧

七巧板是功能、形式与数学的完美统一。它用极简的元素，构建了一个充满无限可能的创造系统。其设计思维深刻体现了模块化、标准化、数学严谨性与开放性创意的平衡。

它不仅是一个玩具，更是一个数学教具（阐释几何关系、面积守恒）、思维训练工具（提升空间想象、逻辑推理、发散思维）和文化载体。历经数百年，其设计魅力依旧不减，持续启迪着各个年龄段的玩家，这本身就是其设计思维成功的最好证明。

三、华容道

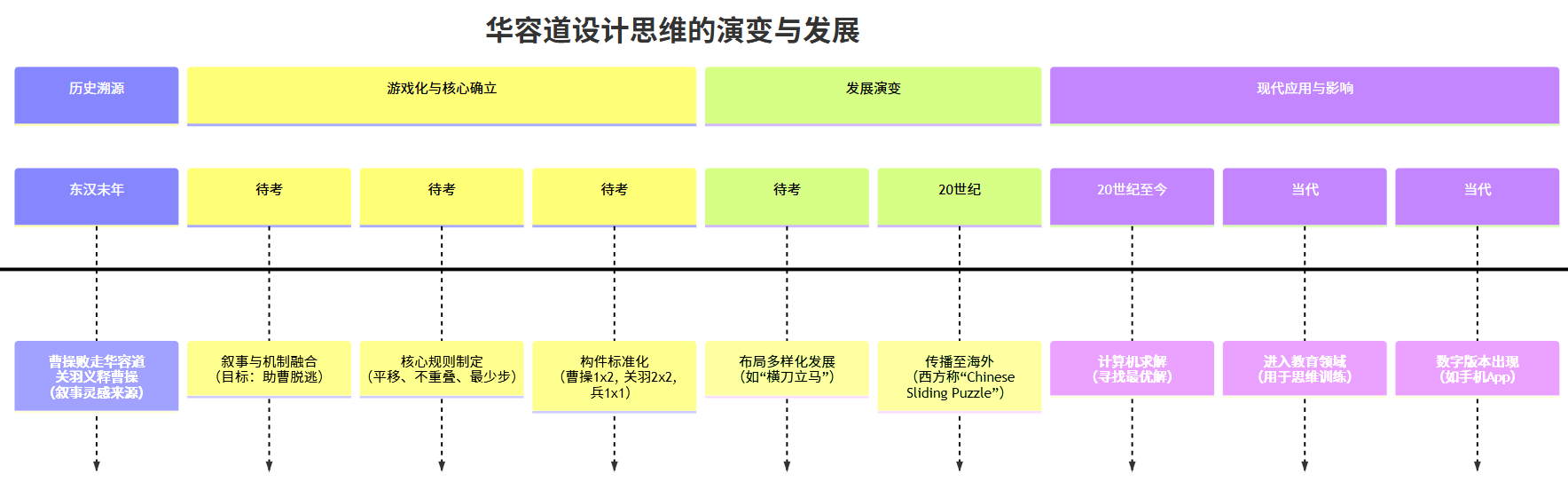
华容道是一款非常经典的中国古代益智游戏，它的设计思维相当精妙，融合了历史叙事、数学原理和空间推理。下面这张时间线梳理了华容道从历史渊源到现代应用的关键发展节点：

1.核心设计思维解析

华容道的设计思维远超其时代，其构思精巧体现在多个维度：

叙事与机制的深度融合：游戏灵感源自三国时期“曹操败走华容道，关羽义释曹操”的历史故事。设计者成功地将这一叙事内核转化为游戏机制：•
- 目标导向：游戏目标“帮助曹操从出口逃脱”直接对应故事结局。
- 角色赋予：不同大小的棋子被赋予了曹操、关羽、五虎将、小兵等具体角色，使其不再是抽象的几何块，而是承载了故事和关系的实体，增强了玩家的代入感和情感联系。
- 规则隐喻：棋子移动的“阻碍”与“疏通”，隐喻了故事中“围堵”与“放行”的矛盾，尤其是关羽（最大的障碍）同时也是放行的关键，完美对应了关羽在故事中“义释”的复杂角色。
空间与约束的精妙平衡：
- 有限空间：棋盘被设计为一个4x5的网格，仅留1到2个空白格作为移动空间。这种极强的限制性是所有挑战和策略产生的根源。
- 异构棋子：棋子并非单一尺寸，而是包含1x1（小兵）、1x2（五虎将横向）、2x1（五虎将纵向）、2x2（曹操）多种规格。这种异构性大大增加了移动的复杂性和策略深度，玩家必须考虑不同形状棋子的移动方式和相互制约关系。
- 简单而严格的规则：“所有棋子只能在平面内平移，不能拿起、跳过或重叠”。这条简单规则创造了巨大的思考空间，迫使玩家进行长链条的逻辑推理和精确的空间计算。
模块化与标准化的预设：
- 所有棋子都基于一个基本单元（小兵所占的1x1格子）进行设计。例如，曹操是2x2，横向武将是2x1。这种模数化设计确保了所有棋子都能严丝合缝地在网格中移动，不会产生无效或模糊的状态，体现了高度的严谨性。
开放与创造的无限可能：
- 多变的初始布局：通过改变少数几个大将的朝向（横置或竖置）和位置，就可以产生数十种甚至上百种经典的初始布局（如“横刀立马”、“近在咫尺”、“水泄不通”等），每种布局的解法路径和最优步数都不同。这赋予了游戏极高的可重玩性和探索空间。
- 从解谜到创造：高手不仅可以解题，还可以自己设计新的布局来挑战他人，实现了从“玩家”到“设计者”的思维跃迁。
最优解的追求与数学之美：
- 游戏鼓励玩家追求“最少步数”。这种对最优解的追求，使其超越了简单的解谜，上升到数学优化和算法思维的层面。例如，最经典的“横刀立马”布局，已知的最优解是81步。这种对精确和效率的追求，体现了深刻的数学之美和逻辑之美。

2.构思起源：从历史故事到智慧结晶

华容道的构思并非一蹴而就，其演变历程体现了设计思维的演化：

历史故事的启发：其直接灵感来源于《三国演义》中“诸葛亮智算华容，关云长义放曹操”的经典桥段。设计者巧妙地将文学叙事转化和抽象化为一个空间谜题。
滑块谜题的传承与发展：华容道属于“滑块类游戏”（Sliding Puzzle）。这类游戏古今中外都有，例如中国古代的“重排九宫”（八数码问题）。华容道的独特之处在于它引入了不同大小的滑块，并将它们与一个生动的故事相结合，使得其复杂度和趣味性远超许多同类游戏。
文化内涵的融入：“华容道”之名本身就充满了文化分量。它不仅是游戏，更是一种文化符号，承载了人们对历史、谋略、忠义和智慧的复杂情感和解读。