反射与折射

序

在这里看过：太极图形课S1第07讲：光线追踪实战_哔哩哔哩_bilibili

但是，当时只是看一下就忽略了。

最近要用了，才想起来。 回头重新看吧……

人教人,教不会,事教人,一次就好

大概是这个意思。

直观的认识

 先来点感性认识：

高中物理：光的全反射实验_哔哩哔哩_bilibili

反射与折射 

 

 全反射

入射角增加，折射角也增加；但是折射角先达到90度，也就是“消失”了。

折射率 

角度不同，反射光与折射光的强度也会改变

当入射角不断增加时

 当入射角角度超过临界值，发生全反射以后

 其它

类似的一些链接：

光-全反射_哔哩哔哩_bilibili

入射角超过临界值以后，就变成全反射了。 

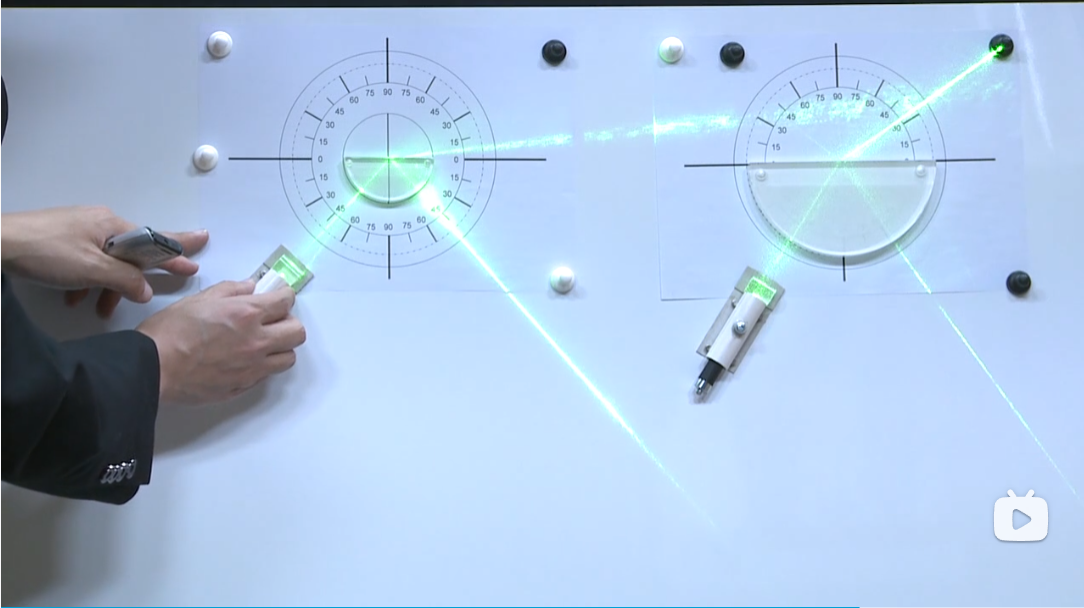
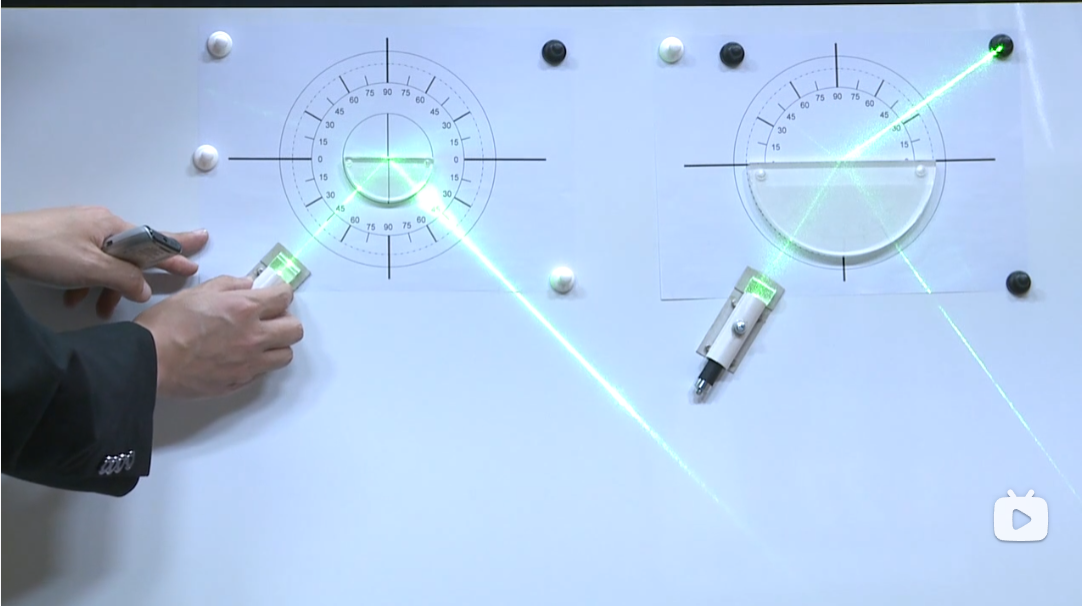 水槽里的全反射

 全反射_哔哩哔哩_bilibili

如果是垂直入射呢？

当光垂直射入水面时 发生折射吗？怎么折射？_百度知道 (baidu.com)

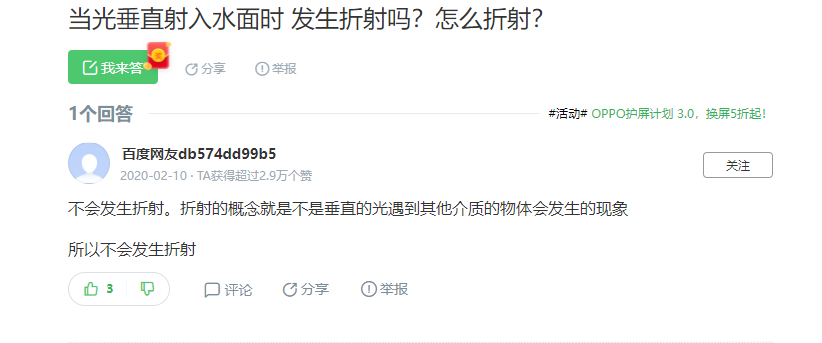 没毛病……

深入一些的认识

然后，再来点感性认识吧 

百度翻译

 

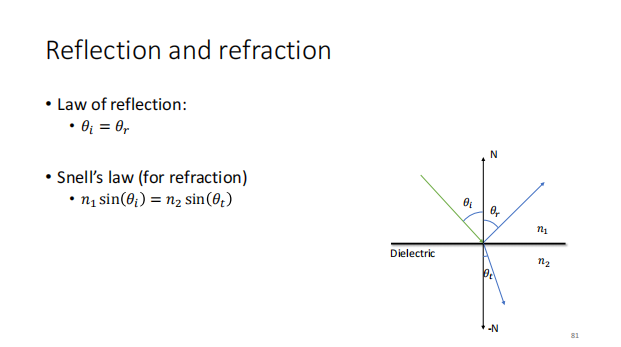
反射定律&折射定律

当光从一种透光材质射入另一种透光材质，会发生折射与反射

可以用折射定律和反射定律来描述这两种现象

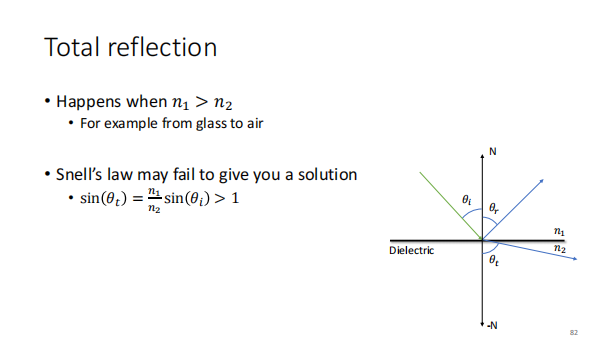
 全反射

当光从光密介质到光疏介质的时候，可能会发生全反射

好像是高中物理选修里的

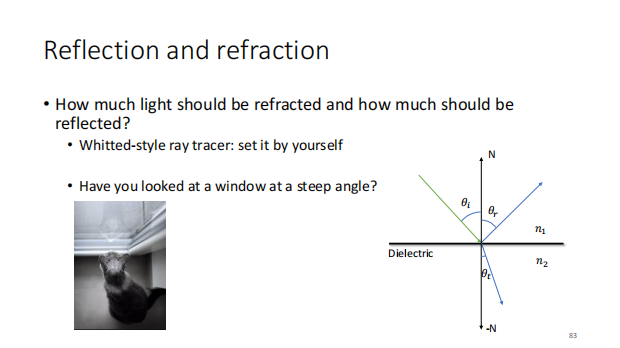
 反射与折射的比例

这个比例是啥？

Whitted里，这个比例靠自定义，很明显，这个不准。。 

怎么能准？

 有一个物理量——反射率，它描述的是有多少光被反射，和介质的折射率，光线的入射角有关。

R是反射，1-R说的就是折射

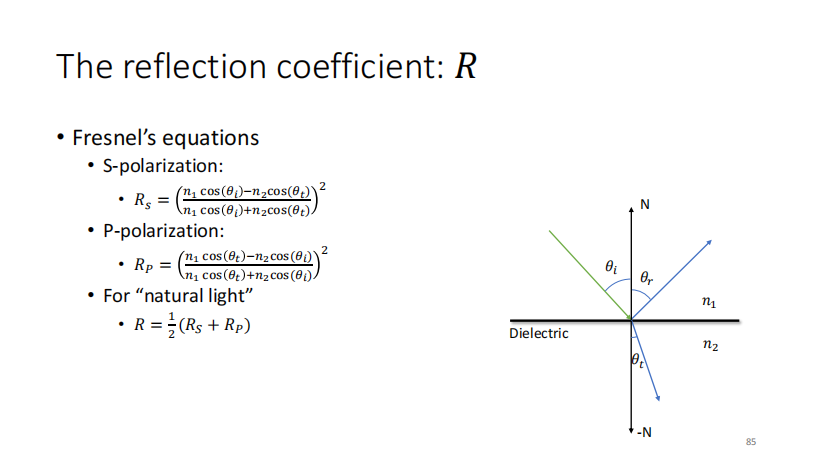
 然后这个R，可以这么算出来

RS：光的偏振方向和反射折射平面垂直时

RP：光的偏振方向和反射折射平面平行时

这和地震波的横波纵波有联系吗？

 这个R，也可以近似的算

西里克近似

•  和两材质折射率的差有关。当材质相同的时候，R0=0，全部投射，没有反射
• 和入射角有关。当入射角很小的时候，反射率R会很低，几乎全是透射；当入射角比较大的时候，反射的就变多了。【参考看远近的湖水。看近处，入射角小，透射多，能看到底。看远处，入射角大，反射率大，就看不到底，只能看到波光粼粼】

代码实现

先判断是不是全反射

不是全反射，就既有反射又有折射；具体到当前这条光线，就是折射一部分反射一部分。

在Whitted里，是这么实现的：入射一条，折射出去一条，反射出去一条，实现的时候需要手动定义一个栈，虽然麻烦，但是可以实现。

在PathTracing里，为了防止光线爆炸，PathTracing的框架是一次只发一条光线，递归到光源，结束【和入射一条出射两条这种情况不兼容】，然后多次采样计算平均。

怎么办？

计算和【两种光疏光密介质折射率，入射角度】这3个参数相关的反射率R。

丢个骰子，结合反射率R，来决定这次的光线到底是折射还是反射。 

这样多来几次，反射折射的比例也能模拟的差不多。

这部分引用自这个视频，19min左右：太极图形课S1第07讲：光线追踪实战_哔哩哔哩_bilibili

后记

这个里面也提了一下反射和折射：

GAMES101-现代计算机图形学入门-闫令琪_哔哩哔哩_bilibili