边缘中心高效回归分析

边缘中心高效回归分析

摘要

我们提出了一种边缘中心参数化预测分析方法，该方法有助于在网络边缘实现实时回归模型缓存和选择性转发，通过仅传播模型参数和充分统计量而非原始数据，显著降低了通信开销，同时实现了高分析质量。此外，我们引入了复杂的模型选择算法，用于结合多样化的本地模型进行预测建模，而无需在边缘网关处进行数据传输和处理。我们基于真实数据提供了数学建模、性能评估和比较评估，展示了该方法在边缘计算环境中的优势。

索引术语

在线回归分析，分析质量，通信效率，模型选择，向量量化。

一、引言

回归（预测）分析（RA）提供统计模型（例如，多元线性与分位数回归）以及数据中发现的模式，利用这些模型来预测新/未见数据，并研究未见数据如何适应这些模型[1]。实时RA[3],[4]在上下文数据从传感设备传输到云以在所有数据上构建全局在线模型后实现。然后，分析人员/应用程序对这些模型发出回归查询，用于实时数据探索、在线预测和自适应知识提取[5],[2]。然而，采用这种基线RA方法会带来重大挑战。需要大量原始数据传输以构建和更新此类模型。由于物联网环境受到有限网络带宽、计算能力、延迟和能源等限制，这变得不可行，因此边缘计算应运而生[10],[8],[6]。该范式可通过将尽可能多的智能计算逻辑推向靠近计算和传感边缘设备（EDs）的位置来应对这一挑战[1],[7]。因此，理想情况下，边缘设备应仅向云传输数据摘要，例如充分统计量和回归系数，以支持回归分析。

动机与目标

我们设想了一种以边缘为中心的实时分析范式，其中将边缘设备作为一流RA平台[15],[9]。我们的动机基于在边缘实现的实时分析，包括例如物理传感器（感知上下文信息）、用于参与式感知的移动边缘设备，以及与边缘设备和传感器/执行器交互的边缘网关（EGs），如图1所示。将实时数据从边缘设备传输到远程数据中心会带来网络延迟，这对交互式实时数据探索和推断分析应用是不利的；例如，城市监控应用会产生海量数据（测速摄像头；环境时间序列；地震监测），导致带宽受限完全实时迁移到云[9]。网络连接具有间歇性，如果云连接丢失，将导致功能丧失。云不应该是实时分析范式转变的万能解决方案。我们倡导以边缘为中心的实时分析，将分析前沿从中心节点推向网络外围。这种被推动的RA智能分布在边缘设备和边缘网关中。这引发了一种设想：边缘设备本地构建在线回归模型，并由边缘网关对其进行维护并选择性转发，以实现高效的模型选择和复杂聚合，而不是将原始数据从边缘设备发送到边缘网关和/或云。基于边缘设备与边缘网关之间仅模型通信的方式，我们希望在保持通信高效的同时，获得与基线RA集中式方法相当的RA质量/准确性。我们强调，我们的以边缘为中心的方法保留了使用云作为支持基础设施的核心优势，但鉴于边缘设备的计算能力仍在不断提升[9]，将实时分析处理重新放回边缘。我们的以边缘为中心的方法具备本地模型构建和高效模型更新的优势，能够及时响应输入信息，从而避免原始数据向中心位置集中，并保护敏感信息隐私。边缘网关则配备新颖的模型选择策略，以确定针对每个发出的回归查询最合适的本地模型。

挑战与期望

多维上下文数据具有诸如突发性和统计瞬变性等特殊特征，即值在短时间内过期，且属性之间的统计依赖性随时间变化[14],[4],[3]。因此，以边缘为中心的实时分析面临的挑战包括：（i）在边缘设备上进行在线本地模型学习，要求实时模型更新，并选择性地将模型转发到边缘网关，以最小化通信开销；（ii）最佳模型在边缘网关上根据每个回归查询进行选择；以及（iii）模型缓存技术，使其分析质量/准确性尽可能接近集中式方法。我们方法的期望特性为：（1）通过引入从边缘设备到边缘网关的选择性模型转发以及在边缘网关处的模型缓存，通信开销显著降低，因为仅传播模型参数和充分统计量，而非原始数据。这满足了所需的延迟和能效要求，并减少了闭环延迟，以实现实时上下文数据分析。（2）在边缘网关处的模型选择允许根据来自边缘设备的充分统计量，针对每个回归查询组合多样化本地模型，而无需在边缘网关上传输和处理数据。

II. 理论依据与问题基础

我们专注于参数回归分析，例如[2],[16],[14]在(d+1)维数据空间(x y) ∈ Rd+1中，我们试图学习输入x与输出 y之间的依赖关系，该输出由未知的全局数据函数 y= f(x) : x ∈ Rd估计。输入x=[x1, x2]可指代温度x1和CO2排放 x2等属性，而 y是湿度。一个回归查询表示为点q ∈ Rd ，使得我们在局部探索 f(x)在q附近的行为，并获得预测值ˆy= f(q)及其预测误差 e(q) = y − f(q)；例如，在给定q=[q1, q2]：温度 q1和CO2 q2的情况下预测湿度 y。

以边缘为中心的实时分析通过在边缘设备（ED）本地测量的输入‐输出对 {(x y)i} ∈ Rd+1，在线学习未知的回归模型 y= fi(x)。然而，由于每个边缘设备所处环境/上下文背景各不相同，例如智慧城市中的城市环境监测传感器在不同城区所经历的温度、CO2排放、紫外线辐射和湿度等数据范围存在差异或重叠，因此一个拟合所有数据并解释所有属性间统计依赖性的全局模型 fG 无法捕捉每个边缘设备中数据子空间的具体特征[14],。这就产生了为每个边缘设备建立局部模型 fi 的必要性，以表征其特定的本地数据 {(x y)i}，相关内容将在后文讨论。

我们应该高效且有效地将基于不同数据构建的多样化本地模型 fi 结合到边缘网关（EG）中，从而使EG能够解释多样的统计依赖性，并实时提供准确预测以响应查询。边缘设备（EDs）具备智能性的原理在于，它们选择性地将局部模型 fi 转发至EG，EG随后缓存这些模型，记作 fo i，以支持分析。显然，缓存模型替换是边缘设备智能的一部分，其在分析质量与通信开销之间进行权衡。

EG支持基于缓存的本地模型集合进行实时分析，通过对由边缘设备提供的缓存本地模型 F={f o 1,…, f o n} 引入复杂的模型选择机制。最终融合模型的表现应尽可能准确，就像事先已知 F 中哪个（些）局部模型最优一样。

特定查询以及在所有边缘设备收集的数据上表现最佳的全局模型 fG。显然，给定一个查询，在边缘网关上无法预先知道用于预测的最佳局部模型子集。此外，由于上述限制，我们无法在边缘网关或云上利用所有数据构建全局 fG ；为了效率，边缘设备不传输原始数据。

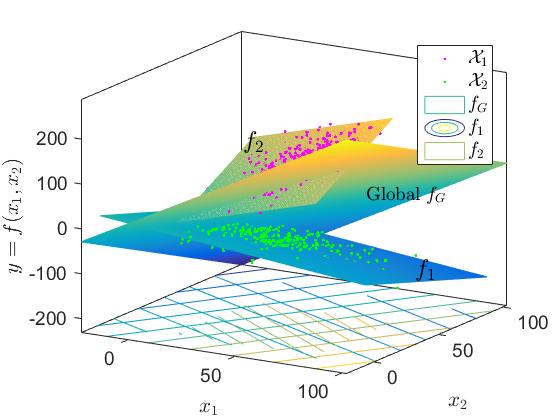
作为替代方案，模型选择可以简单地对所有本地模型进行平均：平均模型fAV G(x) = 1 n∑n i=1 fi(x)。然而，如图2、图3和定理1所示， fAV G会导致预测中不必要的较大变异性，从而降低准确率。具体而言，考虑在给定回归查询的情况下，局部模型 fi相对于全局模型和平均模型的预测误差差异 ΔeiG= eAV G − ei和 ΔeAV G i= eG − ei。

和本地‐全局模型多样性(δe G )的概率密度。)

然而，在现实中，此类信息并未提供，因此必须预测在边缘网关处针对任意回归查询应采用哪些最佳模型进行预测。如图所示，简单的模型平均方法在超过90%的情况下无法提供准确预测。原因是局部模型具有高度多样性，反映了边缘设备周围环境的特定特征。局部模型与平均模型的多样性 δe AV G = E[ 1 n∑n i=1(f i(x) − fAV G(x)) 2 ]被定义为来自局部模型和平均模型的预测结果的方差。图2（右）显示了 n= 25个模型的 δe AV G密度分布，表明局部模型之间的预测差异显著，并且与 fAV G 存在明显区别，因此，取平均会消除这些丰富的知识，导致预测不准确 （参见图3）。即使不考虑通信开销，将所有数据从边缘设备到云并集中构建/维护本地模型，因此，模型平均不是一个合理的解决方案。在我们的情况下，我们避免了用于本地模型构建/维护的数据传输，并要求在通信高效的同时获得尽可能高的分析质量，并重视本地建模的多样性。类似地，本地‐全局模型多样性δeG= E n1∑ n i=1(fi (x)−fG(x))2 表示全局 fG相较于fAV G能够提供更准确预测，但不如各个本地模型fi当我们知道q ∼ Xi(图2(左))。然而，这以显著增加通信开销为代价，涉及整个数据传输/模型维护，并且缺乏从本地建模中获得的知识。

EG智能的核心思想是，在无法在EG中对所有数据进行全局fG建模且不将任何数据从边缘设备传输到边缘网关的情况下，针对给定查询，通过适当的加权而非简单平均，选择性地调用部分缓存的本地模型。对于查询q，我们的挑战是预测在EG中最适合参与预测的本地模型子集 F′ ⊆F，使其精度尽可能接近fG，同时满足以下条件： (i) 通信约束，(ii) 缓存模型替换，以及(iii) 不了解输入数据{Xi} n i=1上查询的分布情况。

定理1.

设 eG、 eAV G和 ei分别为全球fG、平均 fAV G和本地 fi模型的预测误差。 eG< ei和 eAV G< ei并不总是成立。

证明。 为了证明定理1，假设其逆命题成立。那么只需给出反例即可。考虑多元线性回归 y ≈ f(x)= bx；其中b ∈ R d为系数。给定数据集 X= Xi ∪ Xj，其中Xi和Xj分别由边缘设备 i和边缘设备 j测量，我们在 X、 fi上构建全局 fG，在 Xi和 Xj上构建本地模型 fj，以及平均模型 fAV G= 1 2(fi+ fj)。对于查询q，如果我们得知q来自 Xi的数据分布，则应仅使用 fi，从而得到 ei< eG并避免对两个本地模型进行平均，此时使用 fi(q)会比使用 fG(q)和 fAV G(q)获得更优的预测结果，如图3所示（对于查询点 q1= 20，f2提供的预测值 f2(q1)比 f1、fG和 fAV G模型更精确，因为 q1 ∼ X2）。

A. 问题描述

我们的挑战是为每次查询预测最合适的F′ ，以实现几乎相同或希望比 fG和 fAV G更好的准确率，而无需将所有数据发送到边缘网关。

问题 1。 给定位于边缘设备 i 的局部模型 fi ，其图像 f o i 已缓存至边缘网关，定义一种在边缘设备 i 上的通信高效的模型选择性更新与交付机制，以替换边缘网关中的缓存模型，从而最大化分析质量。

问题 2. 给定在 EG 上一组缓存的本地模型 F={f o 1 ,…, f o n }，寻求一种模型选择方案以近似最佳 F′ ⊆ F，其准确性尽可能接近全球fG 已基于所有收集的数据构建，仅根据问题 1 中的更新机制分发本地模型。

问题3. 给定边缘设备 i 上的局部模型fi ，定义边缘设备 i 应向边缘网关提交的充分统计量，以指导问题 2 中的模型选择。

回归包括参数和非参数方法[16],[20],[17]。非参数方法使用存储的数据 X进行预测，在本场景中，这些方法在数据存储、计算以及对输入数据[17]的在线更新/ 适应方面计算效率较低。参数回归旨在从 X中寻找最优模型参数b，以最小化期望预测误差。参数模型具有以下优势：数据函数的可解释性更好，仅使用参数而非数据即可实现高预测效率，以及参数适应性[20]。本研究聚焦于参数回归分析。

Remark1. 我们的方法在参数回归模型方面是通用的。我们的算法仅从输入空间和预测误差中提取知识，而与边缘设备上的回归模型/参数的性质及其统计表达能力无关，具体采用哪种参数回归模型进行回归分析取决于应用场景/ 数据分析师决策。

B. 相关工作 & 贡献

相关工作： 在集中式方法中[14],[17]，所有收集到的数据都会被集中传输以进行分析，因此，集中式的回归建模与维护面临着大规模数据传输的沉重负担以及昂贵的融合中心成本。在某些情况下，网络节点可能由于隐私问题而不愿共享其原始数据。我们的方法将回归分析推向边缘，以应对上述限制。相比之下，参数回归的分布式方法 [16],[20],[3]明确关注于在节点上对全局模型参数进行分布式估计，其目标是实现与相应的集中式方法相同的预测性能，前提是将所有数据集中收集是昂贵甚至不可能的。分布式回归（i）未利用数据子空间局部性及本地模型多样性（而这些正是基于集成的RA中的关键组成部分，如上所述），（ii）专注于训练一个预定义的全局回归算法，其中所有参与的节点事先已达成一致，(iii) 在实时/自适应回归分析中需要额外的技术来进行参数更新与同步。这种方法强制要求节点采用相同的回归算法，而我们的方法则不需要，允许在边缘设备中灵活使用不同的回归模型；我们的方法依赖于本地模型的预测性能，而不受边缘设备所采用的回归算法影响。最近，提出了将分析推向边缘的方法，[12]要么简化为分布式参数回归[16]（其局限性如上所述），要么简化为选择性数据转发 [15],[11],[13]。具体而言，[15]处理在边缘设备和边缘网关之间的时间优化的数据转发，以最大化回归分析质量。该方法减少了网络边缘的数据通信，但数据处理和模型训练仍然集中在边缘网关上进行。这需要谨慎的数据传输来控制模型维护与自适应（见图1）。我们的工作进一步将模型构建、更新和维护推向网络外围（即边缘设备），从而完全避免了数据传输（同时也应对了数据隐私问题），仅将参数与充分统计量有条件地传播，用于模型适应与选择。文献[11]和[15]中的方法基于传感器上的本地预测模型进行数据抑制，旨在汇聚节点处重构数据。然而，它们并未关注在边缘设备（传感器）上进行回归/统计依赖性学习，而仅关注通过使用预测模型进行数据抑制来减少数据通信，这也已在[13]中讨论过。这些模型选择性地传播数据和单变量重构模型，供汇聚节点使用，因此实际的回归建模仍在边缘网关或汇聚节点完成，无法保证分析质量/预测性能。此外，回归建模不具备可扩展性，因为边缘网关缺乏模型选择和缓存机制来选择和维护最优的回归分析模型，除了简单的模型平均外，其局限性如上所述并在第五节中展示。

贡献： 据我们所知，这是首个以边缘为中心的在线参数回归分析方法，其贡献包括：（1）一种新颖的输入‐误差关联统计学习方法及其数学分析，用于提取可用于传输的在线充分统计量（问题3）；（2）一种通信高效方案，仅在边缘网络中传输模型参数与充分统计量，以实现边缘网关中的缓存模型更新（问题 1）；（3）在边缘网关上利用边缘设备提供的模型统计信息进行模型选择的新型算法（问题 2）；（4）基于真实数据对当前的全局与平均回归方法以及[15],[11]中的方法进行全面比较评估。

III. 边缘设备本地智能

本地决策

图1中的ED i基于滑动窗口Ni ={(x y)t − N+1,…,(x y)t} 内的近期本地数据，本地学习一个参数回归模型 fi( x)，例如 fi( x)=b i(x)，其中包含最近的N个观测到的输入‐输出对(x y)。记b i 为当前局部模型fi 的参数，b o i 为参数缓存的局部模型fo i，其中边缘设备 i在过去某个时间点已将其发送至边缘网关。边缘设备 i负责在局部 fi与边缘网关处的缓存 fo i之间预测性能出现显著差异时，更新边缘网关。边缘设备 i在本地保留一份 fo i副本以支持后文所述的决策过程，仅在必要时才发送参数bi。该决策必须通过实时顺序观察输入‐输出对来做出。考虑一个离散时间域t ∈ T={1, 2,…}。边缘设备 i在时间t捕获第 t个输入‐输出对(x y)t，并实时进行如下判断：情况A：判断该输入‐输出对(x y)t是否显著改变了当前局部fi的预测性能。在此情况下（情况A.I），边缘设备 i将(x y)t添加到窗口 Ni中，并丢弃最旧的一对，然后根据更新后的 Ni相应地调整或重新训练 fi 。否则（情况A.II），给定(x y)t，不对接收 fi进行调整或重新训练。情况B：判断在情况A.I中调整或重新训练后的局部fi是否应发送至边缘网关。在此情况下（情况B.I），若发现其与缓存 fo i相比存在显著的预测性能差异，则边缘设备 i使用最新的 fi更新边缘网关。否则（情况B.II），边缘设备 i与边缘网关之间不执行模型更新和传输。

在情况A中，边缘设备 i应能立即确定新数据对是否来自由 Ni中的数据对定义的输入‐输出子空间。在前一种情况下，新数据对在当前输入‐输出数据子空间内进行插值，因此被视为熟悉的。这种熟悉度表明，对于第 t个输入xt，当前模型 fi预计能够提供一个良好的预测值ˆyt= fi(xt)，即|yt − ˆyt| ≤ ε，其中 ε> 0为准确率阈值。在这种情况下，由于第 t个数据对是熟悉的（情况A.II），边缘设备 i无需调整或重新训练当前模型 fi，因此不需要与边缘网关进行通信。

如果第 t对被认为是相对于当前输入‐输出子空间不熟悉（novelty），则需要对当前模型 fi进行重新学习/自适应（情况A.I）。通常情况下，自适应/再训练后会得到一个新的局部模型 fi，从而使得边缘设备 i能够检查新模型 fi与缓存模型f o i之间的瞬时模型性能差异（情况B）。我们将此差异量化为第 t对输入下 fi和 f o i的预测误差的绝对差，即 |ei(x)t−eo i(xt)|。如果该差异超过差异阈值 θ> 0，则边缘设备 i应将新模型 fi更新至边缘网关，并在本地将缓存模型更新为 f o i = fi（情况B.I）。否则，即使缓存模型和新模型不是同一个，也无需边缘设备 i向边缘网关更新；这些模型的相似性由该差异表示，即若 fi和f o i 在 θ上的预测性能相同，则认为它们是相似的。因此，我们要求边缘设备和边缘网关均持有预测行为相同的模型。

备注2. 对于在新样本对 (x y) 上的参数自适应 b i ，可以采用(A1) 基于滑动窗口的批量重训练方法在窗口 Ni 上对 fi 进行重新训练，或 (A2) 例如使用在线/随机梯度下降（SGD） 来增量更新 b i 。例如，在线性回归中，在情况 A1 下，bi=(∑N l=1 xl xl)−1(∑ N l=1 xlyl)如果新奇性对(x y)相对于普通最小二乘优化被插入到 Ni中，而在A2情况中， bi通过SGD进行增量更新，即Δbi= −α(y − fi(x))x； α ∈(0,1)。该模型更新实践超出了本文的范围；读者可参考[19]以了解高效的参数回归自适应方法。

局部模型交付机制

挑战在于定义一种在线方法来评估新数据对的新颖性，因为基于此决策，边缘设备 i 可以触发向边缘网关的模型更新过程。新输入 (x y) 的新颖性可能同时触发局部模型自适应和缓存模型更新。其思想是增量式地学习第 k 个向量输入子空间，并同时将模型预测性能与该输入子空间相关联。为了实现这种关联，我们需要在线量化（划分）输入空间为 K 个未知子空间，每个子空间由一个输入原型 wk ∈ R d, k ∈[K] 表示，然后将位于原型 wk 附近的输入 x 上的预测误差 e(x) = y − fi(x) 与一个误差原型 uk ∈ R 相关联； k ∈[K] 是 k= 1, …, K 的紧凑表示法。也就是说，一个新的输入 x 首先被映射到最近的 wk，然后相应的误差 e(x) = y − fi(x)： k= arg mink∈K‖x − wk‖ 被误差原型 uk 所概括。这种关联的原理是，我们将 fi 在输入子空间（由 wk 表示）中的局部性能与局部预测误差（由 uk 表示）相关联。原型 uk 提供了关于 wk 周围子空间中模型准确率的局部知识，该知识将在后续用于指导边缘网关根据查询进行模型选择。

我们提出了一种新颖、快速且增量的输入‐误差空间量化方法，适用于未知原型数量的边缘设备 i K。在本方案中，目标联合优化函数最小化以下两项：(i) 输入空间中的条件期望量化误差 (EQE)，用于学习表示输入空间中新颖性的最佳输入原型；(ii) 条件期望预测误差(EPE)，用于学习捕捉局部模型性能的最佳误差原型。该条件基于最近输入原型，即我们优化输入/误差原型 Ci= Wi ∪ Ui，其中Wi={wk} 和 Ui={uk}，以最小化联合EQE/EPE：
$$ J({wk , uk}) = E[\lambda|x− wk|^2+(1 −\lambda)|e(x)− uk| \mid k] \quad (1) $$
其中Ak ≡{k= arg minl ∈[K]‖ x − wl‖ 2 }, e(x)= |y − fi( x)| 为绝对预测误差， λ ∈[0, 1]是用于权衡输入‐误差空间量化重要性的正则化因子； λ= 1表示已知的等效量子效率[18],，λ → 0表示纯基于预测误差的量化；期望值是对输入‐误差对(x e(x)) ∈ R d× R取的。

显然，原型 K的数量无法先验得知，边缘设备 i会根据输入的新颖性和模型性能逐步决定何时添加新的输入‐误差原型。因此，我们提出一种演化算法，该算法从初始的一个(K= 1)输入/误差原型对（w1, u 1 ）开始最小化(1)，该原型对对应于第一个输入x 1 以及给定的绝对预测误差 u 1 = |fi（x 1 ） − y1 |第一对（x1, y1）。然后，当前原型和新原型分别根据输入对的出现情况进行条件自适应和创建，体现熟悉度和新颖性的概念。具体而言，基于新输入x与其最近原型wk之间的熟悉度阈值 ρI，以及当前误差y−fi(x)的动态变化误差容限ρO，将对（x y）相对于迄今为止观察到的对分类为新颖或非新颖。如果相对于最近历史，该新对被视为熟悉，则最近输入原型及对应的误差原型将适应此熟悉对。然而，如果在最近输入子空间上的当前预测误差不可接受，即大于 ρO，则该容限 ρO会降低，表示对未来输入在误差空间中的容限减少。如果输入x相对于其最近的wk较远，且相对于 ρI，则创建一个新的输入‐误差原型。如果当前预测误差不可接受，即大于 ρO，则该对被视为新颖，这将立即触发模型重新学习/自适应。否则，由于当前误差可被接受，该对为熟悉，从而避免模型自适应/重训练。然而， ρO会降低，表示对未来新颖输入在误差空间中的容限减少。

演化算法1通过增量式地调整输入和误差原型来最小化(1)，如定理2所述。注意，wk和 uk会收敛到第 k个输入‐误差子空间中输入x的质心（均值向量）以及绝对预测误差的中位数，如定理3所述。这些（收敛后的）原型即为充分统计量 Ci（问题3），边缘网关EG将利用它们来针对发往EG的查询确定最合适的模型（图1）。

定理2 （自适应）

原型（wk, uk） ∈ Ci最小化(1)当且仅当给定一对（xt, yt） 时，它们被如下更新：
$$ \Delta wk= \alpha_t\lambda(xt − wk) \quad \Delta uk= \alpha_t(1 − \lambda)sgn(et − uk), \quad (2) $$
αt ∈(0,1)是学习率：∑ ∞ t=1 αt= ∞和∑ ∞ t=1 α2 t<∞, et= |yt − fi(xt)|，而sgn(·)是符号函数。

证明. 由于篇幅限制，证明省略。

定理3 （收敛）

原型（wk, uk） ∈ Ci分别收敛到第 k个输入-误差子空间的输入向量的质心和预测误差的中位数。

证明. 由于篇幅限制，证明省略。

算法1在ED上执行以下操作：(i) 通过最小化(1)对输入‐误差空间进行最优量化；(ii) 在线决定(x y)是否新颖，用于触发模型自适应和/或缓存模型更新；(iii) 通过识别 Ci 中的新原型实现增量演化。它返回更新后的统计信息Ci 以及对(x y)的分类结果，判断为熟悉或新颖性。当(x y)被判定为新颖时，EDi决定进行缓存模型更新。由于新颖性可能触发潜在的模型修改，ED i预期将获得一个新的局部模型，并评估该新模型与缓存模型之间的性能差异 |ei( x) −e o i( x)|，给定输入 (x y)。基于此性能差异，ED i决定是否将新模型发送至 EG以更新其缓存。ED i的局部决策过程如算法 2 所示；ED i 拥有其输入‐误差空间中所有可用的知识，这些知识已编码在 Ci 中。

算法1 边缘设备 i上的在线局部算法

输入： 新对 (x y)
输出: 熟悉度；更新的原型 Ci

1: 熟悉度 ← FALSE
2: 最近输入原型 k= arg min∈[K]‖x − w‖
3: 模型预测：ˆy= fi(x)；绝对误差 e= |y − ˆy|
4: 如果 (‖x −wk‖≤ ρI) 那么
5: 原型自适应: Δwk= αλ(x− wk)
6: 原型自适应: Δuk= α(1 − λ)sgn(e− uk)
7: 如果 e> ρO 那么
8: ρO=max( 12ρO, ρ∗ O)；适应模型 fi 关于 (x y)
9: else
10: 熟悉度 ← TRUE
11: 结束如果
12: 否则
13: 新颖性（新原型）： K= K+1，wk= x， eK= e
14: 如果 e ≤ ρO 那么
15: ρO= max( 1 2ρO, ρ∗ O)；熟悉度 ←TRUE
16: else
17: 适应模型 fi 关于 (x y)
18: 结束如果
19: 结束如果

算法 2 边缘设备 i上的本地决策

输入： 输入‐输出观测对 (x y)

1：从算法1获取对 (x y) 的熟悉度
2: 如果 (x y) 是新颖的（不熟悉）则
3: 在窗口 Ni 中追加 (x y)；适应/重新训练模型 fi
4: 模型预测误差： ei(x)= |y − fi(x)|
5: 缓存模型预测误差： eio(x)= |y − f o i(x)|
6: 如果 |ei(x) − eo i( x)| > θ 那么
7: 更新边缘网关以使用新模型 fi
8: 更新缓存模型 f o i ← fi
9: 结束如果
10: 结束如果

IV. 边缘网关智能

至此，我们已经详细阐述了如何为边缘设备 i学习输入‐ 误差空间，通过从局部模型 fi获取瞬时反馈，并生成充分 统计量（优化后的参数） Ci。这些统计信息被边缘网关接收， 作为指导依据，用于为每个查询选择最合适的模型。我们的 目标是实现实时分析，要求具备低通信开销且具有高准确率。其中，通信开销是指所有边缘设备 i向边缘网关传输 Ci 和 fi的开销，而高准确率则指在给定回归查询时具有较低的预测 误差。边缘网关缓存从各个边缘设备 i接收到的所有本地模 型 F={f o 1 ,…, f o n} 。根据算法 2，每个边缘设备 i独立自 主地决定是否将最新的局部模型 fi 更新至边缘网关，而无 需与其他边缘设备协同。部分更新的统计量 C i 会被发送至 边缘网关。

显著推动模型选择。注意：边缘设备仅在边缘网络内传播知识 （模型和充分统计量），而不传播用于实时分析任务的实际数 据。假设分析人员/应用程序向云发起查询流q ∈ Rd ， 该查询被定向到边缘网关EG；参见图1。EG应返回： （i）来自融合预测模型的精确预测值ˆy ，和/或（ii）在 由查询点q定义的输入空间周围当前本地模型的推断表示。这些结果必须高度准确，并在无需与边缘设备进一步通信 的情况下实时交付。因此，给定查询q，边缘网关EG面临 的挑战是：（i）高效地选择最合适的模型子集 F′ ⊆ F， 以提供集成预测ˆy，使其预测误差尽可能接近全局 fG； 以及（ii）提供F′中最具代表性的模型，以更好地解释输 入‐输出依赖关系。我们引入了模型选择方法，充分利用 来自边缘设备的所有知识。我们将集成预测ˆy建模为缓存 模型个体预测ˆyi= fo i(q)的加权和：
$$ \hat{y} = \sum_{i=1}^{n} f^o_i(q)\beta_i(q). \quad (3) $$

公式(3)中的权重 βi(q)是关于q的函数，用于解释局部模型 fi在由充分统计量 Ci导出的查询q附近的熟悉输入子空间 中性能的重要性。 βi(q)的取值决定了F′ ⊆ F的定义，其中 边缘网关仅利用 F′中的模型进行实时分析。我们提出以下 模型选择方法：

简单模型聚合 (SMA)

SMA 在集成结果中不利用从 边缘设备收到的统计信息 Ci。边缘网关仅聚合各个预测 值 ˆyi= f o i(q) 以得出最终预测，即设置 βi(q) = 1/n：
$$ \hat{y}=f_{AVG}(q) = \frac{1}{n}\sum_{i=1}^{n} \hat{y}_i. $$
边缘网关由边缘设备 i 在 缓存模型 fi更新时独立更新，而任何边缘设备均无需接 收Ci。集成子集 F′ ≡ F,，即无模型选择性，其预测准 确率相较于全球 fG未占优势；参见第五节评估结果。

输入空间感知的top‐K模型（IAM）

我们首先提出 top‐1（最优）模型选择方案（K= 1）。边缘网关仅选择一 个（最优）模型 f ∗ ∈F用于执行实时分析，即针对给定的查 询q（ F′={f ∗ }）。该模型选择通过使用在边缘网关接收到 的充分统计量 Ci的原型{wi,k}来实现。IAM选择这样一个 模型f ∗：其第个输入原型w ∗ 相对于所有模型的所有输入原 型W={{w1,k} k 1 k=1 ∪ ··· ∪{wn,k} k n 距离最近，即w∗ =arg min w ∈ W‖q −w‖。边缘网关选择其 输入子空间（由w∗ 表示）与查询点q最熟悉（最近）的模型， 因此，对应的预测模型 f ∗能够提供最佳预测结果。若未获取 每个模型的全部输入原型 Wi ，边缘网关则无法判断哪个模 型的输入子空间与给定查询点最为熟悉。IAM中的权重函数 表示q到所选原型w ∗ 的最短距离： β i(q) = 1 if∃wi,k ∈ Wi: wi,k = w∗ ；否则为0。边缘网关仅启用与最近原型相关联的 f ∗进行预测，即
$$ \hat{y} = f^ (q). $$
对于 K> 1，EG根据所有原型w ∈ W 与查询q的距离进行排序，并选择其最近输入原型位于前 K个最近距离中的模型f ∗ 1,…, fK ∗ ∈ F′ ⊂ F。集成预测 为：$$ \hat{y}=\sum_{i=1}^{K} f^ i(q)\beta^ _i(q)，$$ 其中 β ∗ i(q)相对于前K个逆距 离归一化为[0,1]。
$$ \beta^ _i(q)= \frac{e^{-|q-w^ {i,\ell}|^2}}{\sum {l=1}^{K} e^{-|q-w^ {l,\ell}|^2}}. \quad (4) $$
通过指数逆平方距离加权e−‖q−w‖2实现距离 ‖q−w‖的影响， 即越靠近q，权重重要性越高。

输入/误差空间感知的top‐K模型（IEAM）

EG利 用来自 Ci, ∀i的所有知识，结合模型关于查询q的输入子 空间熟悉度，通过最近输入原型wi,以及由误差原型反映 的相关性能ui,。IEAM从 F中选择最优或top‐K个最佳 模型，这些模型不仅在被查询输入方面具有熟悉度，而且 在其所熟悉的、由查询点的最近输入原型表示的子空间上 的局部预测性能方面也有效，能够提供准确预测。输入空 间熟悉度和相关预测性能这两个维度的结合，使得EG能 够进行更复杂的模型选择。权重 βi(q)表示考虑（逆向） 最近输入距离wi, ∈ Wi以及该子空间周围相关的绝对预 测误差中位数ui,后，模型相对于所发起查询的接近程度。 度量具体而言， βi(q)解释了模型 fi相对于查询q的相对 接近程度：
$$ \beta_i(q)= \frac{e^{-|q-w_{i,\ell}|^2} (1 - \bar{u} {i,\ell})}{\sum {l=1}^{K} e^{-|q-w_{l,\ell}|^2} (1 - \bar{u} {l,\ell})}, \quad (5) $$
其中$$ \bar{u} {i,k}= \frac{u_{i,k}}{\sum_{u \in U} u} $$ 是模型 fi在所有误差中位数 U={{u1,k} k 1 k=1 ∪··· ∪{un,k} k n k个输入/误 差子空间的预测误差的归一化中位数。预测结果通过从 F 中选择基于 βi(q)排序后 closeness 程度最高的前K个模 型 K ≥ 1得到，即$$ \hat{y}=\sum_{i=1}^{K} f_i(q)\beta_i(q)，$$ 其中 βi(q)由 公式(5)给出。

V. 性能与比较评估

实验设置与指标。我们在来自英特尔伯克利研究实验室的 ED/传感器的真实数据上，评估并比较SMA（fAV G ）、IAM和 IEAM与Global（fG ）（集中式方法）以及[11]和[15]中模型 的性能1。我们使用两个EG，每个EG连接 n= 25个ED；每个 ED每31秒采集一次温度、湿度和光照的三维向量（在36天内每 个参数包含230万数值）。每个ED i在大小为 N= 120个向量 的滑动窗口（1小时历史）上学习一个线性回归模型 y= fi( x)= b i x ，其中 d= 2维输入x=[x1 , x 2]（x 1 =湿度， x 2 =光照）， 输出 y=温度，并在算法1中进行适应并生成 统计信息 Ci。学习率 α= 0.1[17] 和正则化 λ= 0.5 在 （1）中用于平衡 EQE 和 EPE 的重要性。熟悉度阈值 ρI 在输入域 [0, 1]d 中进行归一化处理，即 ρI/√d ∈(0, 1)； 接近 1 的值表示粗向量量化，因此原型 K 较少，而接近 0 的值表示细粒度量化，因此原型 K 较多。在更新模型 参数时，每个边缘设备 i 中的差异阈值 θi= γMEDi， 其中因子 γ ∈(0, 3] 和 MEDi 是算法 2 中误差差异 |ei (x)−eio(x)| 的中位数，用于控制边缘设备与边缘网关之间 的预期通信。基于 θi，初始误差容差 ρO= θi 取最小值 ρ∗ O= θi 20。性能指标包括：(i) 所有模型相对于全局模型 的预期通信百分比：基线解决方案为将所有原始数据发送 至边缘网关以构建全局模型 fG；(ii) 每查询RA的预测准 确率，通过均方根误差 RMSE=[ M1 ∑ M m=1(ˆym − ym) 2]1/2 和平均绝对误差 MAE= 1 M ∑ M m=1 |ˆym − ym| 来衡 量。我们通过仅向边缘网关发送模型参数和统计信息而非 原始数据，评估与全局模型相比的通信节省情况，同时使 用 RMSE 和 MAE 来评估 SMA、IAM、IEAM 和 DBP [11], HOVF [15] 在相同回归查询 M= 3000 上的准 确性。HOVF 和 DBP 使用线性预测模型来预测边缘设备 的数据，每个属性独立建立一个模型，并将预测值与当前 值进行比较。如果差异小于容差值，则 DBP 保持空闲状 态，而 HOVF 决定是否仅向边缘网关发送数据；否则， DBP 为每个属性构建新的预测模型，并将新模型和数据 传输至边缘网关。在 HOVF 和 DBP 中， fi 回归模型在 边缘网关中构建。为了便于比较，DBP 和 HOVF 的窗口 大小和容差值分别设为 N= 120 和 θi。

性能与比较评估。我们评估了初始假设，即对于每个查 询q，无法知晓应选择哪个最佳本地模型 fi，因为我们无法 确定q是否属于 ∼ Xi，而全局模型的表现仅次于已知的最佳 本地模型，SMA的准确率最低（图2(左)）。图4(左)展示了 IAM、IEAM、SMA和全局模型相对于已知最佳本地模型 fi 的MAE差异：使用IEAM时，72%的情况能达到与全局模型 相同的准确率，IAM在52%的情况下达到相同准确率，而 SMA仅有16%的情况与全局模型准确率相当。这表明I EAM和IAM能够在无需将原始数据传输到边缘网关的情况下， 在边缘网关中为每个查询识别出最合适的本地模型，从而实 现通信高效并生成与全局模型一样准确的预测。图4(右)展示 了每个边缘设备上原型数量 K对应的熟悉度比率 ρ I /√d； 随着该比率趋近于1， K呈负指数下降，表明在不传输数据 的前提下，为达到与全局模型相同的预测准确率，边缘设备 上的最小存储需求得以保留。我们设定 ρ I /√d=(0.05,0.1)， 平均获得 K=(32,18)个原型每ED。我们进一步考察了通 过因子 γ调节的差异阈值 θ对减少 边缘设备与边缘网关之间的通信以及均方根误差（ RMSE）的关系。图5（左）展示了随着 γ的增加， IEAM（K= 1,ρI= 0.1）和IAM（K= 1,ρI= 0.1; K= 2,ρI= 0.05）相较于SMA在鲁棒性方面的表现，这 意味着模型更新的通信量更少，因此RMSE高于全球模型 （Global）。当γ< 1.5时，IAM和IEAM的RMSE显著低 于Global；而SMA在所有 γ情况下均表现出较高的 RMSE。为了更好地说明IAM和IEAM在RMSE与通信之 间权衡的效率，图5（右）显示IEAM的通信量显著减少 了80%，同时其RMSE仅略高于Global。注意：IAM和 IEAM中RMSE的增加与通信量的减少并无高度相关性， 因为在高通信情况下的误差几乎与几乎无通信时的误差相 同。这表明边缘网关（EG）基于统计信息 Ci识别出最 适合预测的模型，并且仅需来自边缘设备的少量通信更新。 通过SMA可以看出统计信息在寻找最佳模型方面的重要 性，而非简单地对模型进行平均——即使显著增加通信量， SMA也无法达到与其他模型相近或较低的RMSE。图6展 示了我们的模型与HOVF和DBP在准确率和通信方面的比 较。IEAM最为高效，利用边缘设备的统计信息 Ci以最少 的通信实现了高准确率；DBP和HOVF虽然通信高效，但 除了选择性数据传输外，并未考虑属性间的依赖关系，这 对RMSE产生了负面影响。最后，SMA相比Global在较 少通信的情况下实现了更高的准确率，但由于未考虑局部 模型的误差行为，因此准确率低于IEAM。

VI. 结论

一种新颖的、以边缘为中心的回归分析方法被提出，用于在线回归模型缓存和在网络边缘实现通信高效的分析。通过仅传播模型参数和 充分统计量而非原始数据来实现这一目标，同时该方法引 入了知识驱动的模型选择算法，从而获得高质量的分析效 果。在真实数据上与基线模型及文献中的模型进行性能和 比较评估，验证了其在边缘计算中的优势。