matlab:双或三方演化博弈，lotka-Volterra 1.双方演化博弈：代分析稳定点分析，代绘制相位图

matlab:双或三方演化博弈，lotka-Volterra 1.双方演化博弈：代分析稳定点分析，代绘制相位图，matlab仿真图代码
2.三方演化博弈：代分析稳定点分析，代绘制相位图，matlab仿真图代码3.lotka-Volterra模型

YID:7350644023709252

资料来源于 https://www.liruan.net/963.html

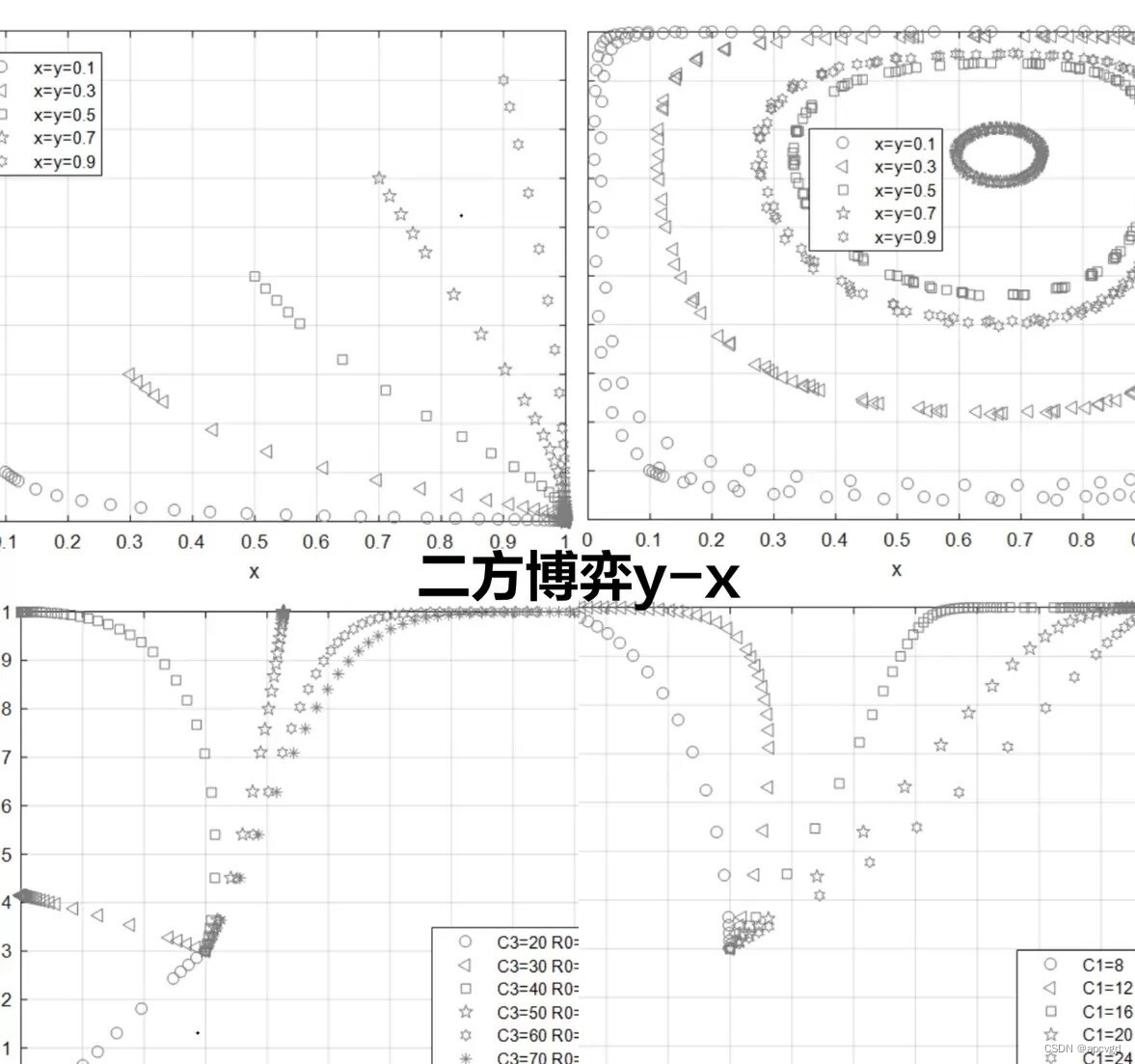
在现代社会中，演化博弈理论已经在许多领域得到了广泛应用，尤其是在计算机科学和人工智能领域。其中，双方演化博弈和三方演化博弈是非常重要的研究方向。本文将对这两种演化博弈进行深入分析，并介绍如何使用Matlab对其进行分析和仿真。

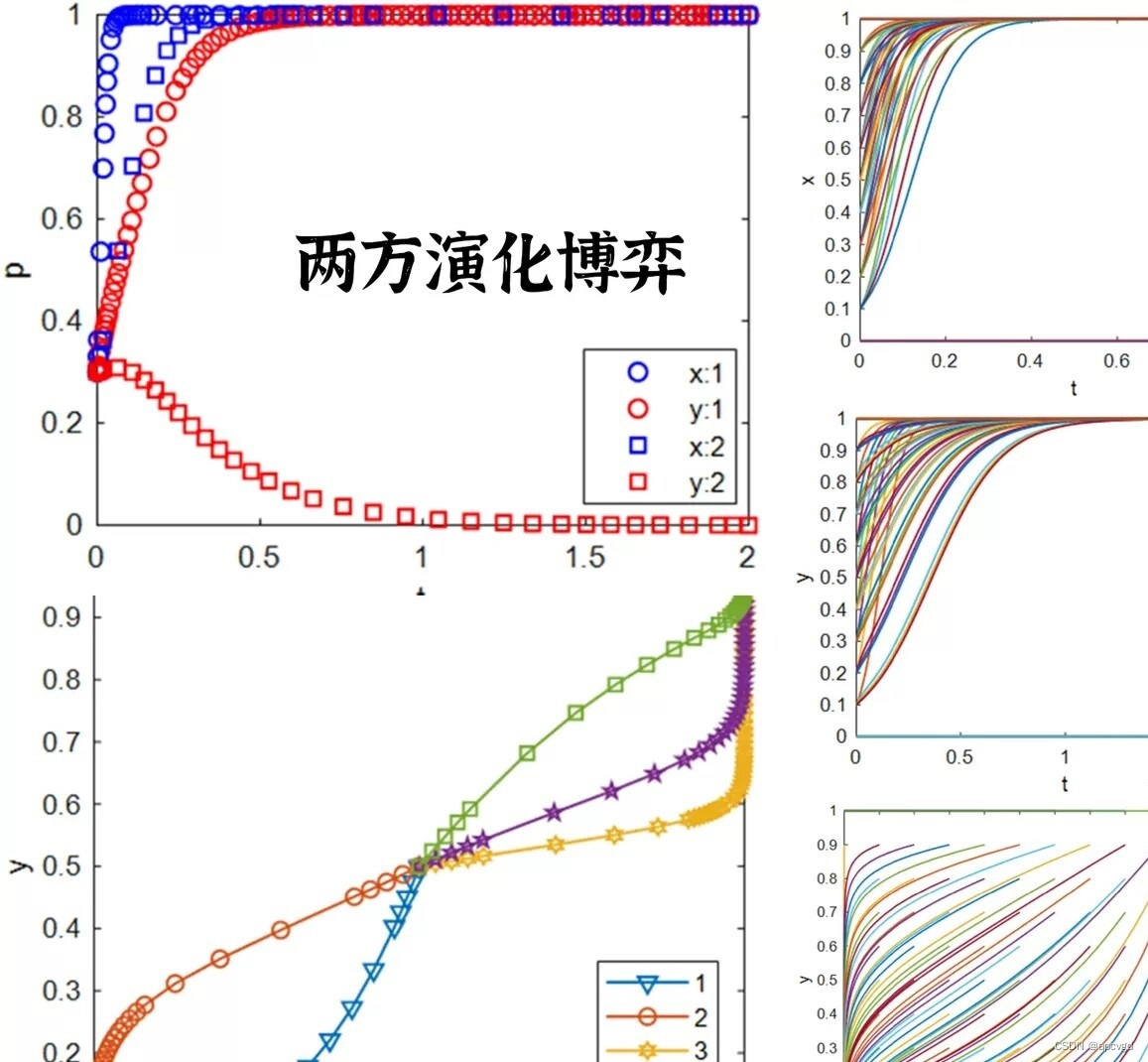
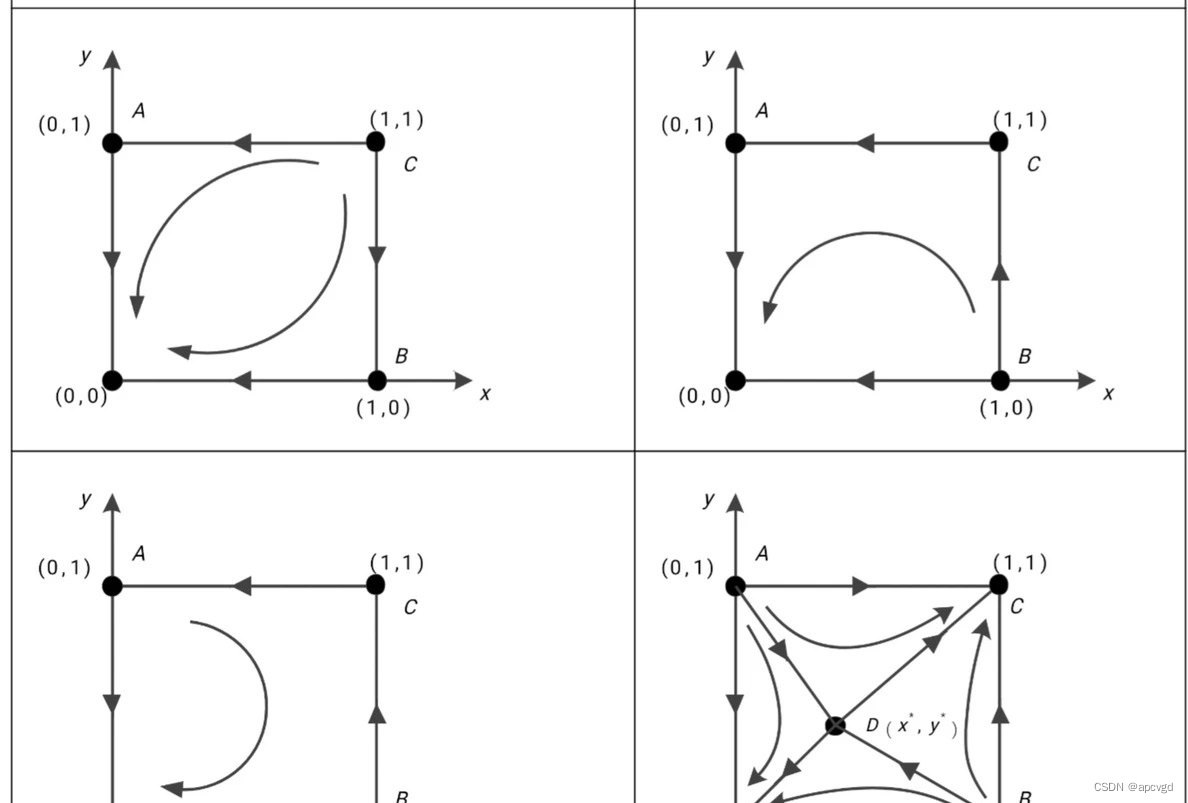
首先，让我们来看看双方演化博弈。这种博弈模型是指在两个对手之间进行的竞争过程。在这个过程中，每个对手会根据其策略来进行行动，从而达到一个最佳策略。在这个模型中，我们可以通过代数的方法来分析其稳定点，并通过绘制相位图的方式进行可视化。同时，我们也可以通过Matlab的仿真代码来模拟整个演化过程，并对其进行更详细的分析。

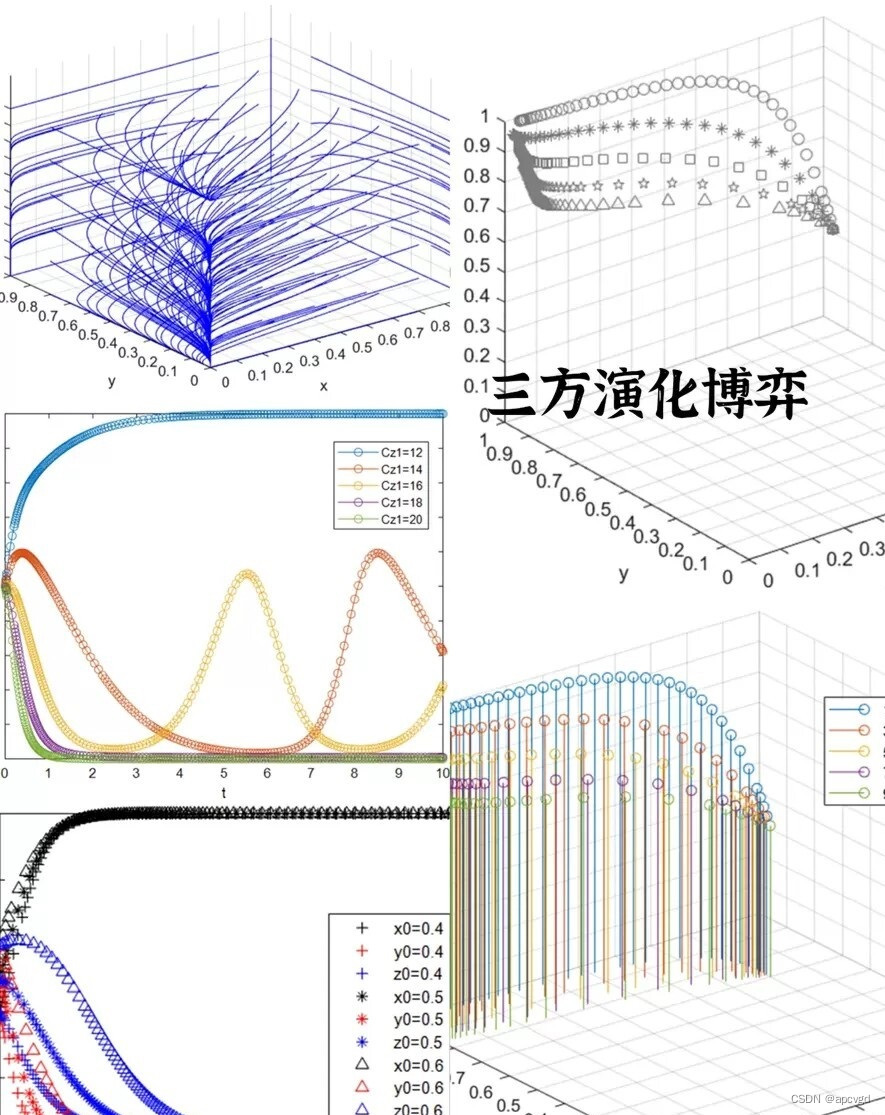
接下来，我们来介绍三方演化博弈。这种博弈模型是在两个对手之外，引入了第三方角色，从而增加了博弈的复杂度。在这个模型中，每个对手会根据其策略来进行行动，但是由于第三方的存在，他们的策略会相互影响，从而导致整个演化博弈的结果与双方演化博弈有很大不同。在这个模型中，我们同样可以使用代数的方法分析其稳定点，并通过绘制相位图的方式进行可视化。同时，我们也可以通过Matlab的仿真代码来模拟整个演化过程，并对其进行更详细的分析。

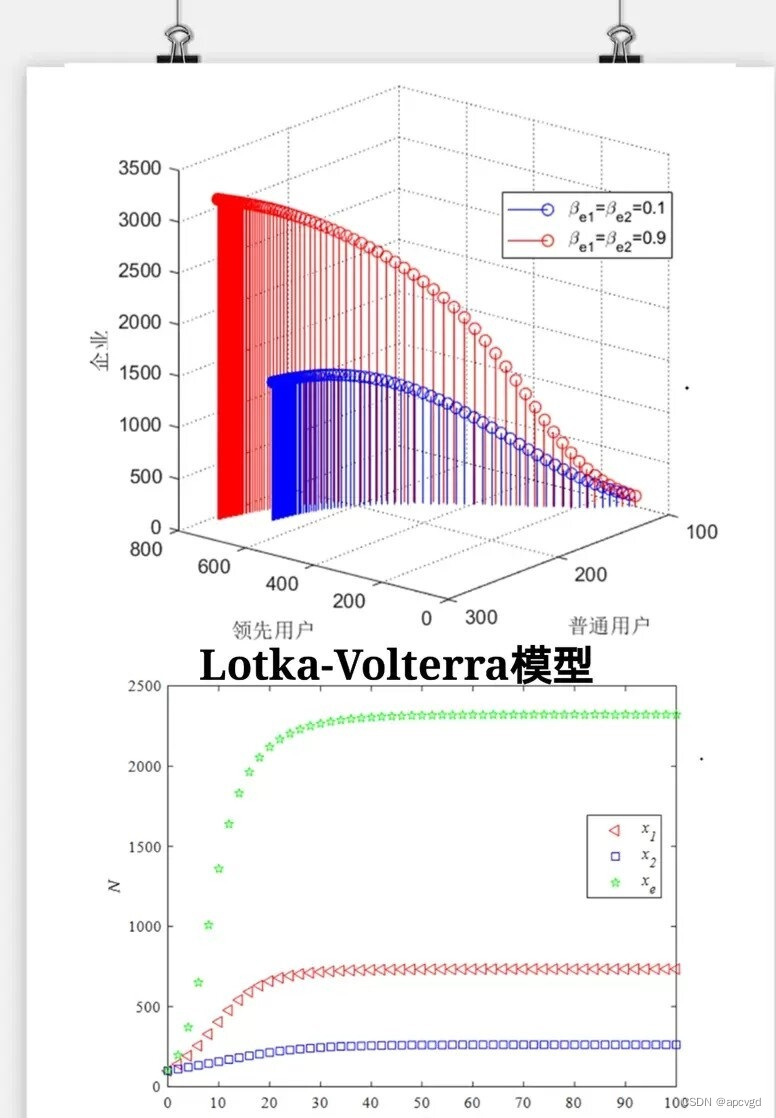
最后，让我们来介绍Lotka-Volterra模型。这个模型是一种生态系统模型，用于描述食物链上物种数量的动态演化过程。在这个模型中，每个物种会根据其食物来源和天敌数量来进行自我调节。通过这个模型，我们可以更好地了解生态系统中不同物种之间的相互关系，从而更好地保护和维护生态环境的平衡。

综上所述，演化博弈理论在现代社会中已经得到了广泛应用，并且在计算机科学和人工智能领域中发挥了重要作用。通过使用Matlab，我们可以更好地分析和仿真双方演化博弈、三方演化博弈和Lotka-Volterra模型，从而更好地理解这些模型的本质和应用。希望本文能够为读者提供有价值的参考，并对演化博弈理论的研究和应用有所帮助。
标题：MATLAB实现双及三方演化博弈的稳定性分析及仿真

一、引言

演化博弈论是一种动态的博弈理论，其主要关注的是博弈的长期动态行为。其中，双及三方演化博弈作为其重要分支，广泛应用于生态、经济、社会等许多领域。对于这种博弈，我们常常借助数学工具进行稳定点分析，并通过仿真技术绘制相位图，以直观地理解其动态行为。本文以MATLAB为平台，详细介绍如何实现双及三方演化博弈的稳定性分析及仿真。

二、双方演化博弈

在双方演化博弈中，我们通常有两个策略的博弈方，分别为策略A和策略B。在每一次的博弈中，两个博弈方根据一定的规则选择策略并获得收益。随着时间的推移，博弈方会根据自身的收益和对手的策略调整自己的策略。

对于这样一个博弈，我们可以通过微分方程来描述其动态行为。设博弈方的策略为x和y，其收益函数为P(x,y)，则其动态方程可以表示为：

dx/dt = P(x,y) - <P(x,y)> - x <P(x,y)>

dy/dt = Q(x,y) - <Q(x,y)> - y <Q(x,y)>

其中，< > 表示在所有策略分布下的平均值。

对于这样一个动态方程，我们可以利用MATLAB进行数值模拟。首先，我们需要定义收益函数P(x,y)，然后利用ODE求解器（如ode45）对动态方程进行求解。通过这样的方法，我们可以得到策略x和y随时间的变化曲线，以及不同策略的稳定点。

三、三方演化博弈

在三方演化博弈中，我们通常有三个策略的博弈方，分别为策略A、策略B和策略C。在每一次的博弈中，三个博弈方根据一定的规则选择策略并获得收益。随着时间的推移，博弈方会根据自身的收益和对手的策略调整自己的策略。

对于这样一个博弈，我们同样可以通过微分方程来描述其动态行为。设博弈方的策略为x、y和z，其收益函数为P(x,y,z)，则其动态方程可以表示为：

dx/dt = P(x,y,z) - <P(x,y,z)> - x <P(x,y,z)>

dy/dt = Q(x,y,z) - <Q(x,y,z)> - y <Q(x,y,z)>

dz/dt = R(x,y,z) - <R(x,y,z)> - z <R(x,y,z)>

其中，< > 表示在所有策略分布下的平均值。

对于这样一个动态方程，我们同样可以利用MATLAB进行数值模拟。首先，我们需要定义收益函数P(x,y,z)，然后利用ODE求解器（如ode45）对动态方程进行求解。通过这样的方法，我们可以得到策略x、y和z随时间的变化曲线，以及不同策略的稳定点。

四、Lotka-Volterra模型

Lotka-Volterra模型是一种经典的生物种群演化模型，其灵感来源于生态学中的捕食与被捕食关系。在这个模型中，我们通常有两个种群，分别为捕食者（策略A）和被捕食者（策略B）。在每一次的交互中，两个种群根据一定的规则获得收益。随着时间的推移，种群会根据自身的收益和对手的种群密度调整自己的繁殖和死亡速率。

对于这样一个模型，我们同样可以通过微分方程来描述其动态行为。设种群的密度为x和y，其收益函数为P(x,y)，则其动态方程可以表示为：

dx/dt = αx[βx + γy] - λx - αRx + φMy - δx²

dy/dt = εx[γy + δx] - λy - αMy + φRx - δy²

其中，α表示繁殖速率，β表示自我繁殖的收益，γ表示从被捕食者获得的收益，λ表示自然死亡速率，R表示人为捕获的速率，φ表示被捕食者的繁殖速率，M表示被捕食者的最大密度，δ表示自我繁殖和被捕食的收益饱和系数。

对于这样一个动态方程，我们同样可以利用MATLAB进行数值模拟。首先，我们需要定义收益函数P(x,y)，然后利用ODE求解器（如ode45）对动态方程进行求解。通过这样的方法，我们可以得到两个种群的密度随时间的变化曲线，以及不同策略的

资料来源于
https://www.liruan.net/963.html