题意
一个序列的权值定义为ϕ(lcm(a1,a2,...,ak))\phi(lcm(a_1,a_2,...,a_k))ϕ(lcm(a1,a2,...,ak))
求所有长度为kkk的,每个值ai≤na_i \leq nai≤n的序列的权值积
分析
首先使用min-max容斥把lcm改写成gcd
ϕ(S)=∏T⊂Sϕ(gcd(T)(−1)∣T∣−1)ans=∏a1=1n∏a2=1n..∏ak=1n∏T⊂{a1,a2,...,ak}ϕ(gcd(T)(−1)∣T∣−1)
\phi(S)=\prod_{T \subset S}\phi(gcd(T)^{(-1)^{|T|}-1})\\
ans=\prod_{a_1=1}^n\prod_{a_2=1}^n..\prod_{a_k=1}^n\prod_{T \subset \{a_1,a_2,...,a_k\}}\phi(gcd(T)^{(-1)^{|T|}-1})\\
ϕ(S)=T⊂S∏ϕ(gcd(T)(−1)∣T∣−1)ans=a1=1∏na2=1∏n..ak=1∏nT⊂{a1,a2,...,ak}∏ϕ(gcd(T)(−1)∣T∣−1)
把T拿出来枚举
ans=∏w=1k∏a1=1n∏a2=1n..∏aw=1nϕ(gcd(a1,a2,...,aw))(−1)w−1Ckwnk−w
ans=\prod_{w=1}^k \prod_{a_1=1}^n\prod_{a_2=1}^n..\prod_{a_w=1}^n\phi(gcd(a_1,a_2,...,a_w))^{(-1)^{w-1}C_{k}^{w}n^{k-w}}
ans=w=1∏ka1=1∏na2=1∏n..aw=1∏nϕ(gcd(a1,a2,...,aw))(−1)w−1Ckwnk−w
先计算
res=∏a1=1n∏a2=1n..∏aw=1nϕ(gcd(a1,a2,...,aw))
res=\prod_{a_1=1}^n\prod_{a_2=1}^n..\prod_{a_w=1}^n\phi(gcd(a_1,a_2,...,a_w))
res=a1=1∏na2=1∏n..aw=1∏nϕ(gcd(a1,a2,...,aw))


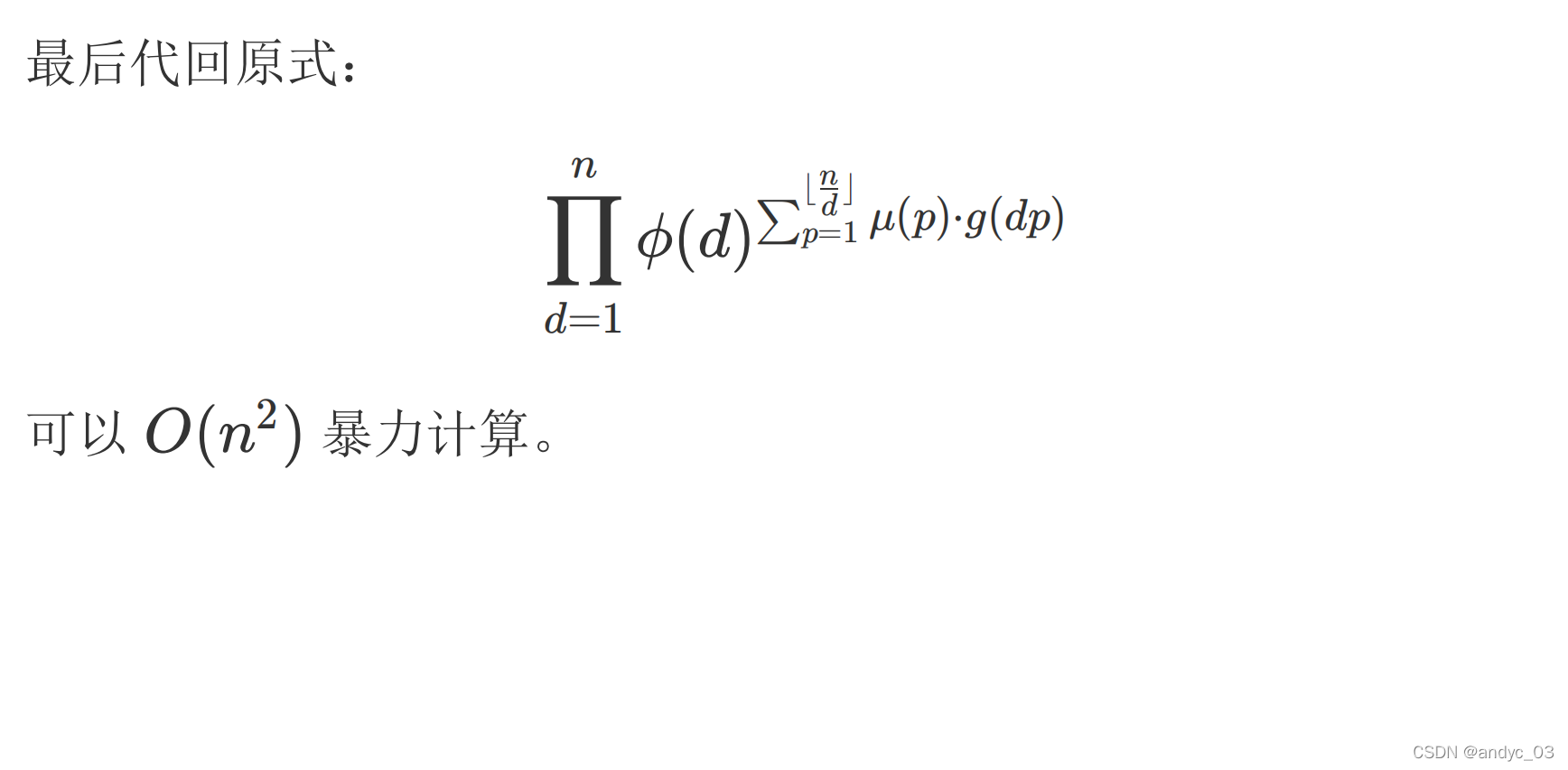





 本文探讨了一种计算长度为k的序列权值积问题,通过将lcm转换为gcd并利用min-max容斥原理,给出了详细的公式推导过程。关键步骤包括将序列权值表示为gcd的组合,并通过枚举子集来求积。
本文探讨了一种计算长度为k的序列权值积问题,通过将lcm转换为gcd并利用min-max容斥原理,给出了详细的公式推导过程。关键步骤包括将序列权值表示为gcd的组合,并通过枚举子集来求积。
















 1242
1242

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








