【行列式】

【性质】
1.单位矩阵的行列式为1
2.交换两行要变号
3.有两行一样的话行列式为0
用上面的第二条,将这两行交换,加了符号实际上却未变,就是0
4.线性性
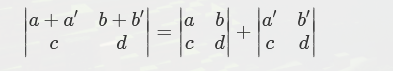
5.用矩阵的一行加上另一行的倍数,行列式不变
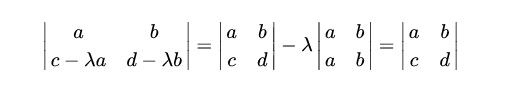
【求法】
利用高斯消元的方式,再加上上面的性质加以辅助即可
我们对于 A 进行消元,然后记录操作对于行列式的影响,最后得到上三角矩阵,行列式就是对角线乘积,如果消不出来那么返回 0
【矩阵树定理】
矩阵树定理是用来求一个无向图有多少生成树的方法
设这个图的邻接矩阵为G,度数矩阵为D(只有对角线上有值,为d[i])
定义一个图的Kirchhoff矩阵K=D−A
可以证明这个矩阵去掉任意一行和一列,行列式的值不变
且这个值就是生成树的个数
【例题1】P4111 [HEOI2015]小 Z 的房间
【习题1】P4336 [SHOI2016]黑暗前的幻想乡
这个题是无向图的板子+简单的一点容斥 sol.
【带权的矩阵树定理】
正常的带权的矩阵树求的是所有生成树的边权乘积之和
构建方法就是把邻接矩阵的1改成对应边权即可
【例题2】P3317 [SDOI2014]重建
这道题目就是普通的利用带权的性质,构造了一下邻接矩阵的值
【有向图矩阵树定理】
这个就是简单改造一下,边的邻接矩阵不变
度数矩阵分类讨论,外向树度数只统计入度,内向图度数只统计出度
然后注意这里这就不能任意去掉一行一列了,一定要去掉起始点(root)的那一行和列
【例题3】P4455 [CQOI2018]社交网络
【变形——带权矩阵树定理】
这是一类特别的问题,求所有生成树的边权和的和
不同于一般的生成树带权的积的和,我们无法直接利用普通的行列式计算了
这时,我们就可以考虑利用计算贡献的方式
先算出整张图的生成树个数tot
然后枚举m条边,删除它求一下生成树个数cnt,我们知道当前边的贡献为$(tot-sum)*w[i]$
这样的做时间复杂度较大,为$O(n^3m)$
我们继续考虑优化
我们可以自行构造行列式内记录的信息来维护,我们给行列式每个位置赋值(x,y)
表示方案数为x,所有方案的边权的和的和为y
然后我们依然是计算乘法
(a,b)*(c,d)=(a*c,a*d+b*c)
这样我们第二维度的数就是答案
考虑我们在高斯消元的时候需要除法,根据乘法定义(a,b)*(c,d)=(a*c,a*d+b*c),推出(a*c,a*d+b*c)/(a,b)=(c,d)然后计算就行了,这个的没什么实际意义,就相当于一个逆运算
【例题4】P6624 [省选联考 2020 A 卷] 作业题
这道题需要简单莫比乌斯反演,枚举一下因数,然后就是裸的了





 这篇博客介绍了行列式的性质和计算方法,重点讲述了矩阵树定理及其在无向图生成树计数中的应用。同时,讨论了带权矩阵树定理在解决带权生成树问题上的角色,以及如何处理有向图的情况。文章通过实例解析了如何利用这些理论解决实际问题,如P4111[HEOI2015]小Z的房间和P3317[SDOI2014]重建等题目,并提到了一种优化算法来降低时间复杂度。
这篇博客介绍了行列式的性质和计算方法,重点讲述了矩阵树定理及其在无向图生成树计数中的应用。同时,讨论了带权矩阵树定理在解决带权生成树问题上的角色,以及如何处理有向图的情况。文章通过实例解析了如何利用这些理论解决实际问题,如P4111[HEOI2015]小Z的房间和P3317[SDOI2014]重建等题目,并提到了一种优化算法来降低时间复杂度。
















 2932
2932

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








