一、算法
Key points:
- 决策树是一个分类算法,分类结果是离散值(对应输出结果是连续值的回归算法);
- 有监督的分类算法;
- 是一种贪婪算法,生成的每一步都是局部最优值
- 容易over fitting
- noise影响不大
- 空间划分,通过递归的方法把特征空间划分成不重叠的矩形
例子 (from Machine Learning in Action):
判断是否是Fish,有两个特征Can survive without coming to surface?和 Has flippers?

最后实现的决策树为:
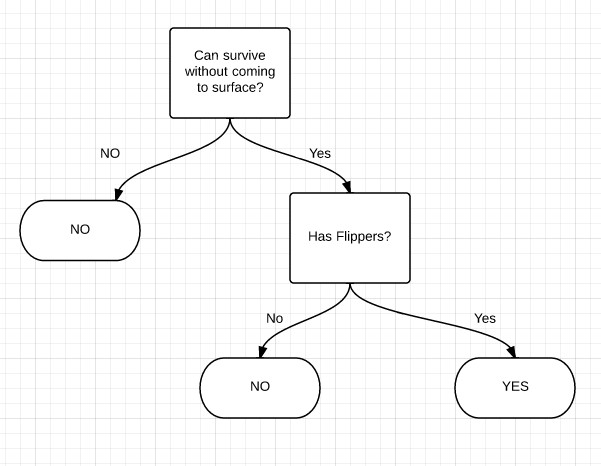
生成决策树时要考虑的问题:
- How should the training records be split?
每次split的时候,都要挑选一个最佳的特征。
The method developed for selecting the best split are often based on the degree of impurity of the child node.
例如:集合{'yes':10,'no':0}的不纯洁度最低,集合{'yes':5,'no':5}不纯洁度最高,显然要挑不纯度低 的特征;描述不纯度的方法有以下几种:
信息熵
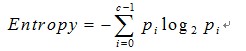
Gini
Gini impurity is the expected error rate if one of the results from a set is randomly applied to one of the items in the set.(集体智慧编程) ???
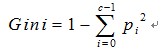
计算出每个子集的不纯度后,再计算split以后总不纯度。与split前的不纯度相比较
信息增益(information gain)就是指信息熵的有效减少量

选择差值最大的
例如:原集合为[yes,yes,no,no,no]
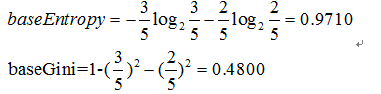
选择“surface”, split后的集合为:[yes,yes,no]和[no,no]
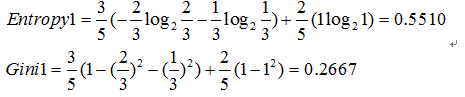
选择"Flippers", split后的集合为:[yes,yes,no,no]和[no]
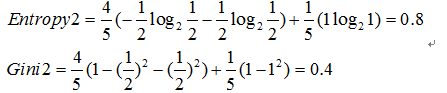
最后选择差值最大的,即”surface“
- How should the splitting procedure stop?
当所有的records属于同一类,即分类完毕;或者features用完了
或者information gain=0??
当达到以上两种情况时,往往会发生过拟合,见以下
如何处理过拟合的问题:
- 设定一个阈值,该阈值可以是决策树高度,节点实例个数,信息增益值等,该节点成为叶节点
- 该叶节点持有其数据集中样本最多的类或者其概率分布
-
首先构造完整的决策树,允许决策树过度拟合训练数据
- 对置信度不够的节点的子树用叶节点或树枝来替代
- 该叶节点持有其子树的数据集中样本最多的类或者其概率分布
什么时候需要剪枝:
- 数据噪音,因此有的分类不准
- 训练数据量少,或者不具有代表性
- 过拟合
ID3, C4.5, C5.0, CART
ID3 1986年 Quilan
选择具有最高信息增益的属性作为测试属性
01 | ID3(DataSet, featureList): |
03 | - 如果当前DataSet中的数据都属于同一类,则标记R的类别为该类 |
04 | - 如果当前featureList集合为空,则标记R的类别为当前DataSet中样本最多的类别 |
06 | # 从featureList中选择属性(选择Gain(DataSet,F)最大的属性) |
07 | # 根据F的每一个值v,将DataSet划分为不同的子集DS,对每一个Ds: |
09 | - 如果DS为空,节点C标记为DataSet中样本最多的类别 |
10 | - 如果DS不为空,节点C=ID3(DS,featureList-F) |
C4.5 1993年 by Quilab(对ID3的改进)
- 信息增益率(information gain ratio)
- 连续值属性
离散化处理:将连续型的属性变量进行离散化处理,形成决策树的训练集
- 把需要处理的样本按照连续变量的大小从小到大进行排序
- 假设该属性对应的不同的属性值一共有N个,那么总共有N-1个可能的候选分割阈值点,每个候选的分割阈值点的值为上述排序后的属性值中两两前后元素的中点
- 用信息增益率选择最佳划分
- 处理缺少属性值的一种策略是赋给它节点t所对应的训练实例中该属性的最常见值
- 复杂一点的办法是为每个可能值赋一个概率
- 最简单的办法是丢弃这些样本
- 后剪枝(基于错误剪枝EBP-Error Based Pruning)
C5.0 1998年
加入了Boosting算法框架
CART (Classification and Regression Trees)
- 二叉树不易产生数据碎片,精确度往往会高于多叉树,所以在CART算法中采用二元划分
- 分类目标:Gini指标、Towing、order Towing
- 连续目标:最小平方残差、最小绝对残差
- 用独立的验证数据集对训练集生长的树进行剪枝
分类树:
01 | CART_classification(DataSet, featureList, alpha,): |
03 | 如果当前DataSet中的数据的类别相同,则标记R的类别标记为该类 |
04 | 如果决策树高度大于alpha,则不再分解,标记R的类别classify(DataSet) |
06 | 标记R的类别classify(DataSet) |
07 | 从featureList中选择属性F(选择Gini(DataSet, F)最小的属性划分,连续属性参考C4.5的离散化过程(以Gini最小作为划分标准)) |
08 | 根据F,将DataSet做二元划分DS_L 和 DS_R: |
11 | C_L= CART_classification(DS_L, featureList, alpha); |
12 | C_R= CART_classification(DS_R featureList, alpha) |
回归树
01 | CART_regression(DataSet, featureList, alpha, delta): |
03 | 如果当前DataSet中的数据的值都相同,则标记R的值为该值 |
04 | 如果最大的phi值小于设定阈值delta,则标记R的值为DataSet应变量均值 |
05 | 如果其中一个要产生的节点的样本数量小于alpha,则不再分解,标记R的值为DataSet应变量均值 |
07 | 从featureList中选择属性F(选择phi(DataSet, F)最大的属性,连续属性(或使用多个属性的线性组合)参考C4.5的离散化过程 (以phi最大作为划分标准)) |
08 | 根据F,将DataSet做二元划分DS_L 和 DS_R: |
09 | 如果DS_L或DS_R为空,则标记节点R的值为DataSet应变量均值 |
11 | C_L= CART_regression(DS_L, featureList, alpha, delta); |
12 | C_R= CART_regression(DS_R featureList, alpha, delta) |
分类树与回归树的差别在于空间划分方法一个是线性一个是非线性
二、python实现
如何在python中存储一棵决策树. 如果每个特征只有两种选择,就是一棵二叉树。但往往不局限于二叉树。
- 采用字典数据结构,如上例中的决策树最后可以表示成这样:
{'no surfacing': {0: 'no', 1: {'flippers': {0: 'no', 1: 'yes'}}}}
新建一个结点:{'label':{}}, split以后{'label':{cond1:{},cond2:{},cond3:{}}},如果满足if语句,{}就是一个label,如果不满足,就建结点
1 | class decisionNode(object): |
2 | def __init__(self,test_cond=-1,value=None,labels=None,trueBranch=None,falseBranch=None): |
3 | self.test_cond = test_cond |
6 | self.trueBranch=trueBranch |
7 | self.falseBranch=falseBranch |
输入训练样本:
04 | dataSet = [[1, 1, 'yes'], |
09 | features = ['no surfacing','flippers'] |
11 | return dataSet, features |
用递归的方法建造决策树,代码如下:
用字典表示:
01 | def treeGrowth(dataSet,features): |
02 | classList=[example[-1] for example in dataSet] |
03 | if classList.count(classList[0])==len(classList): |
05 | if len(dataSet[0])==1: |
06 | return classify(classList) |
08 | bestFeat=findBestSplit(dataSet) |
09 | bestFeatLabel=features[bestFeat] |
10 | mytree={bestFeatLabel:{}} |
11 | featValues=[example[bestFeat] for example in dataSet] |
12 | uniqueFeatValues=set(featValues) |
13 | del(features[bestFeat]) |
14 | for values in uniqueFeatValues: |
15 | subDataSet=splitDataSet(dataSet,bestFeat,values) |
16 | mytree[bestFeatLabel][values] =treeGrowth(subDataSet,features) |
用节点类表示:
01 | def treeGrowth(dataSet,features): |
02 | classList=[example[-1] for example in dataSet] |
04 | if classList.count(classList[0])==len(classList) : |
05 | return decisionNode(labels=classList[0]) |
08 | return decisionNode(labels=classify(classList)) |
11 | bestFeature = findBestSplit(dataSet) |
13 | bestFeatureLabel=features[bestFeature] |
15 | root.test_cond=bestFeatureLabel |
17 | featureValues=[example[bestFeature] for example in dataSet] |
18 | uniqueFeatureValues =set(featureValues) |
19 | del(features[bestFeature]) |
21 | for value in uniqueFeatureValues: |
22 | subDataSet=splitDataSet(dataSet,bestFeature,value) |
24 | trueChild=treeGrowth(subDataSet,features) |
25 | root.trueBranch=trueChild |
27 | falseChild=treeGrowth(subDataSet,features) |
28 | root.falseBranch=falseChild |
找出子集合中的大多数:
1 | def classify(classList): |
4 | if vote not in classCount.keys(): |
7 | sortedClassCount = sorted(classCount.iteritems(), key=operator.itemgetter(1), reverse=True) |
8 | return sortedClassCount[0][0] |
找出最佳特征:
01 | def findBestSplit(dataSet): |
02 | numFeatures=len(dataSet[0])-1 |
03 | baseEntropy = calcShannonEnt(dataSet) |
06 | for i in range(numFeatures): |
07 | featValues=[example[i] for example in dataSet] |
08 | uniqueFeatValues=set(featValues) |
10 | for val in uniqueFeatValues: |
11 | subDataSet=splitDataSet(dataSet,i,val) |
12 | prob=len(subDataSet)/float(len(dataSet)) |
13 | newEntropy+=prob*calcShannonEnt(subDataSet) |
14 | if (baseEntropy- newEntropy)>bestInfoGain: |
15 | bestInfoGain=baseEntropy- newEntropy |
01 | def splitDataSet(dataSet,feat,values): |
03 | for featVec in dataSet: |
04 | if featVec[feat]==values: |
05 | reducedFeatVec=featVec[:feat] |
06 | reducedFeatVec.extend(featVec[feat+1:]) |
07 | retDataSet.append(reducedFeatVec) |
10 | def calcShannonEnt(dataSet): |
11 | numEntries = len(dataSet) |
13 | for featVec in dataSet: |
14 | currentLabel = featVec[-1] |
15 | if currentLabel not in labelCounts.keys(): |
16 | labelCounts[currentLabel]=0 |
17 | labelCounts[currentLabel]+=1 |
20 | for key in labelCounts: |
21 | prob=float(labelCounts[key])/numEntries |
23 | shannonEnt-=prob*log(prob,2) |
三、R实现
01 | creatDataSet<-function(){ |
02 | dataSet<-data.frame(c(1,1,1,0,0),c(1,1,0,1,1),c("yes","yes","no","no","no")) |
03 | names(dataSet)<-c("no surfacing","flippers","results") |
07 | setClass("decisionNode", |
24 | findBestSplit<-function(dataSet){ |
25 | classList<-dataSet$result |
26 | numFeatures<-length(dataSet)-1 |
27 | baseEntropy<-calcShannonEnt(dataSet) |
29 | for(i in range(1:numFeatures)){ |
31 | for(j in range(unique(dataSet[,i]))){ |
32 | subDataSet<-splitDataSet(dataSet,i,j) |
33 | prob<-length(subDataSet[,1])/length(dataSet[,1]) |
34 | newEntropy<-newEntropy+prob*calcShannonEnt(subDataSet) |
36 | if((baseEntropy-newEntropy)>bestInfoGain){ |
37 | bestInfoGain<-baseEntropy-newEntropy |
44 | calcShannonEnt <- function(dataSet){ |
46 | sum<-length(dataSet[,1]) |
47 | labelCounts<-as.data.frame(table(dataSet[,end])) |
49 | for(i in range(1:length(labelCounts[,1]))){ |
50 | prob<- labelCounts[i,-1]/sum |
52 | shannonEnt<-shannonEnt-prob*log(prob,2) |
59 | splitDataSet<- function(dataSet,feature,value){ |
60 | subDataSet<-dataSet[which(dataSet[,feature]==value),] |
61 | subDataSet[,feature]<-NULL |
65 | treeGrowth<-function(dataSet){ |
66 | classList<-dataSet$result |
67 | if(length(which(classList==classList[1]))==length(classList)) return (new("decisionNode",labels=classList[1])) |
68 | if(length(dataSet)==1) return (new("decisonNode",labels=classify(classList))) |
69 | root<-new("decisionNode") |
71 | bestFeature<-findBestSplit(dataSet) |
72 | bestFeatureLabel<-names(dataSet)[bestFeature] |
73 | root@test_cond<-bestFeatureLabel |
74 | uniqueValues<-unique(dataSet[bestFeature]) |
75 | for(i in range(uniqueValues)){ |
77 | subDataSet<-splitDataSet(dataSet,bestFeature,i) |
80 | trueChild<-treeGrowth(subDataSet) |
81 | root@trueBranch<-trueChild |
83 | falseChild<-treeGrowth(subDataSet) |
84 | root@falseBranch<-falseChild |





 本文深入解析决策树算法,包括分类与回归树的工作原理、构建决策树的方法、过拟合处理策略以及如何在Python中实现。文章涵盖信息熵、基尼不纯度、信息增益等概念,并通过实例展示决策树的构建过程。
本文深入解析决策树算法,包括分类与回归树的工作原理、构建决策树的方法、过拟合处理策略以及如何在Python中实现。文章涵盖信息熵、基尼不纯度、信息增益等概念,并通过实例展示决策树的构建过程。


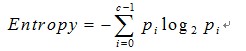
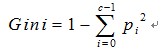

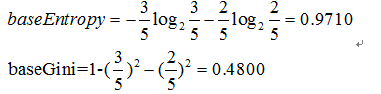
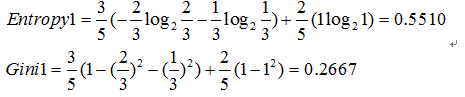
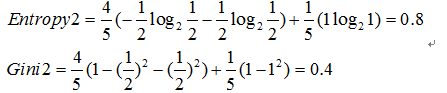
















 4510
4510

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








