LGS谐振传感器振荡电路设计

基于石英（LGS）的谐振式压力-温度传感器的 振荡器电路设计

Abstract

为使用新开发的兰加石（LGS）压电晶体测量压力 和温度，提出了一种闭环频率跟踪电子电路。环境力和热量作用 在LGS晶体上会导致其谐振频率发生变化。所提出的闭环电子电 路能够跟踪谐振频率的变化，并通过频率变化的差异来测量压力 和温度。谐振电路的稳态振荡条件已通过分析推导并进行了实验 验证。实验装置包括一个基于运算放大器的谐振电路，连接到放 置在双侧径向力加载装置和温度控制器浴中的兰加石压电晶体。
施加在LGS晶体上的径向力会在其基本机械振动模式（C模式）
中产生频率偏移。同样，温度变化会在其第二机械振动模式（B
模式）中产生频率偏移。通过两个独立的闭环谐振电路分别测量 两种不同的被测参数。当外部未知压力改变LGS晶体上的力时， 会增加压电材料的固有特性变化，从而改变基本振荡谐振频率。
闭环谐振电路会跟踪谐振频率的变化，并根据外部压力强度使L
GS以新的谐振频率振动。对于温度引起的频率跟踪测量也采用类 似的过程。所提出的频率跟踪电子电路概念简单，且发现其具有 高灵敏度和线性度。

Keywords — langasite(LGS) piezo crystals, resonant sensor, oscillator electronics, pressure and temperature measurement

一、引言

对用于谐振传感器的高频、高稳定、低功耗振荡器电路 的设计需求大幅增加。振荡器电子设计的复杂性也非常大 ，因为我们开始转向高频谐振传感器的应用[1]。谐振传感 器是一种具有在共振状态下振动元件的装置，其输出频率 （即机械共振频率）会随着质量、压力、温度、加速度等 物理参数的变化而变化[2, 3]。为了使谐振结构保持在共振 状态，各种振荡器
已被采用，可分为两种主要类型：谐波振荡器和非线性或 弛豫振荡器。最常见的谐波振荡器形式是使用带有反馈回 路和频率选择性电子储罐网络的电子放大器[4, 5]。这种反 馈振荡器网络可以根据反馈回路中使用的频率选择性滤波
器类型进行分类，即相移振荡器和维恩电桥振荡器使用RC
网络[6]，哈特利、科皮茨和克拉普振荡器使用LC储罐电路 [7]，而佩尔兹振荡器电路则使用压电晶体。压电晶体（例 如石英）被用作谐振器，因为它具有非常高的Q值，并且 比调谐电路具有更好的温度稳定性，因此晶体振荡器的频 率稳定性比LC或RC振荡器要好得多。在本文中，设计了 一种简单的闭环电子电路，使用运算放大器使压电晶体结
构保持共振。这项工作中使用了一种新开发的朗加石（LG S）压电晶体，用于设计基于谐振的压力和温度传感器[8, 9
]。谐振传感器的优点是其高稳定性、高分辨率和准数字输
出。各种谐振传感器已被研究，其中一些已实现商业化[10
, 11]。还提出了用于力感测的谐振传感器，其中施加的应 力有效地增加了谐振器结构的刚度，从而导致谐振器固有 频率的增加[12]。在[13]中研究了通过频率传感电路实时监 测压电材料刚度和质量变化引起的谐振频率偏移。然而， 到目前为止，由于操作电子电路的复杂性和对高Q值设计 方面的考虑，谐振传感器在商业传感器产品中仍很少见。
这项工作的技术原创性在于为新开发的基于LGS晶体的 压力和温度测量提出了一个简单的闭环谐振器电子电路。
所提出的振荡方法是通过利用LGS压电晶体的谐振特性来 实现的。在确立谐振测量方法的概念之后，建立了一个分 析模型，用于预测稳定状态振荡的条件。为了证明所提出 电路的有效性，采用了两种不同类型的谐振传感应用。关 系
978-1-5090-2091-1/16/$31.00 ©2016 IEEE
振荡频率与压力和温度之间的关系是根据实验结果建立的 。

在第二部分中，介绍了振荡器的工作原理。第三部分详 细描述了分析模型，第四部分讨论了评估电子电路，第五 部分给出了结论。

二、电子技术的工作原理

所提出的谐振器电子电路包括一个高频运算放大器和无
源电阻、电容元件。所提出的谐振器电路的原理图如图1
所示。LGS压电体的底部电极和R2C2低通滤波器并联连接 到运算放大器的非反相输入端。放大器的电压增益保持大 于或等于1，运算放大器的输出连接到LGS压电晶体的顶部 电极。当系统开启时，压电晶体对噪声作出响应并产生一
个小电压，该电压被放大器用来建立稳定的振荡条件[14, 1
5]。压电晶体在其串联谐振频率fs下工作。这种所提出的 振荡器电子电路的工作原理基于维恩电桥振荡器的原理。
通过设计反馈电阻RT、RB以及R2C2的值以提供所需的增 益和相位移，使LGS压电晶体在其第一谐波振动频率（压 力）下振荡。为了测量温度，采用类似的方法对第二谐波 频率进行处理。闭环电子电路的稳定性由对应泛音频率的 Q值决定。闭环谐振电路会跟踪谐振频率的变化，并在压 力或温度在压电材料上施加应变时，使LGS以新的谐振频 率振动。

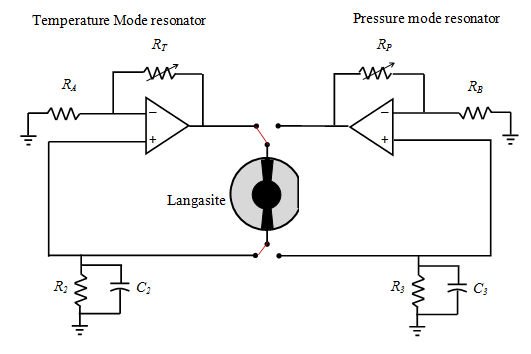
LGS压电晶体通过上述频率跟踪谐振器电子电路被设计 为在C模和B模频率下共振。C模频率用于压力传感应用， B模频率用于温度传感应用。该电路的性能进行了理论评 估并实验验证。

三、分析模型

所有图1中的Langasite压电晶体都被其压电等效电路所 替代，带有电气参数模型的闭环谐振器电子电路如图2所 示。

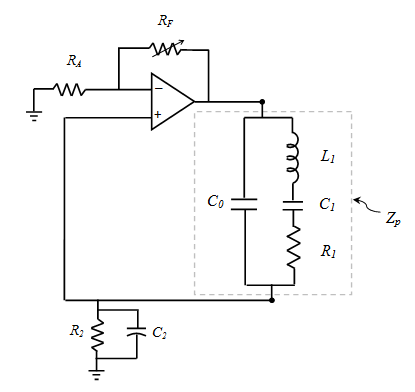
晶体有两个由零相位移表征的谐振频率。第一个是串联
谐振频率fs，第二个是并联/反谐振频率fa。串联谐振频率f
s的公式为[16]：

$$
f_s = \frac{1}{2\pi\sqrt{L_1 C_1}}
$$

在谐振频率fs时，感抗和容抗相等并相互抵消XC1=XL1
。因此，压电元件输入和输出之间的相位差为零度。输出 电压的幅度最大，约为输入电压的三分之一（1/3）。由于
感抗XC1和容抗XL1相互抵消，旁路电容XC0的电抗与电阻R
1并联。

在谐振时，XC0>> R1的值为零，因此晶体在非常接近 R1
的值时在电路中表现出电阻性。压电晶体在谐振时的这种 电阻性行为进一步简化了振荡器电路，并表现为维恩电桥 振荡器网络。

压电晶体的复数阻抗定义为[7]：

$$
X_C = \frac{1}{j2\pi f C_S}
$$

$$
X_1 = R_1 + j2\pi f L_1 + \frac{1}{j2\pi f C_1}
$$

将XC0和X1并联使用可得到

$$
Z_p = \frac{X_{C0} \cdot X_1}{X_{C0} + X_1}
$$

正反馈网络由压电等效元件（L1C1R1和C0）组成，连接到
并联的R2C2网络，基本上形成一个高通滤波器（with
压电元件的无限机械谐波振动连接到一个低通滤波器，产 生一个非常选择性的二阶频率依赖带通滤波器，在选定频 率fs处具有高Q值。在谐振频率fs时，串联电容（C1）和电 感（L1）的感抗为零，因此压电元件像一个窄带通滤波器 ，阻止任何其他频率的输入信号。因此，在压电元件的输 出信号中只有一个谐振频率，即串联谐振频率（fs）。在 高频时，并联电容（C2）的感抗非常低，因此这个并联连 接的电容在输出端起到短路作用，避免捕捉到更高模式的 谐振频率。然而，在这两个极端之间，通过R1和R2分压网 络的帮助，输出电压达到最大值，并与谐振频率（fs）一 起振荡。

所提出的振荡器电路需要在频率fs处生成正弦波形。为 此，R2、C2、RA和RF需要根据晶体串联谐振频率fs进行计 算。R2的值被选择为等于运动臂电阻R1，即R1=R2。通过 使用R2的值，C2如下推导得出。

$$
C_2 = \frac{1}{2\pi f_s R_2}
$$

对于正弦振荡开始，振荡电路的电压增益必须等于或大 于1，(Av ≥ 1)（增益取决于特定模式的Q值）[17]。对于 非反相运算放大器配置，此值由RA和RF的反馈电阻网络 设定，其表达式为：

$$
A_v = \frac{V_{out}}{V_{in}} = 1 + \frac{R_F}{R_A}
$$

一旦振荡器建立稳态振荡条件，闭环谐振电路就会跟踪 谐振频率的变化，并在压力或温度变化时，用新的谐振频 率驱动压电元件。

四、电子设备的评估

所提出的闭环电子电路的频率跟踪能力用于压力和温度 测量。基于兰加石晶体的压力和温度传感器在实验室中设
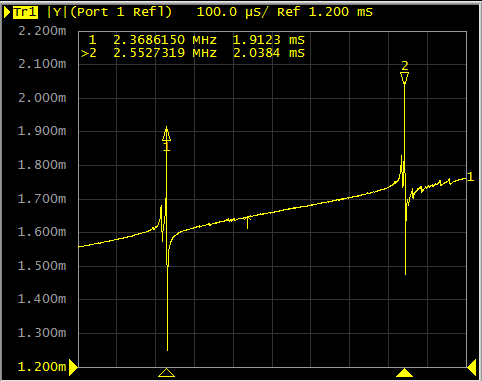
计和开发。为此分析，使用了直径为13mm、厚度为0.7mm 的LGS压电谐振器（܇܆ܟܔ ૠ૞0/૝૞0）。首先，使用KEYSIGTH E5016B网络分析仪测量了LGS晶体的C模式和B模式 的频率及其电气等效参数。实验测得的压电晶体电气参数 通过代入方程（1）、（4）和（5）来推导解析的谐振频 率和阻抗。压电晶体的谐振频率和电气参数见表I。压电等 效电路和其频率响应的网络分析仪结果，显示了双模态， 见图3和4。LGS压电体的C模式谐振频率为2.3MHz，B模 式为2.5MHz。基于C和B模式的谐振频率，
谐振电子电路参数已确定，其值见表II。利用表II中的数值
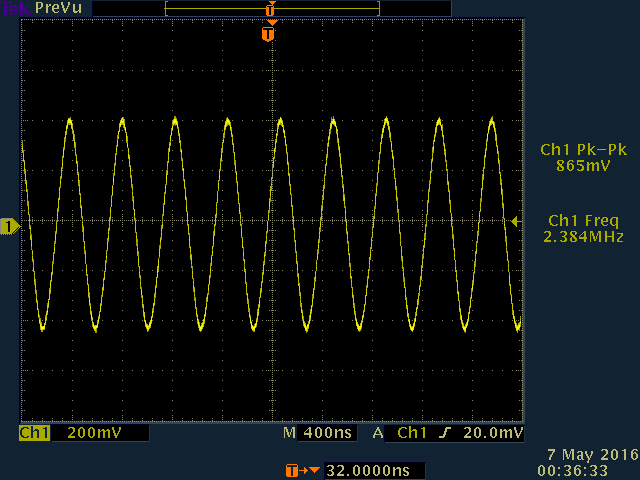
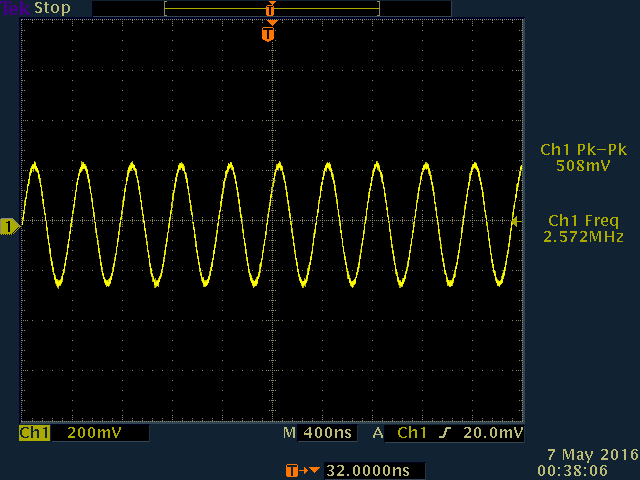
，在面包板上设计了电路，电路的图片如图5所示。使用Tektronix TDS 3054C数字磷光示波器测量了2.3MHz和2.5MHz处的闭环谐波振荡频率，结果如图6和图7所示。

表I. LGS晶体的电气性能

Symbol	Description	C- Mode	B- Mode	Units
R1	Motional arm resistor of piezo	1.721154	1.403897	kȍ
C1	Motional arm capacitor of piezo	6.801997	5.642864	fF
L1	Motional arm inductor of piezo	663.6814	688.8203	mH
C0	Stray capacitor of piezo	109.3541	111.4095	pF
Fa	Analytical resonant frequency	2.370000	2.554300	MHz
Fe	Experimental resonant frequency	2.3686776	2.5527390	MHz

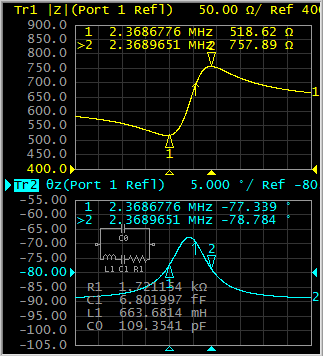
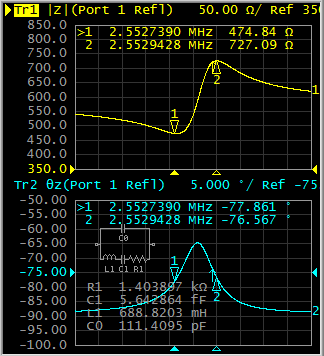
表II.增益和低通滤波器的电阻和电容值

Parameter	C Mode-2.3MHz	B Mode- 2.5MHz
Resistor- RF	1.1 kŸ	1.1 Ÿ
Resistor – RA,B	1 kŸ	1 kŸ
Resistor – R2	1.2 kŸ	0.8 kŸ
Capacitor– C2	12.3pF	12.3pF

A. Pressure measurement

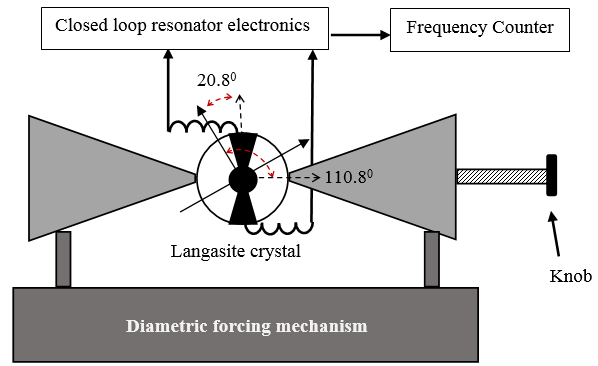
最初，所提出的电子设备的频率跟踪能力被实验性地评估用于压力传感应用。为此分析使用了压电晶体的C模式 （2.3MHz）。LGS压电晶体被放置在径向力加载机构之间 ，如图8所示。对LGS晶体施加径向力会在其基本机械振动模式中产生频率偏移。频率偏移通过所提出的闭环谐振器电子设备进行测量，频率差与未知压力相关。径向力加载机构的照片如图9所示，相应的力-频率关系如图10所示。
从图10可以看出，LGS压电晶体对力的响应良好，所提出的电子设备确实能够很好地跟踪频率偏移。

B. Temperature measurement

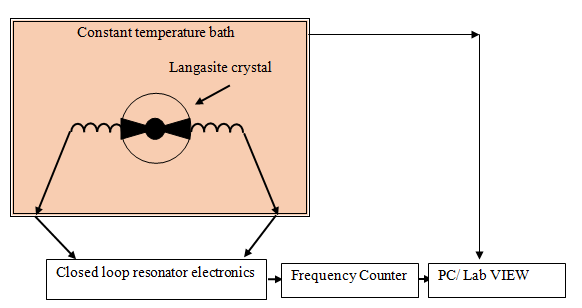
同样，所提出的电子设备的频率跟踪能力也针对温度传感应用进行了评估。为了方便起见，温度变化分析也使用了压电晶体的C-模式（2.3MHz）谐振频率。LGS压电晶体放置在恒温槽中，如图11所示。施加在LGS晶体上的温度会导致频率偏移。该频率偏移通过电子设备进行测量，频率差与环境温度相关。图12显示了带有LSG压电晶体的恒温槽照片，图13显示了压电晶体的温度依赖性频率变化 。从图13可以看出，所提出的电子设备在频率跟踪应用中具有很高的灵敏度。

五．结论

本文报告了一种用于基于谐振的压力和温度传感器的简单闭环谐振器电子电路。Langasite（LGS）压电晶体的机械和电气特性在开环状态下进行了测量，以确定所需的谐振频率模式。该谐振器进一步与设计的振荡器电子电路在闭环中成功进行了测试。稳态振荡条件和使用滤波器的操作频率选择性通过分析方法得到，并经过实验验证。由于采用了高频晶体谐振器，压力和温度的分辨率得到了提高 。所提出的反馈电子电路结构简单，可轻松应用于任何使用压电谐振器的测量。