KDD'24 | 合约广告中大规模多重线性约束库存分配问题的高效局部搜索算法

▐ 摘要

合约广告（Guaranteed Delivery Advertising）是在线广告的重要组成部分，合理的合约库存分配机制直接提升客户需求和平台收入。随着广告客户需求的越来越多样化和精细化，在业务场景中经常出现媒体偏好需求，即适合投放在指定媒体的广告在该媒体上分配的比例应该大于另一些不适合在该媒体投放的广告。然而，这些需求涉及到非凸的多重线性约束，会给合约广告的库存分配带来挑战，而数学规划求解器或现有基于约束的启发式求解方法无法在约束时间内产生高质量的解。本文提出一种局部搜索的框架来解决这个难题，该框架包含两阶段的搜索模式，并且集成了四种新的针对非线性约束设计的算子。实验结果表明，相比于其它算法或者求解器，我们的算法能够在业务要求的约束时间内产生高质量的解，并且该算法具备通用性，可以处理其它业务场景中存在的非线性约束，未来可以应用到更多类似的场景中。基于该项工作整理的论文已被KDD 2024接收，欢迎阅读交流。

论文：An Efficient Local Search Algorithm for Large GD Advertising Inventory Allocation with Multilinear Constraints

作者：Xiang He, Wuyang Mao, Zhenghang Xu, Yuanzhe GU, Yundu Huang, ZHONGLIN ZU, Liang Wang, Mengyu Zhao, Mengchuan Zou

1. 背景介绍 

合约广告是在线广告行业的重要组成部分，它在品牌的在线商业营销和推广中起着至关重要的作用。广告库存的分配是合约广告的关键组成部分。广告客户通常会在广告投放日期的几个月或几周前与平台签订合同，以预先锁定所需的广告展示次数。合同中明确规定了在特定定向条件下（如人群、频次控制、城市、渠道）的广告展示数量。如果库存过度出售，可能导致无法完成合同中的展示数量目标，平台需要进行赔偿；而库存少售卖则会损害平台的收入。在以往的广告库存分配工作中，研究的重点仅限于包含线性约束。通常会利用线性约束的性质，利用对偶和KKT条件，快速解决问题。然而，这些算法只能处理线性或凸性约束。随着商业需求的不断扩大，越来越多的细化需求被提出，其中一些需求可以自然地表达为非线性约束，并且在数学形式上是非凸形式。举例来说，假设一个客户有两种产品，一个是护肤精华液，一个是耳机，并指定美妆app作为护肤精华液的重点媒体，相对于耳机来说。广告主希望护肤精华液在美妆app上的分配比例比耳机更大，使其更多地集中展示在合适的媒体上。

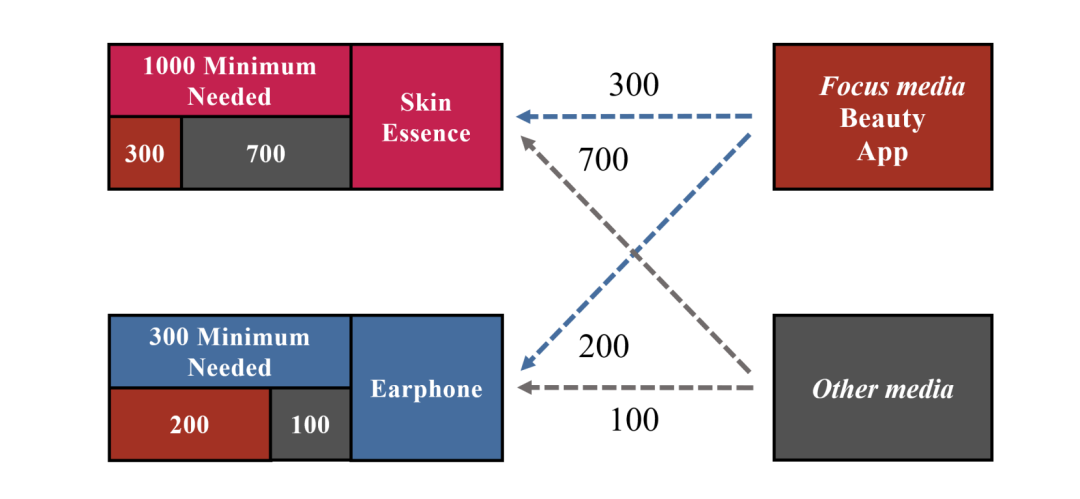
由于现有求解器和方法的效率或能力不足以处理商业场景中的这些非凸约束，这就需要探索新技术和新算法来有效解决这些问题。针对此问题，我们做了以下工作：

1）首次提出解决带有非线性约束的库存分配问题，将其建模为一个包含多线性约束的整数规划问题。

2）设计了一种轻量级局部搜索求解器LS-IMP来解决这个问题。提出了四种新的邻域操作来处理多线性约束，并设计了两种切换模式，以快速找到问题的近似最优解。LS-IMP可以轻松处理商业场景中的一般多线性约束。

3）我们在真实的在线广告应用数据上对保证交付库存分配进行了实验。实验结果表明，我们的求解器在更多实例中满足了要求，并在商业指标上具有更高质量的分配结果，优于数学规划或基于约束的启发式求解器。

2. 问题建模

2.1 二部图建模

GD广告库存分配问题是计算新合同的最大可能展示量（库存），同时确保展示量满足发布商和广告商的需求约束。该问题可以使用二部图来描述，它可以使用二部图表示，如下图所示。在左侧，供给节点集对应于基本维度（城市 媒体 操作系统）的展示次数。在右侧，需求节点集对应于销售系统中的合同。其中，需求节点代表新合同，而其他需求节点代表现有合同。决策变量表示从供给分配到需求的展示次数。

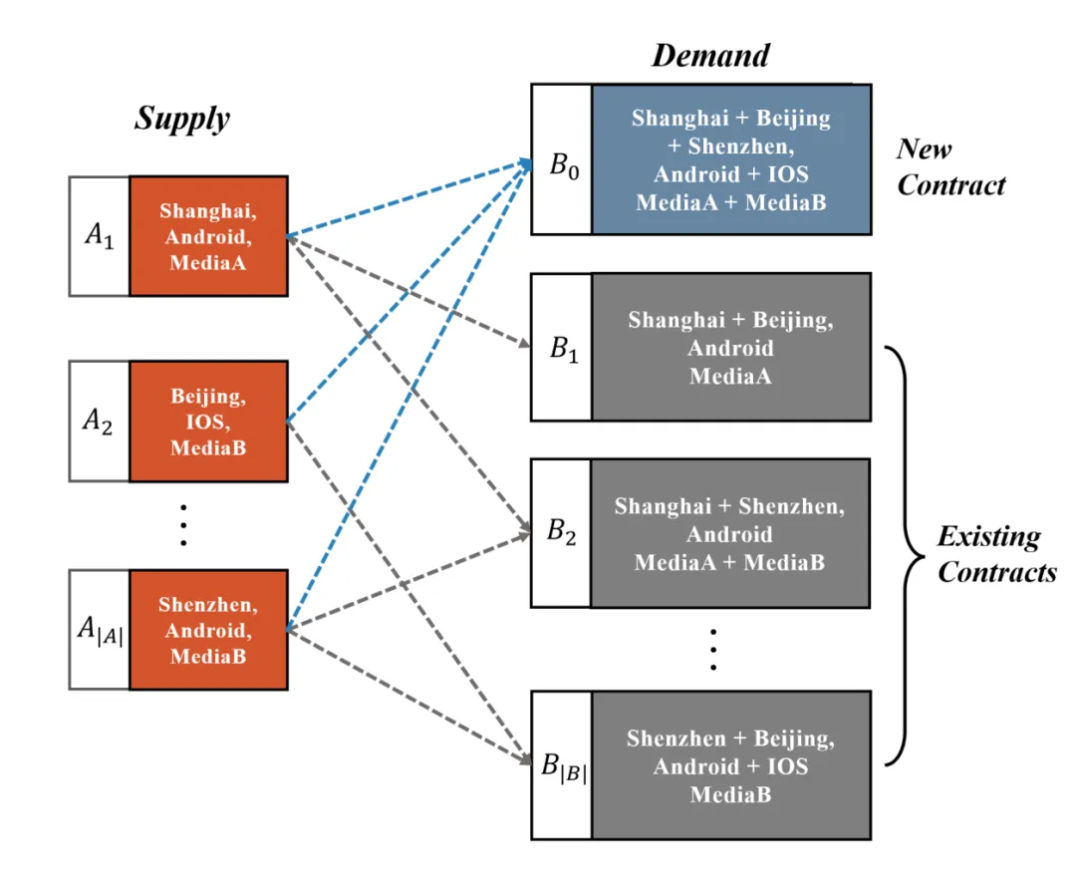
问题的目标是求解以最大化分配给新合同的展示次数，并满足三种约束条件：

1）供给约束：每个供给节点的总分配量不应超过其供给量；

2）需求约束：分配到某个需求节点的展示次数不应少于其需求；

3）Focus约束：在关注媒体上，合同的关注比例不得低于另一个合同。此约束涉及同一广告主的两个合同和及一组选定的指定媒体集，代表相比的关注媒体。然后要求合同和在供给集上的关注比例符合广告主的优先级要求：合同在上的关注比例应大于合同的关注比例。

我们使用邻接矩阵（）来表示供应节点和需求节点之间的连接，如果供应节点 和需求节点 之间存在连接，则

2.2 整数多重线性规划

整数多重线性规划 (IMP) 问题的形式如下：