目录
1.定积分
定积分是微积分中的一个重要概念,用于求解函数在某个区间上的累积效应或面积。
1.1定积分的定义
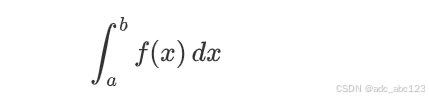
表示函数 f(x)在区间 [a,b]上的累积效应或面积。定积分的定义可以通过以下步骤来理解:

说明:

1.2定积分的几何意义
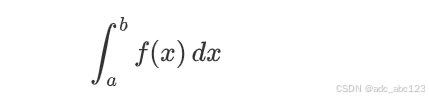
的几何意义是函数 f(x) 在区间 [a,b]上的曲线下面积。具体来说:
-
如果 f(x)≥0,则定积分表示曲线下方的面积。
-
如果 f(x)≤0,则定积分表示曲线上方的面积的负值。
1.3定积分的性质
- 线性性质
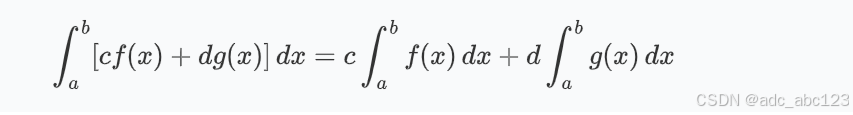
其中 c 和 d 是常数。
- 区间可加性
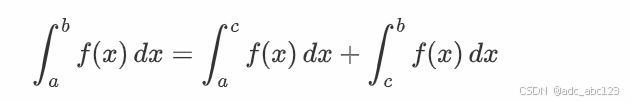
其中 a≤c≤b。
- 积分上下限交换
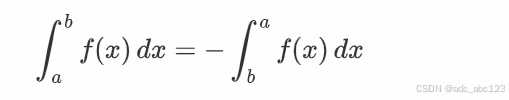
- 定积分中值定理
如果函数 f(x) 在闭区间 [a,b] 上连续,则存在 c∈[a,b],使得:
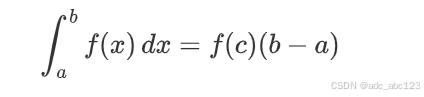

1.4微积分基本公式

- 第一部分

- 第二部分

1.5定积分换元法
步骤:

2.多元函数
2.1二元极限
2.1.1二元极限定义

2.1.2二元极限的几何意义
当点 (x,y)从任意方式趋近于点 (a,b) 时,函数 f(x,y) 的值趋近于 L。换句话说,函数图像在二维平面的点 (a,b)附近趋近于一个三维立体平面上的点 (a,b,L)。可将(a,b)想象为(a,b,L)投影在二维平面的点。
如果 (x,y)从不同方式趋近于点 (a,b),函数 f(x,y) 的值不相等,则表示 f(x,y) 不存在。
例一:
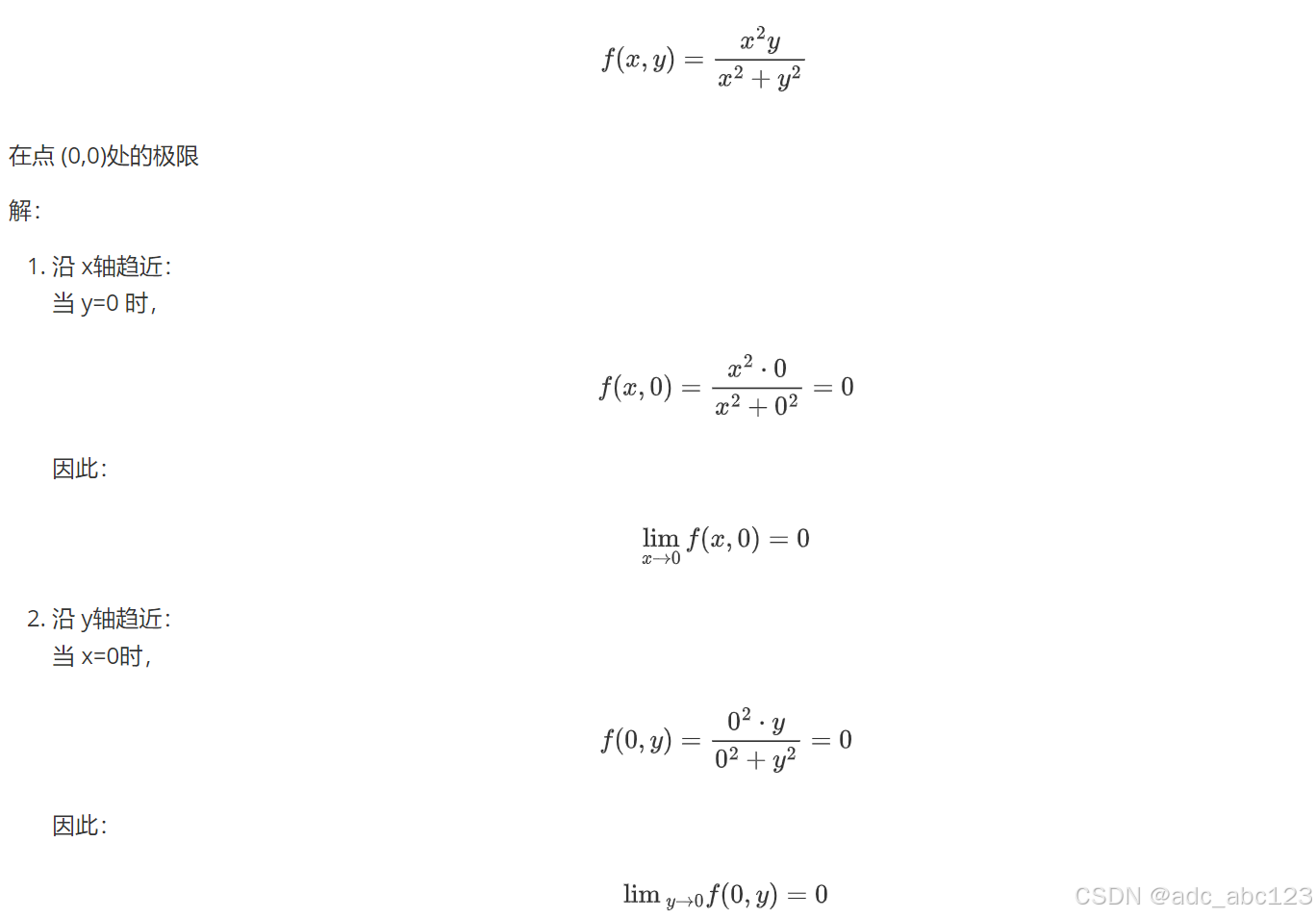

例二:
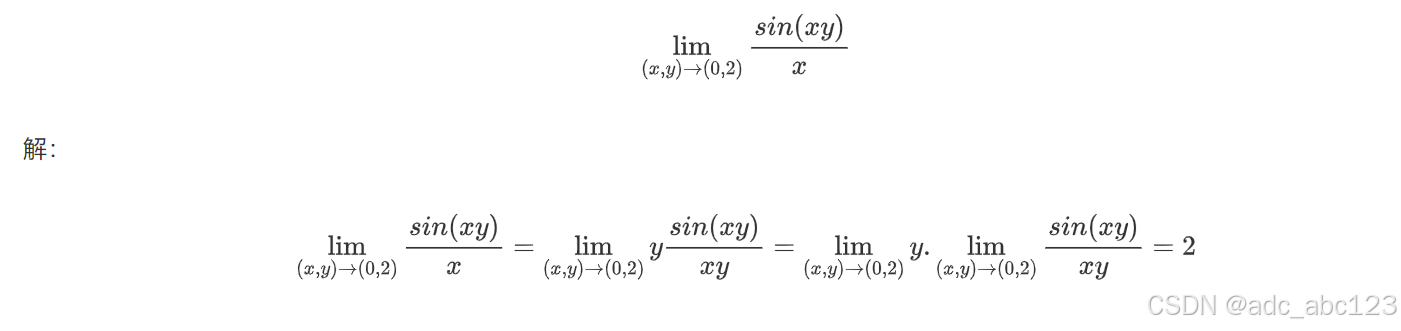
2.2偏导数
偏导数是多元函数求导的一种形式,表示在多个自变量中,当其中一个自变量改变而其他自变量保持不变时函数值的变化率。
这实质上是将其他自变量视为常数,然后按照单变量函数求导的方法进行运算。
2.2.1偏导数的定义
设函数 f(x,y) 在点 (x0,y0) 的某个邻域内有定义。如果极限:

2.2.2偏导数的计算方法
2.对于二元函数z=f(x,y),求z对x的偏导数时,将y看作常量,对x求导;求z对y的偏导数时,将x看作常量,对y求导。
2.3全微分
2.3.1全微分的定义
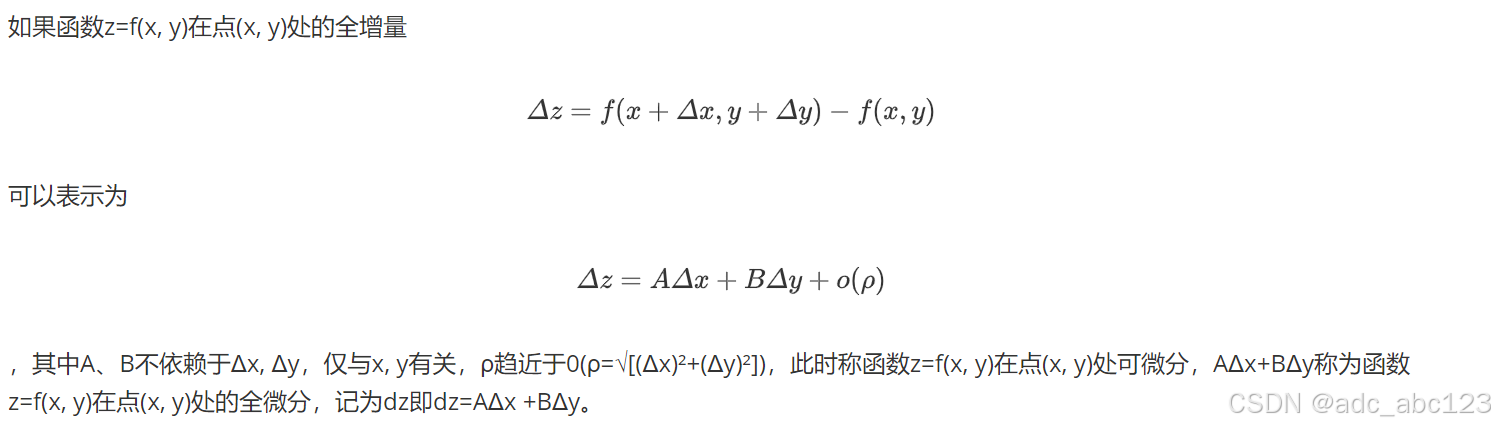

2.3.2近似计算

2.4梯度
梯度是一个向量,表示多元函数在某一点处的最大变化率和变化方向。
2.4.1梯度的定义
设 f(x1,x2,…,xn)是一个定义在 Rn(n维欧几里得空间) 上的多元函数,函数 f在n维向量点 a=(a1,a2,…,an)处的梯度定义为:
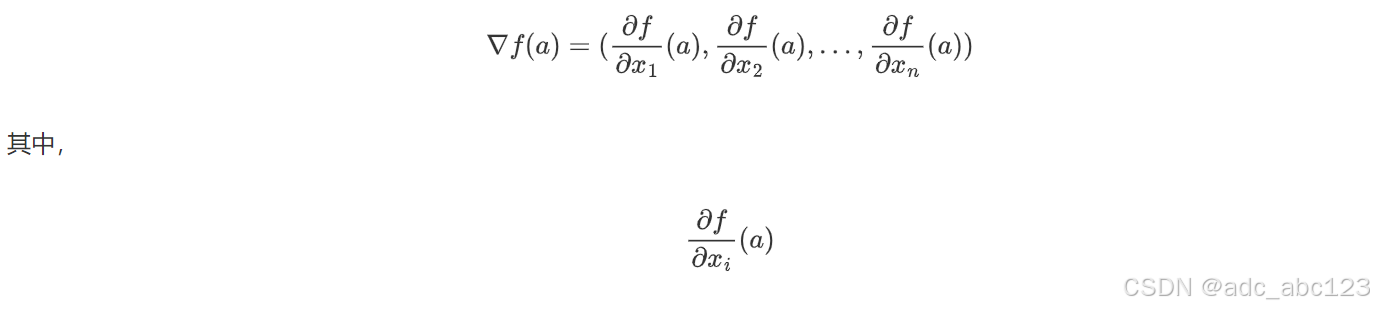
是函数 f 在点 a 处对第 i 个自变量的偏导数。
2.4.2梯度的性质
- 最大变化率
梯度 ∇f(a) 的方向是函数 f在点 a 处变化率最大的方向。
- 变化率
梯度 ∇f(a) 的大小(模)是函数 f 在点 a 处沿梯度方向的变化率。
沿梯度方向是是函数 f在点 a 处变化率增加最大的方向;沿梯度
2.4.3梯度下降
梯度下降是一种优化算法,用于寻找多元函数的最小值。其基本思想是沿着函数的负梯度方向逐步更新参数,以减少函数值。
反方向是是函数 f在点 a 处变化率减小最大的方向;沿梯度垂直方向函数 f在点 a 处变化率为0。
算法步骤


2.4.4学习率
学习率 η是一个重要的超参数,控制着每次更新的步幅。选择合适的学习率对于梯度下降算法的性能至关重要:
-
学习率过大
如果步幅过大,算法可能会“跳过”最优解,导致在最优解附近来回震荡。
-
学习率过小
可能导致算法收敛速度过慢。
示例:

2.5二重积分
2.5.1二重积分的定义

2.5.2二重积分的几何意义
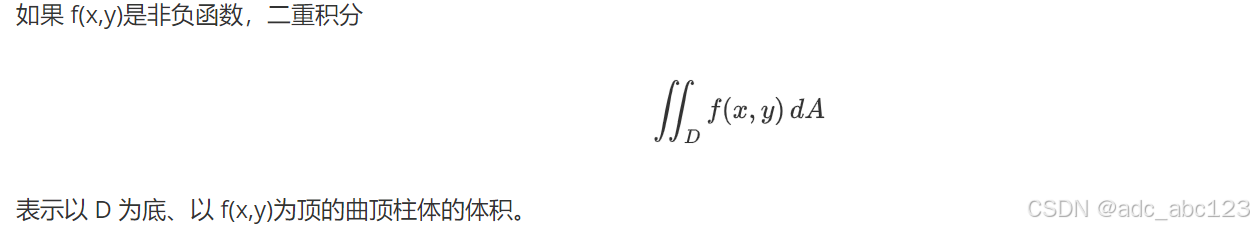
2.5.3直角坐标系求二重积分

2.5.4极坐标系求二重积分

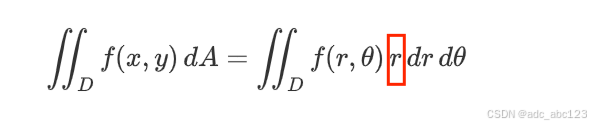
注意:转换为极坐标系的二重积分中需要多加一个dr ,易忘。
3.三角函数
3.1.基本定义
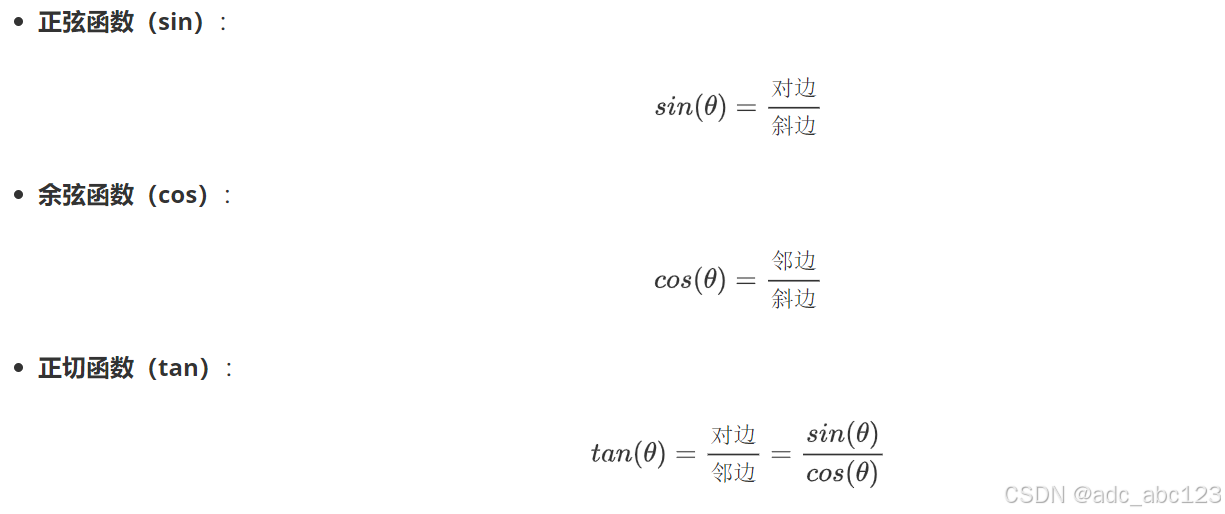
3.2基本关系
3.2.1毕达哥拉斯恒等式
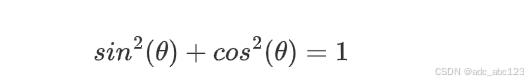
这个恒等式可以从直角三角形的勾股定理推导出来。
3.2.2商数关系
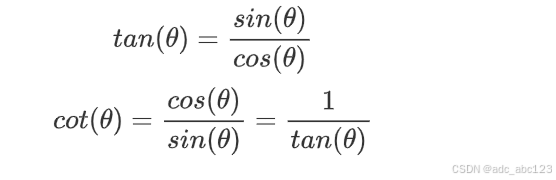
3.2.3倒数关系
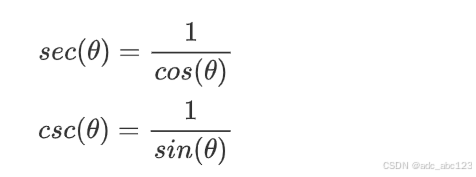
3.3三角函数的周期性
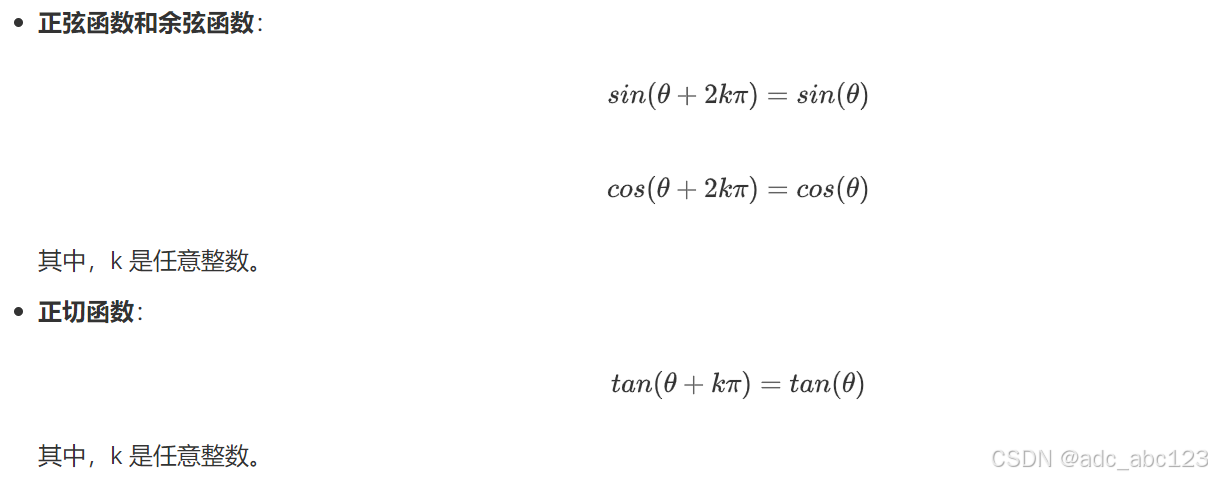
3.4三角函数的对称性
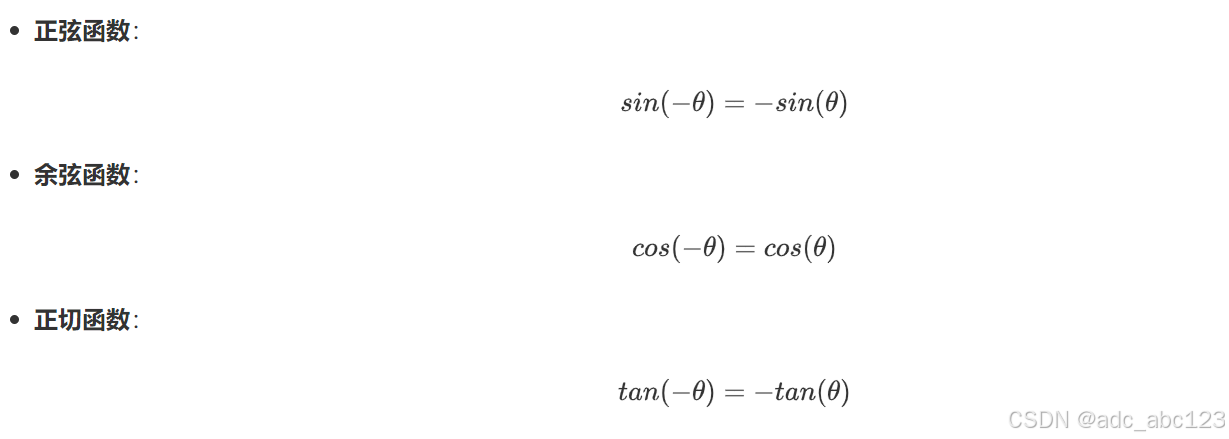
3.5三角函数的和差公式
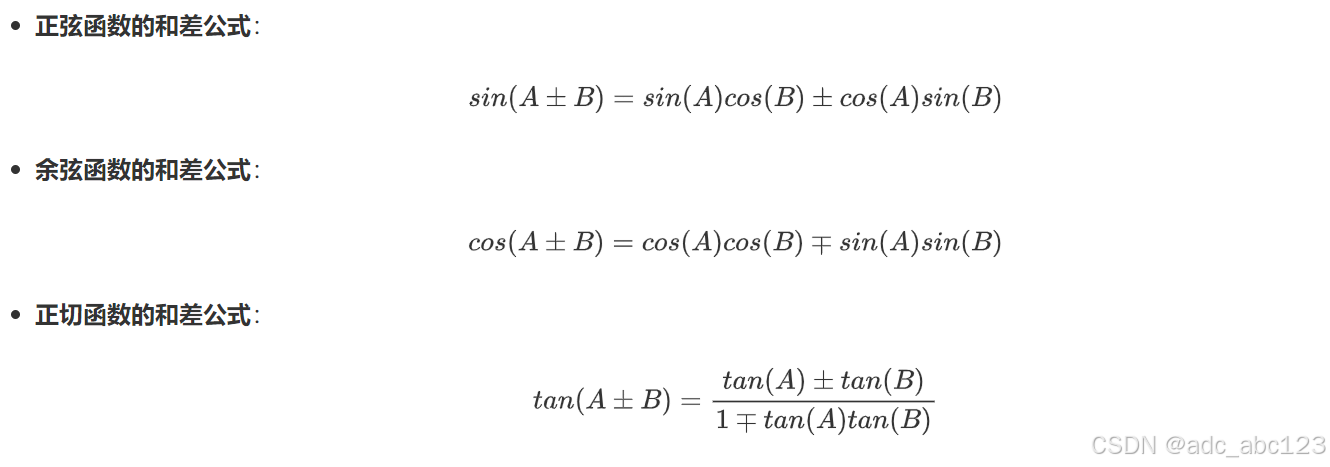
3.6三角函数的倍角公式
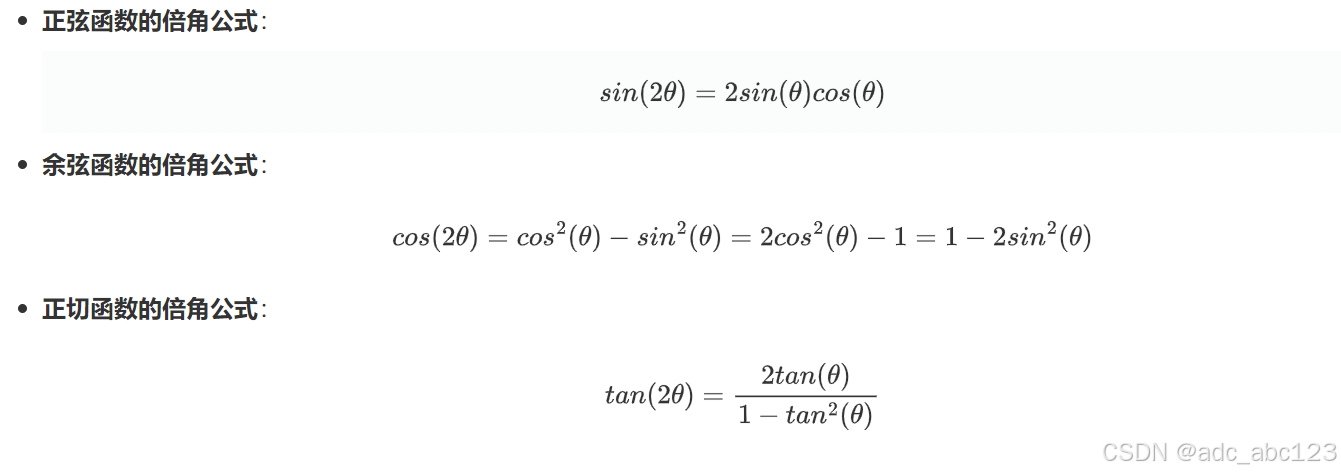
2.7三角函数的半角公式
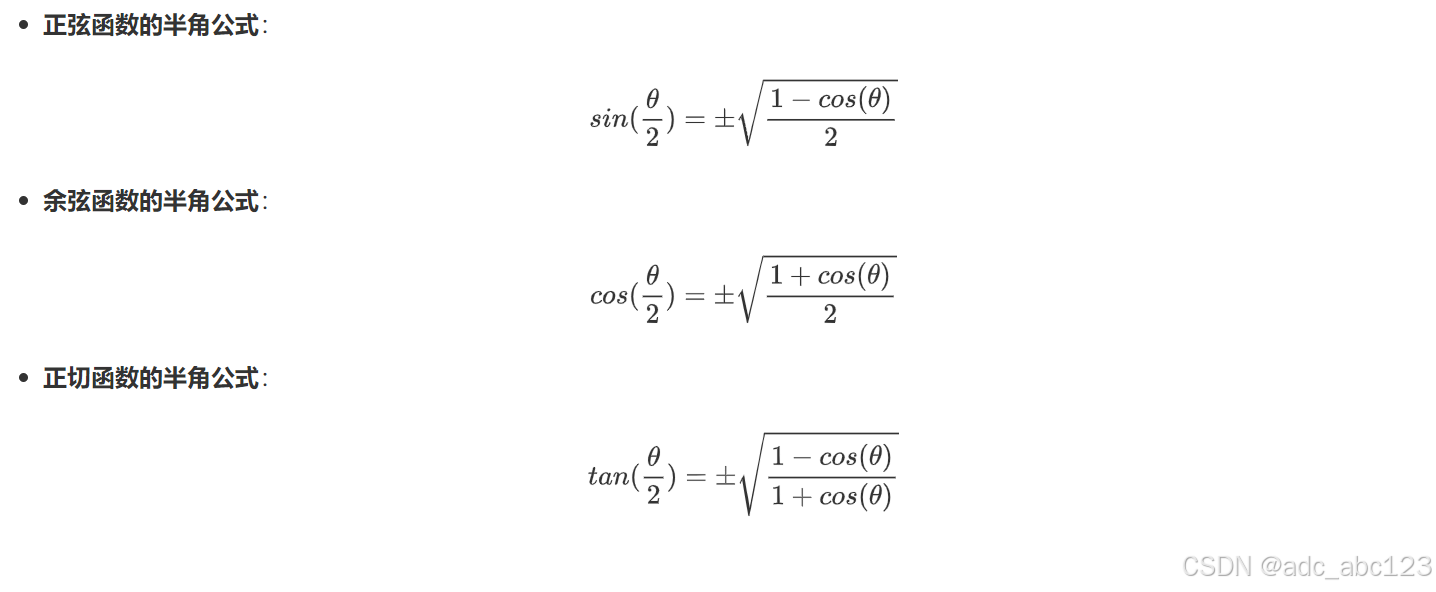




















 1632
1632

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








