图像的正交变换在数字图像的处理与分析中起着很重要的作用,被广泛应用于图像增强、去噪、压缩编码等众多领域。本文手工实现了二维离散傅里叶变换和二维离散余弦变换算法,并在多个图像样本上进行测试,以探究二者的变换效果。
1. 傅里叶变换
实验原理
对一幅图像进行离散傅里叶变换(DFT),可以得到图像信号的傅里叶频谱。二维 DFT 的变换及逆变换公式如下:
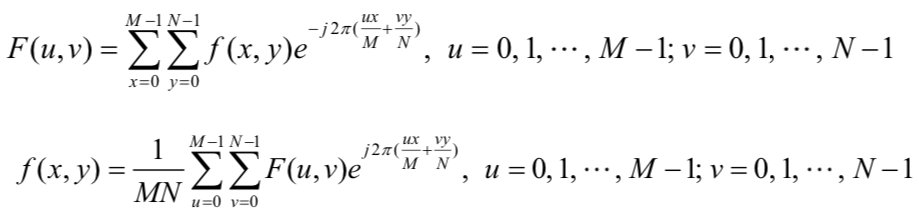
DFT 尽管解决了频域离散化的问题,但运算量太大。从公式中可以看到,有两个嵌套的求和符号,显然直接计算的复杂度为 O ( n 2 ) O(n^2) O(n2) 。为了加快傅里叶变换的运算速度,后人提出快速傅里叶变换(FFT),即蝶形算法,将计算 DFT 的复杂度降低到了 O ( n log n ) O(n\log n) O(nlogn)。
FFT 利用傅里叶变换的数学性质,采用分治的思想,将一个 N N N 点的 FFT,变成两个 N / 2 N/2 N/2 点的 FFT。以一维 FFT 为例,可以表示如下:
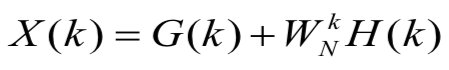
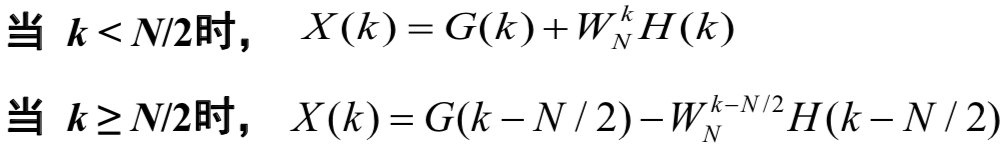
其中, G ( k ) G(k) G(k) 是 x ( k ) x(k) x(k) 的偶数点的 N / 2 N/2 N/2 点的 FFT, H ( k ) H(k) H(k) 是 x ( k ) x(k) x(k) 的奇数点的 N / 2 N/2 N/2 点的 FFT。
这样,通过将原问题不断分解为两个一半规模的子问题,然后计算相应的蝶形运算单元,最终得以完成整个 FFT。
算法步骤
本次实验中,一维 FFT 采用递归实现,且仅支持长度为 2 的整数幂的情况。
算法步骤如下:
- 检查图像的尺寸,如果不是 2 的整数幂则直接退出。
- 对图像的灰度值进行归一化。
- 对图像的每一行执行一维 FFT,并保存为中间结果。
- 对上一步结果中的每一列执行一维 FFT,返回变换结果。
- 将零频分量移到频谱中心,并求绝对值进行可视化。
- 对中心化后的结果进行对数变换,以改善视觉效果。





 本文介绍了如何使用Python手工实现二维离散傅里叶变换(DFT)和二维离散余弦变换(DCT),包括实验原理、算法步骤和主要代码。傅里叶变换用于获取图像的傅里叶频谱,而DCT因其计算速度快在图像处理中也广泛应用。FFT利用分治策略将复杂度降至O(nlogn),DCT则通过对DFT取实部加速计算。实验中,对图像进行归一化处理,通过递归实现一维FFT,再进行二维FFT和DCT,最后对结果进行可视化和对数变换。
本文介绍了如何使用Python手工实现二维离散傅里叶变换(DFT)和二维离散余弦变换(DCT),包括实验原理、算法步骤和主要代码。傅里叶变换用于获取图像的傅里叶频谱,而DCT因其计算速度快在图像处理中也广泛应用。FFT利用分治策略将复杂度降至O(nlogn),DCT则通过对DFT取实部加速计算。实验中,对图像进行归一化处理,通过递归实现一维FFT,再进行二维FFT和DCT,最后对结果进行可视化和对数变换。
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 1161
1161

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








