HDU 1506 Largest Rectangle in a Histogram(DP·单调栈)

题意  求条形图中最大矩形的面积  输入给你条的个数  每个条的高度hi   （以下等于也视为高）

只要知道第i个条左边连续多少个（a）比他高   右边连续多少个（b）比他高  那么以这个条为最大高度的面积就是hi*(a+b+1);

但是直接枚举每一个的话肯定会超时的   超时代码

#include<cstdio>
using namespace std;
const int N = 100005;
typedef long long ll;
ll h[N]; int n,wide[N];
int main()
{
    while (scanf ("%d", &n), n)
    {
        for (int i = 1; i <= n; ++i)
            scanf ("%I64d", &h[i]);
        for (int i = 1; i <= n; ++i)
        {
            wide[i] = 1;
            int k = i;
            while (k > 1 && h[--k] >= h[i]) ++wide[i];
            k = i;
            while (k < n && h[++k] >= h[i]) ++wide[i];
        }
        ll ans = 0;
        for (int i = 1; i <= n; ++i)
            if (h[i]*wide[i] > ans) ans = h[i] * wide[i];
        printf ("%I64d\n", ans);
    }
    return 0;
}

可以发现   当第i-1个比第i个高的时候   比第i-1个高的所有也一定比第i个高  

于是可以用到动态规划的思想

令left[i]表示包括i在内比i高的连续序列中最左边一个的下标  right[i]为最右边一个的下标

那么有   当 h[left[i]-1]>=h[i]]时   left[i]=left[left[i]-1] 从前往后可以递推出left[i]   

同理      当 h[right[i]+1]>=h[i]]时  right[i]=right[right[i]+1]从后往前可递推出righ[i]

最后答案就等于 max{(right[i]-left[i]+1)*h[i]}了

#include<cstdio>
using namespace std;
const int N = 100005;
typedef long long ll;
ll h[N];
int n, left[N], right[N];
int main()
{
    while (scanf ("%d", &n), n)
    {
        for (int i = 1; i <= n; ++i)
            scanf ("%I64d", &h[i]), left[i] = right[i] = i;


        h[0] = h[n + 1] = -1;
        for (int i = 1; i <= n; ++i)      //求left[i]
            while (h[left[i] - 1] >= h[i])
                left[i] = left[left[i] - 1];


        for (int i = n; i >= 1; --i)      //求right[i]
            while (h[right[i] + 1] >= h[i])
                right[i] = right[right[i] + 1];


        ll ans = 0;
        for (int i = 1; i <= n; ++i)
            if (h[i] * (right[i] - left[i] + 1) > ans) ans = h[i] * ll (right[i] - left[i] + 1);
        printf ("%I64d\n", ans);
    }
    return 0;
}

然后还有单调栈写法  比DP操作起来更容易  

通过单调栈可以在 O(n) 时间内找到数组中在 h[i] 左边(右边)离 h[i] 最近的大于 h[i] 那个数(或者下标)   这里是取下标   知道 h[i] 左边最近和右边最近的高度小于 h[i] 的两个下标后  那么就知道以这个矩形高度为基准的大矩形的面积了  

#include <cstdio>
#include <cstring>
using namespace std;
const int N = 1e5 + 5;
typedef long long ll;
ll h[N], s[N], le[N], ri[N];

int main()
{
    int n, top;
    while(scanf("%d", &n), n)
    {
        for(int i = 1; i <= n; ++i)
            scanf("%I64d", &h[i]);

        top = 0, s[0] = 0;   //le[i]保存i左边第一个小于h[i]的下标
        for(int i = 1; i <= n; ++i)
        {
            while(top && h[s[top]] >= h[i]) --top;
            le[i] = s[top];
            s[++top] = i;
        }

        top = 0, s[0] = n + 1;  //ri[i]保存i右边最后一个大于等于h[i]的下标
        for(int i = n; i > 0; --i)
        {
            while(top && h[s[top]] >= h[i]) --top;
            ri[i] = s[top] - 1;
            s[++top] = i;
        }

        ll ans = h[1];
        for(int i = 1; i <= n; ++i)
            if(h[i] * (ri[i] - le[i]) > ans)
                ans =  h[i] * (ri[i] - le[i]);
        printf("%I64d\n", ans);
    }
    return 0;
}

Largest Rectangle in a Histogram

Problem Description

A histogram is a polygon composed of a sequence of rectangles aligned at a common base line. The rectangles have equal widths but may have different heights. For example, the figure on the left shows the histogram that consists of rectangles with the heights 2, 1, 4, 5, 1, 3, 3, measured in units where 1 is the width of the rectangles:

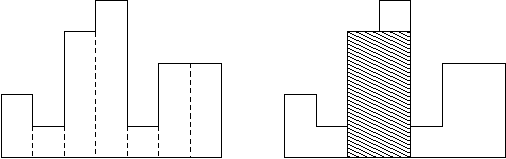
Usually, histograms are used to represent discrete distributions, e.g., the frequencies of characters in texts. Note that the order of the rectangles, i.e., their heights, is important. Calculate the area of the largest rectangle in a histogram that is aligned at the common base line, too. The figure on the right shows the largest aligned rectangle for the depicted histogram.

 

Input

The input contains several test cases. Each test case describes a histogram and starts with an integer n, denoting the number of rectangles it is composed of. You may assume that 1 <= n <= 100000. Then follow n integers h1, ..., hn, where 0 <= hi <= 1000000000. These numbers denote the heights of the rectangles of the histogram in left-to-right order. The width of each rectangle is 1. A zero follows the input for the last test case.

 

Output

For each test case output on a single line the area of the largest rectangle in the specified histogram. Remember that this rectangle must be aligned at the common base line.

 

Sample Input

7 2 1 4 5 1 3 3
4 1000 1000 1000 1000
0

 

Sample Output

8
4000