HDU6050-Funny Function

最新推荐文章于 2017-08-05 16:28:12 发布

a7f650ebd327889c

最新推荐文章于 2017-08-05 16:28:12 发布

阅读量207

点赞数

CC 4.0 BY-SA版权

分类专栏：数学，几何，积分矩阵快速幂文章标签：数学多校

本文链接：https://blog.youkuaiyun.com/a7f650ebd327889c/article/details/76243341

矩阵快速幂同时被 2 个专栏收录

16 篇文章

订阅专栏

数学，几何，积分

12 篇文章

订阅专栏

本文探讨了一种特定的递推关系及其解决方法，利用矩阵快速幂技术进行高效计算。通过对递推式的归纳和推导，作者展示了如何将复杂的递推问题转化为简单的矩阵运算，并给出了具体的C++代码实现。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

多校好难啊补题吧。。。。
看了题解发现有些东西不清楚啊。。。。

对于任意i>=1，当j>=3时，有通过归纳法可以得到

来推推吧：

1. 当 i=1时显然成立，

2. 假设当 i= k-1时成立

3. 当 i=k时

F i-1,j = F i-1,j-1 + 2*F i-1,j-2

= F i-1,j-1 + F i-1,j-2 + F i-1,j-3 + 2*F i-1,j-4

= F i-1,j-1 + F i-1,j-2 + F i-1,j-3 + ………… + 2* Fi-1,j-n (n为偶)

F i-1,j - Fi-1,j-n = F i-1,j-1 + F i-1,j-2 + F i-1,j-3 + ………… + Fi-1,j-n = F i,j-n

Fi,j-n = F i-1,j - Fi-1,j-n

Fi,j-n-1 = F i-1,j-1 - Fi-1,j-n-1

Fi,j-n-2 = F i-1,j-2 - Fi-1,j-n-2

因为 F i-1, j = F i-1,j-1 + 2 * F i-1,j-2

因为 Fi-1,j-n = Fi-1,j-n-1 + 2 * Fi-1,j-n-2

所以 Fi,j-n = Fi,j-n-1 + 2 * Fi,j-n-2

所以 Fi,j = Fi,j-1 + 2 * Fi,j-2

综上所述

(推导不是很严谨)

Fi,j＋１ = Fi,j + Fi,j-１＋…………＋２＊Ｆｉ，１　　　　　　　　　　　　　　（ｊ为偶）

Fi,j＋１ = Fi,j + Fi,j-１＋…………＋２＊Ｆｉ，２＋Ｆｉ，１－Ｆｉ，１　　　　（ｊ为奇）

同理我们易可以得到

接着这个就不必多解释了吧，

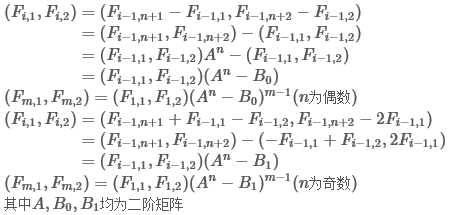
还是推推吧

#include<stdio.h>
#include<iostream>
#include<string.h>
using namespace std; 
#define N  1000000007
struct node
{
	long long a[2][2];
}; 
const node A={0,2,1,1};
const node B0={1,0,0,1};
const node B1={-1,2,1,0};
const node A0={1,1,0,0};
node cheng(node x,node y)
{
	node c;
	memset(c.a,0,sizeof(c.a));
	for(long long i=0;i<2;i++)
	for(long long j=0;j<2;j++)
	for(long long k=0;k<2;k++)
	c.a[i][j]=(c.a[i][j]+(x.a[i][k] * y.a[k][j])%N)%N;
	return c;
}
node jian(node x,node y)
{
	node c;
	c.a[0][0]=x.a[0][0]-y.a[0][0];
	c.a[0][1]=x.a[0][1]-y.a[0][1];
	c.a[1][0]=x.a[1][0]-y.a[1][0];
	c.a[1][1]=x.a[1][1]-y.a[1][1];
	return c;
}
node qc(node a,long long b)
{
	node c;
	c.a[0][0]=c.a[1][1]=1;c.a[0][1]=c.a[1][0]=0;
	while(b)
	{
		if(b&1)	c=cheng(c,a);		
		a=cheng(a,a);
		b>>=1;
	
	}
	return c;
}
int main()
{
	long long n,m;
	int t;
	scanf("%d",&t);
	while(t--)
	{
	    scanf("%lld%lld",&n,&m);
		node d=A;
		d=qc(d,n);
		if(n&1) d=jian(d,B1);
		else d=jian(d,B0);
		d=cheng(A0,qc(d,m-1));
		cout<<d.a[0][0]<<endl;
	}
	return 0; 
}

有这么个公式，不知道怎么推的，还在想，想到在补

F(m,1)=(2*k1^(m-1)+(1+(-1)^(m+1))/2)/3 其中k1=(2^n-1);