2017 ACM Arabella Collegiate Programming Contest Competitive Seagulls

Competitive Seagulls

time limit per test

1.0 s

memory limit per test

256 MB

input

standard input

output

standard output

There are two seagulls playing a very peculiar game. First they line up N unit squares in a line, all originally colored white.

Let L be the length of the longest continuous sub-segment of white unit squares. Let P be any prime that satisfies the condition that 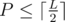. The player can choose any P if it satisfies the conditions but if there is no value of P that does, then P is set to 1.

The current player then proceeds to choose any continuous sub-segment of white unit squares of length P and paint them black. The player who can’t make a move loses.

If both players play optimally and the first player starts, which player is going to win the game?

Input

The first line of input is T – the number of test cases.

Each test case contains a line with a single integer N (1 ≤ N ≤ 107).

Output

For each test case, output on a single line "first" (without quotes) if the first player would win the game, or "second" if the second would win.

Example

input

2
2
5

output

second
first

题意：给你一个长度为n的方格，方格上面都被染色成了白色。每次染色都是选择白色的，假设目前选择的这块白色（白色联通块）的长度为L，每次都只能选择 <= (L + 1) / 2的素数染色。两个人轮流把这些方格染成黑色，把最后一格染黑的人获胜。问最后谁获胜

解题思路：这题其实和质数并没有关系。当n为偶数的时候，只需要先手取最中间两个，然后和后手对称取就能赢了，所以n>2且为偶数时，先手获胜。当n为奇数的时候，只需要先手取最中间三个，然后和对手对称取就能赢了，所以n>3且为奇数时，先手获胜。当n = 1时，先手获胜。当n = 2时，后手获胜。当n = 3时，后手获胜。

#include <iostream>  
#include <cstdio>  
#include <cstring>  
#include <string>  
#include <algorithm>  
#include <cmath>  
#include <map>  
#include <set>  
#include <stack>  
#include <queue>  
#include <vector>  
#include <bitset>  
#include <functional>  

using namespace std;

#define LL long long  
const int INF = 0x3f3f3f3f;

int main()
{
	int t, n;
	scanf("%d", &t);
	while (t--)
	{
		scanf("%d", &n);
		if (n == 2 || n == 3) printf("second\n");
		else printf("first\n");
	}
	return 0;
}