用Tensorflow搭建第一个神经网络

简述

https://blog.youkuaiyun.com/a19990412/article/details/82913189
根据上面链接中的前两个学习教程学习
其中Mofan大神的例子非常好，学到了很多
https://morvanzhou.github.io/tutorials/machine-learning/tensorflow/3-2-create-NN/

搭建这个神经网络

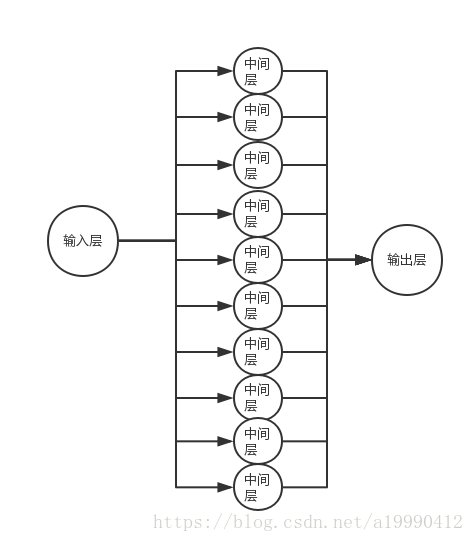
其实是从一个层到10层再到10层的这样的一个神经网络。（画图丑。。。求谅解。。就别私戳了）

解析

• 初始的输入的矩阵为：[[1],300个,[-1]] 大致这样的
• 在增加一层的那个函数中，最为经典的地方是，偏置（biases）的第一个维度必须选为1。看下面推理。
• 第一部分：
• 输入为：(300*1)的矩阵，之后，经过了第一个层，就是(300 * 1)* (1*10) + (1, 10)。这显然是合理的，每一层的数据，到神经网络中的中间层的每一个节点上，然后每个节点上都加一个偏置biases。

就是在每个上都同时加，通过下面的例子就可以看出来。

>>> import numpy as np
>>> a = np.random.normal(0, 1, (2, 4))
>>> a
array([[-0.60675395, -0.06779251,  1.50473051, -0.82511157],
       [ 1.14550373,  0.372316  ,  0.45110457, -0.41554109]])
>>> b = np.random.normal(0, 1, (1, 4))
>>> b
array([[ 0.48946834, -0.70514578,  2.12102107, -0.25960606]])
>>> a + b
array([[-0.11728561, -0.77293828,  3.62575157, -1.08471763],
       [ 1.63497208, -0.33282978,  2.57212564, -0.67514715]])
>>>

• 第二部分:
• 输出的内容为上面的输出：（300*10）的矩阵。
• 进行的计算为：(300 * 10) * (10 * 1) + (1, 1) 后面的那个为偏置，每个都加上了这样的一个偏置。

经过上面的推理，我们就可以理解了为什么中间添加新的一层的时候，需要将biases的第一次参数为1

• 发现写tensorflow就想当于写数学公式一样，怪不得TensorFlow在研究数学的老师那边那么容易上手 hhh

代码

import tensorflow as tf
import numpy as np

# TensorFlow嫌弃了我这台电脑的CPU(我这就避免了警报)
# ==================
import os

os.environ['TF_CPP_MIN_LOG_LEVEL'] = '2'
# ==================

# 创建一些等距离的数据(数据量为300)，同时用np.newaxis进行扩展一个维度
x_data = np.linspace(-1, 1, 300, dtype=np.float32)[:, np.newaxis]
# 创建同等规模的噪音(这里采用的是均值为0,标准差为0.05的,保持shape和类型一致)
noise = np.random.normal(0, 0.05, x_data.shape).astype(np.float32)
# 原数据label(y = x^2 - 0.5) 之后添加一点点噪声(让人感觉更像现实中获取的数据一样)
y_data = np.square(x_data) - 0.5 + noise


# 创建一个添加层数的函数,使得实现变得简单
# inputs是输出的东西，in_size表示的是该层的输入层维度，out_size表示的是该层的输出层维度，activation_function就是一个
def add_layer(inputs, in_size, out_size, activation_function=None):
    # 创建系数矩阵，矩阵规模为 [in_size * out_size]
    Weights = tf.Variable(tf.random_normal([in_size, out_size]))
    # 创建一个biases矩阵，这里考虑到biases用0不是那么好，所以，一开始设置的时候加个0.1
    biases = tf.Variable(tf.zeros([1, out_size]) + 0.1)
    # 构建方程
    Wx_plus_b = tf.matmul(inputs, Weights) + biases

    if activation_function == None:
        output = Wx_plus_b
    else:
        output = activation_function(Wx_plus_b)
    return output


xs = tf.placeholder(tf.float32, [None, 1])
ys = tf.placeholder(tf.float32, [None, 1])
# 得到中间那一层
l1 = add_layer(xs, 1, 10, activation_function=tf.nn.relu)
# 得到输出层
prediction = add_layer(l1, 10, 1)
# 在300个求一个平方和的均值，设置了切片的index为1，原因是最后的矩阵规模为300*1，大致类似:[[1],300个,[2]]
loss = tf.reduce_mean(tf.reduce_sum(tf.square(ys - prediction),
                                    reduction_indices=[1]))
# 梯度下降训练
train_step = tf.train.GradientDescentOptimizer(0.1).minimize(loss)
# 变量初始化
init = tf.global_variables_initializer()
# 启动会话
with tf.Session() as sess:
    sess.run(init)
    for i in range(1000):
        # training
        sess.run(train_step, feed_dict={xs: x_data, ys: y_data})
        if i % 50 == 0:
            # to see the step improvement
            print(sess.run(loss, feed_dict={xs: x_data, ys: y_data}))

附上有图形演示的代码

由于不同起始数据，画出几个不同的结果。下面列举其中的两个

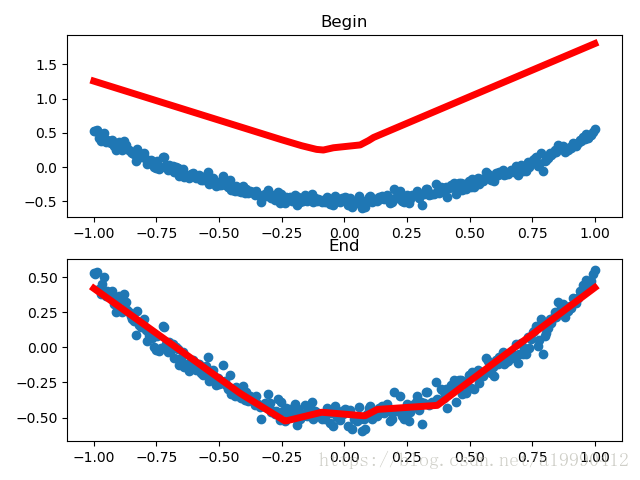
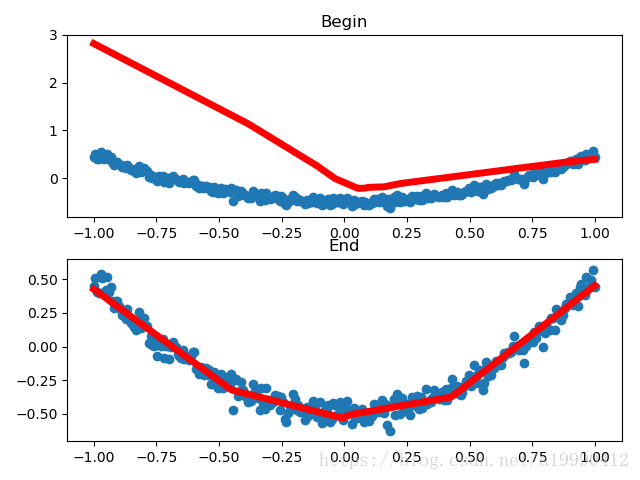
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
# TensorFlow嫌弃了我这台电脑的CPU(我这就避免了警报)
# ==================
import os

os.environ['TF_CPP_MIN_LOG_LEVEL'] = '2'
# ==================

# 创建一些等距离的数据(数据量为300)，同时用np.newaxis进行扩展一个维度
x_data = np.linspace(-1, 1, 300, dtype=np.float32)[:, np.newaxis]
# 创建同等规模的噪音(这里采用的是均值为0,标准差为0.05的,保持shape和类型一致)
noise = np.random.normal(0, 0.05, x_data.shape).astype(np.float32)
# 原数据label(y = x^2 - 0.5) 之后添加一点点噪声(让人感觉更像现实中获取的数据一样)
y_data = np.square(x_data) - 0.5 + noise


# 创建一个添加层数的函数,使得实现变得简单
# inputs是输出的东西，in_size表示的是该层的输入层维度，out_size表示的是该层的输出层维度，activation_function就是一个
def add_layer(inputs, in_size, out_size, activation_function=None):
    # 创建系数矩阵，矩阵规模为 [in_size * out_size]
    Weights = tf.Variable(tf.random_normal([in_size, out_size]))
    # 创建一个biases矩阵，这里考虑到biases用0不是那么好，所以，一开始设置的时候加个0.1
    biases = tf.Variable(tf.zeros([1, out_size]) + 0.1)
    # 构建方程
    Wx_plus_b = tf.matmul(inputs, Weights) + biases

    if activation_function == None:
        output = Wx_plus_b
    else:
        output = activation_function(Wx_plus_b)
    return output


xs = tf.placeholder(tf.float32, [None, 1])
ys = tf.placeholder(tf.float32, [None, 1])
# 得到中间那一层
l1 = add_layer(xs, 1, 10, activation_function=tf.nn.relu)
# 得到输出层
prediction = add_layer(l1, 10, 1)
# 在300个求一个平方和的均值，设置了切片的index为1，原因是最后的矩阵规模为300*1，大致类似:[[1],300个,[2]]
loss = tf.reduce_mean(tf.reduce_sum(tf.square(ys - prediction),
                                    reduction_indices=[1]))
# 梯度下降训练
train_step = tf.train.GradientDescentOptimizer(0.1).minimize(loss)
# 变量初始化
init = tf.global_variables_initializer()
# 启动会话
with tf.Session() as sess:
    sess.run(init)
    fig = plt.figure()
    # 创建两个子图
    ax_begin = fig.add_subplot(2, 1, 1)
    ax_end = fig.add_subplot(2, 1, 2)
    ax_begin.scatter(x_data, y_data)
    ax_end.scatter(x_data, y_data)

    # 起始版
    prediction_value = sess.run(prediction, feed_dict={xs: x_data})
    # plot the prediction
    ax_begin.plot(x_data, prediction_value, 'r-', lw=5)
    ax_begin.set_title("Begin")
    plt.tight_layout()

    for i in range(1000):
        # training
        sess.run(train_step, feed_dict={xs: x_data, ys: y_data})
        if i % 50 == 0:
            # to see the step improvement
            print(sess.run(loss, feed_dict={xs: x_data, ys: y_data}))

    # 经过迭代后的版本
    prediction_value = sess.run(prediction, feed_dict={xs: x_data})
    # plot the prediction
    ax_end.plot(x_data, prediction_value, 'r-', lw=5)
    ax_end.set_title("End")
    plt.show()