K-means

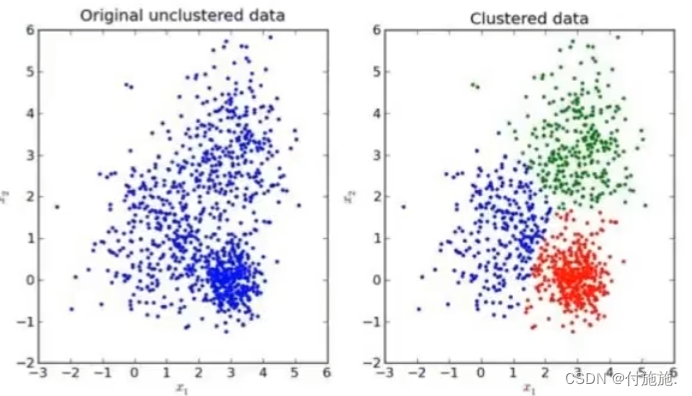
先来看一下一个K-means的聚类效果图

在 K-Means 算法中，距离最近通常是指欧几里得距离（Euclidean distance）。欧几里得距离是指两个数据点在特征空间内的直线距离。公式如下所示：

$distance(x_i,c_j)=\sqrt{{\sum }_{k=1}^d(x_{ik}-c_{jk}{)}^2}$

其中，$x_i$ 是数据集中的第 i 个数据点，$c_j$ 是聚类中心点，$d$ 是特征空间的维度数。通过计算数据点与各个聚类中心点之间的欧几里得距离，可以确定每个数据点所属的簇。

具体而言，在下面算法的第二步中，对于每个数据点 $x_i$，计算它与 K 个聚类中心点之间的距离（即 $distance(x_i,c_j)$），然后将其分配给距离最近的聚类中心点 $c_j$ 所代表的聚类。

简单来说，就是找到每个数据点与各个聚类中心点之间的欧几里得距离，然后将其归类到距离最近的聚类中心点所代表的聚类中去。

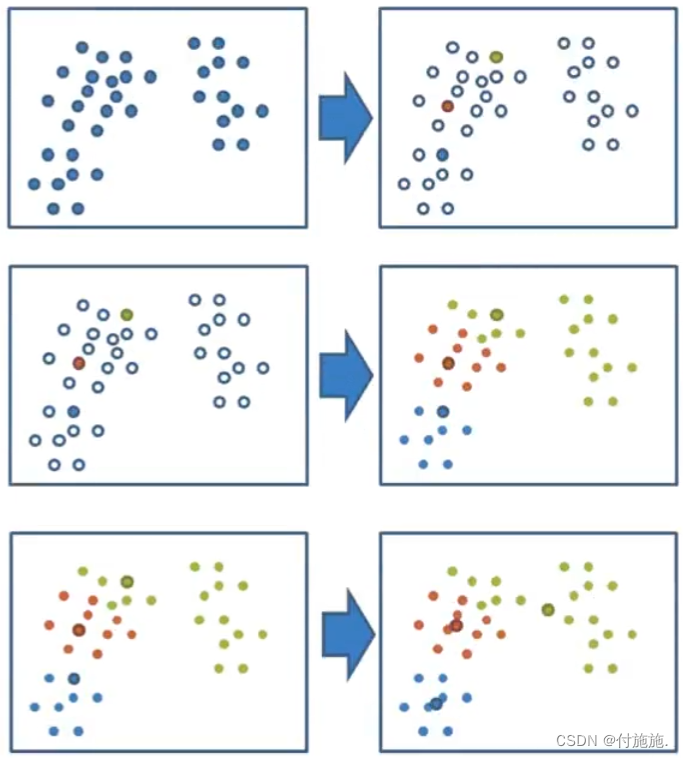
K-means聚类步骤

• 1、随机设置K个特征空间内的点作为初始的聚类中心（一开始就要设置）
• 2、对于其他的每个数据点，计算其到 K 个聚类中心的距离，并将其归类到距离最近的聚类中心所属的聚类。
• 3、对于每个聚类，重新计算其新的聚类中心，通常是使用该聚类所有数据点的平均值作为新的聚类中心。
• 4、如果新的聚类中心点与原来的聚类中心点相同，则结束算法；否则重复步骤 2 和 3，直到收敛为止。