1050 螺旋矩阵 C++

最新推荐文章于 2025-06-18 11:39:38 发布

原创最新推荐文章于 2025-06-18 11:39:38 发布 · 1.7k 阅读

6 ·

CC 4.0 BY-SA版权

文章标签：

#1050 螺旋矩阵 C++ #PAT

PAT甲级题目专栏收录该内容

100 篇文章

订阅专栏

本文介绍了一种生成螺旋矩阵的算法，通过使用二维数组和自定义排序，实现了元素按顺时针螺旋顺序填充矩阵。文章详细解释了算法思路，包括如何划分矩阵为多个小整体并分别处理，最终输出螺旋矩阵。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

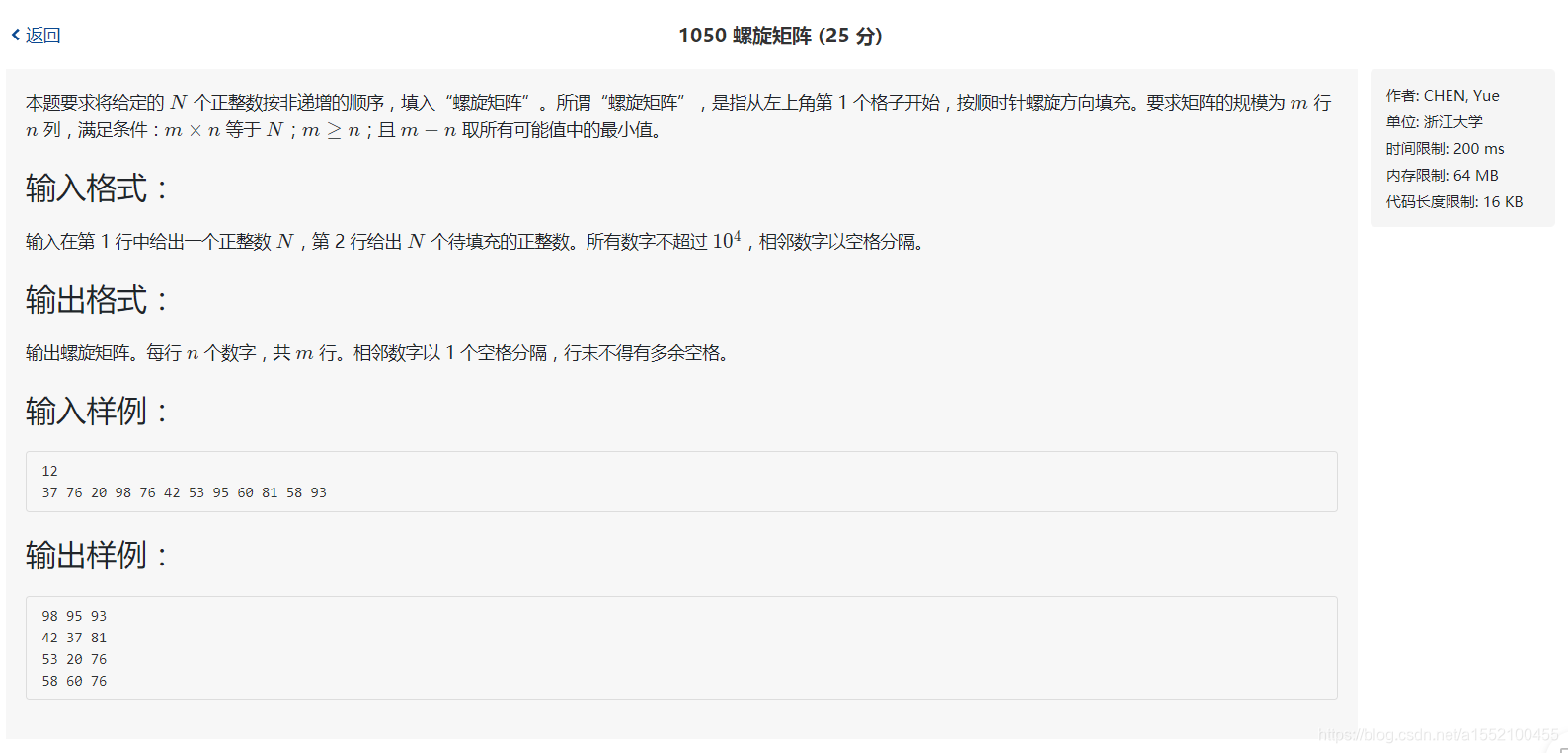
在这里插入图片描述
思路分析：
由于涉及到矩阵问题，使用二维数组比较方便。
将每一层矩阵（顺时针一圈为一层）看做一个小整体，整个矩阵是由若干个小整体从外向内一圈圈包围起来的。每个小整体又可看做由四小部分组成的，分别是上、右、下、左四部分。设法先找到每一小部分直接相连部分的次序关系，再循环执行小整体代码便可得到所求的螺旋矩阵。

为了方便找到连接点之间的规律，我们直接以角标排序。
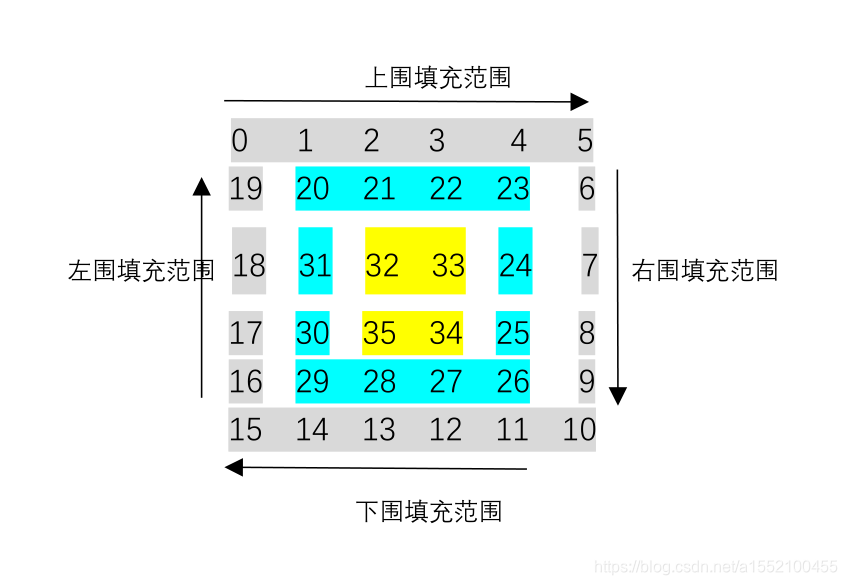
在这里插入图片描述
具体步骤：

创建一个二维数组gra用来存储螺旋矩阵中的元素，一个lib数组作为元素库，存放给出的元素。
计算m和n的值，并将lib数组降序排列；
执行m/2 + m%2次大循环，每个大循环里面包含四次小循环，并将元素储存到gra中；
输出结果。

示例代码：

#include<iostream>
#include<vector>
#include<algorithm>
#include<math.h>
using namespace std;
class Mysort{//自定义排序
public:
	bool operator()(const int m, const int n){
		return m > n;
	}
};
int main(){
	int num; cin>>num;
	int n,m;
	vector<int> lib(num);//作为元素库
	for(int i = 0; i < num; i++){
		int temp; cin>>temp;
		lib[i] = temp;
	}
	for(n = (int)sqrt((double)num); n >= 1; n--){
		if(num%n == 0){
			m = num/n;
			break;
		}
	}
	sort(lib.begin(),lib.end(),Mysort());//降序排列
	int t = 0;//指向lib数组
	vector<vector<int>> gra(m,vector<int> (n));//利用vector创建二维数组
	for(int i = 0; i < m/2 + m%2; i++){//循环轮数
		for(int j = i; j <= n-1-i && t < num; j++){//上围
			gra[i][j] = lib[t++];
		}
		for(int k = i+1; k <= m-1-i && t < num; k++){//右围
			gra[k][n-1-i] = lib[t++];
		}
		for(int k = n-2-i; k >= i && t < num; k--){//下围
			gra[m-1-i][k] = lib[t++];
		}
		for(int k = m-2-i; k >= i+1 && t < num; k--){//左围
			gra[k][i] = lib[t++];
		}
	}	
	for(int i = 0; i < m; i++){//输出
		for(int j = 0; j < n-1; j++){
			cout<<gra[i][j]<<" ";
		}
		cout<<gra[i][n-1]<<endl;
	}
	return 0;

}