1049 数列的片段和 C++

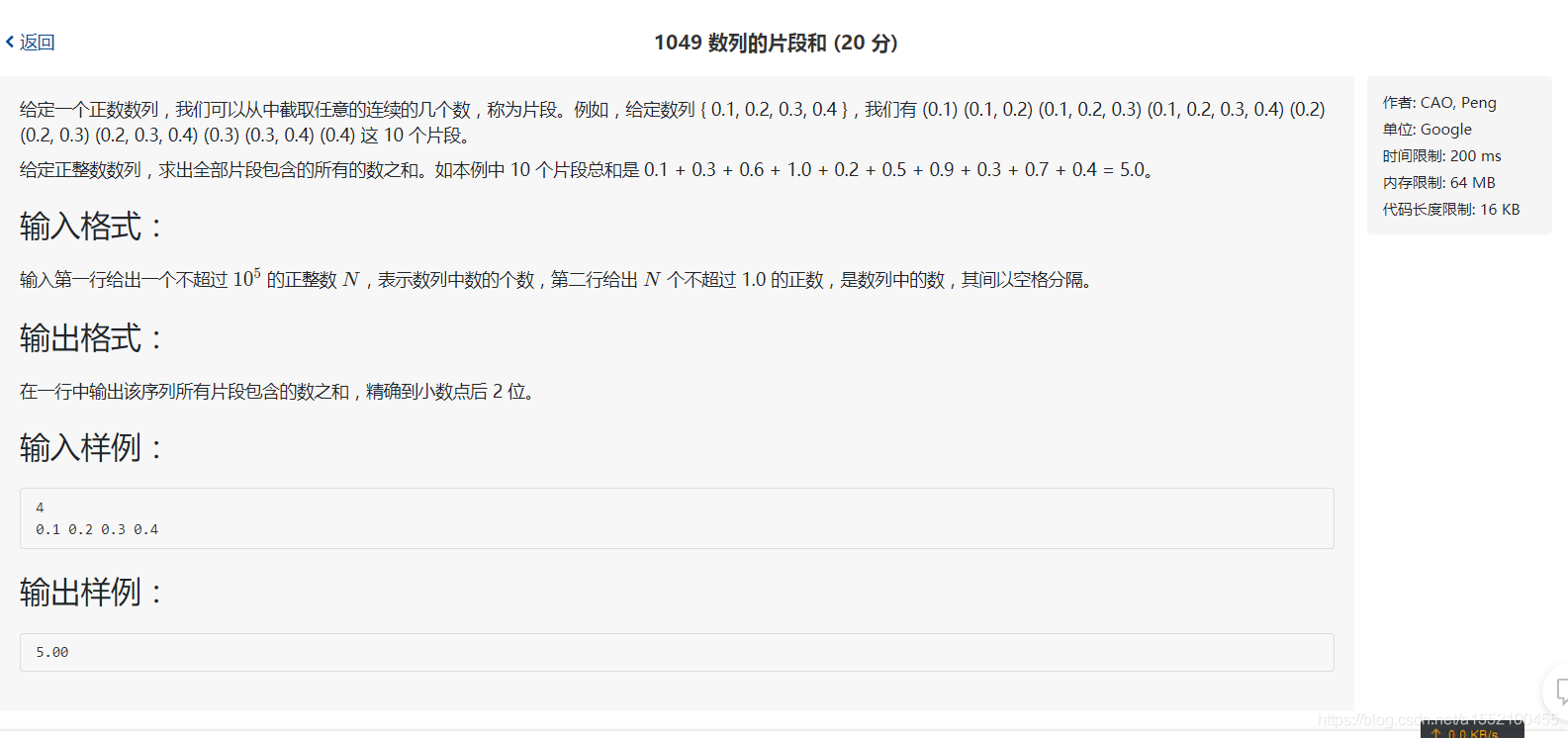
思路解析：
由于本题是统计所有片段和，所以从整体比从局部分析更便捷。
片段和等于各元素在各片段里出现次数与它本身之积的和。

设第i个数为要统计的元素为a，则以a为尾的片段共有i种，即：1 2…i、2 3…i、3 4…i、i，以a为头的片段共有n-i+1种，即：i i+1…n、i+1 i+2…n、n。
所有包含元素a的片段共有i*(n-i+1)种。所以所有元素a的和为ai(n-i+1)。

另外值得注意的是，对于混合类型的数据运算，最好要手动统一为同一类型，例如本题，a* i (n-i+1)和i(n-i+1)a的运算结果是不同的，前者的精度更高。如果要将后者的精度提升必须手动的将前部分转换为double类型，即（double）i(n-i+1)*a

示例代码：

#include<iostream>
#include<iomanip>
using namespace std;
int main() {
	int num; cin >> num;
	double res=0;
	for (int i = 1; i <= num; i++) {
		double temp; cin >> temp;
		res += temp*(num - i + 1)*i;
	}
	cout <<fixed<<setprecision(2)<<res;
	return 0;
}