1. 验证SO(3)、SE(3)和Sim(3)关于乘法成群。

2. 验证(R³,R,×)构成李代数。
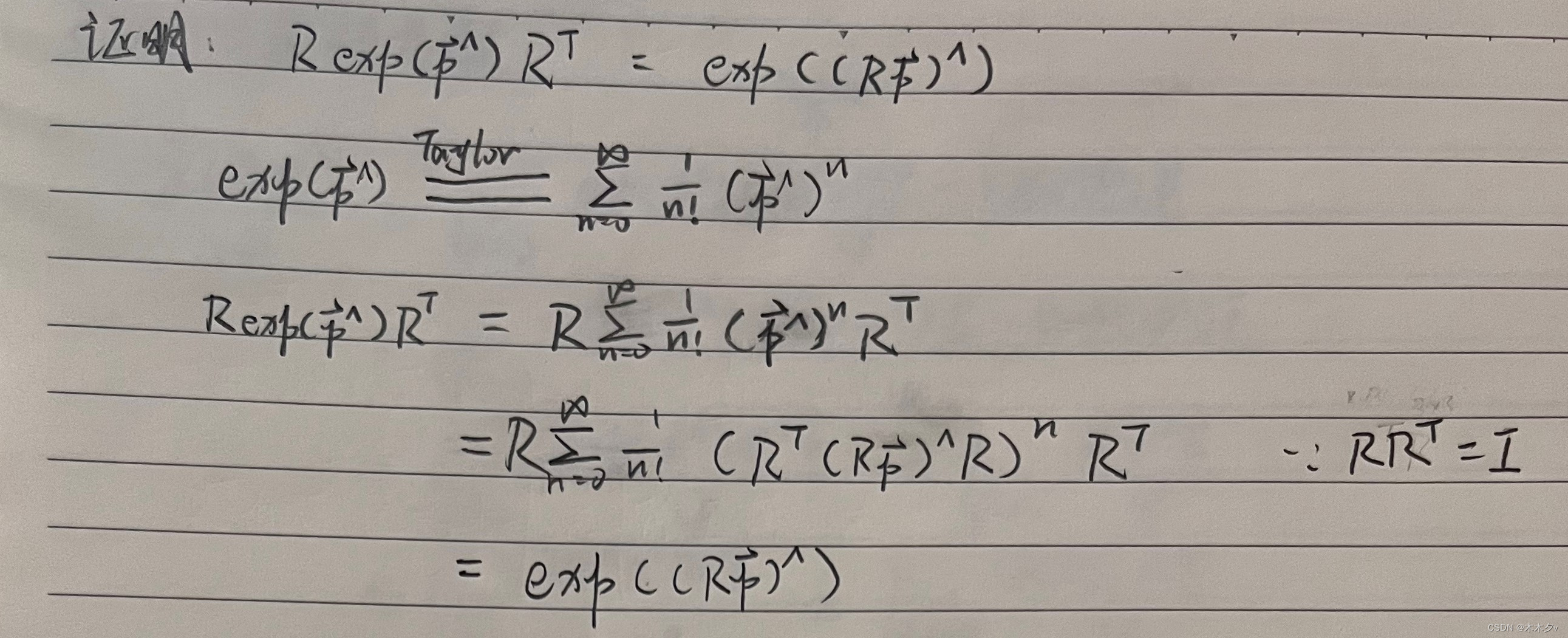

3. 验证so(3)和se(3)满足李代数要求的性质。

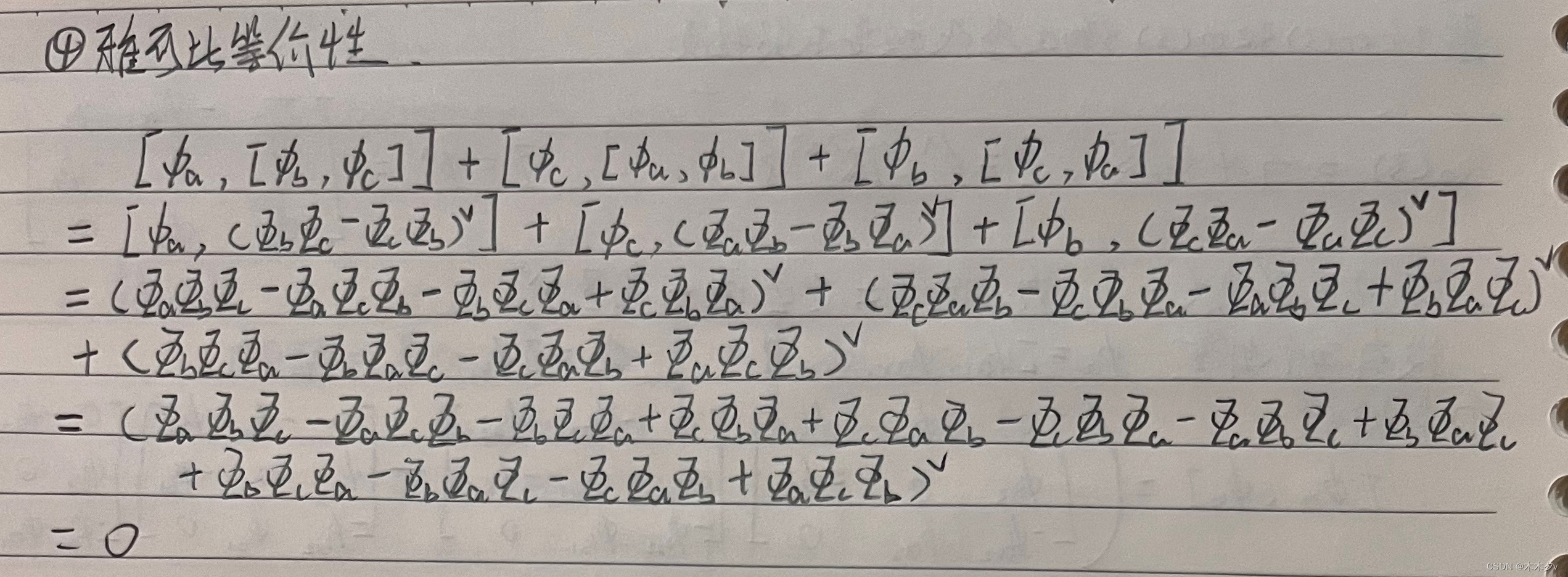
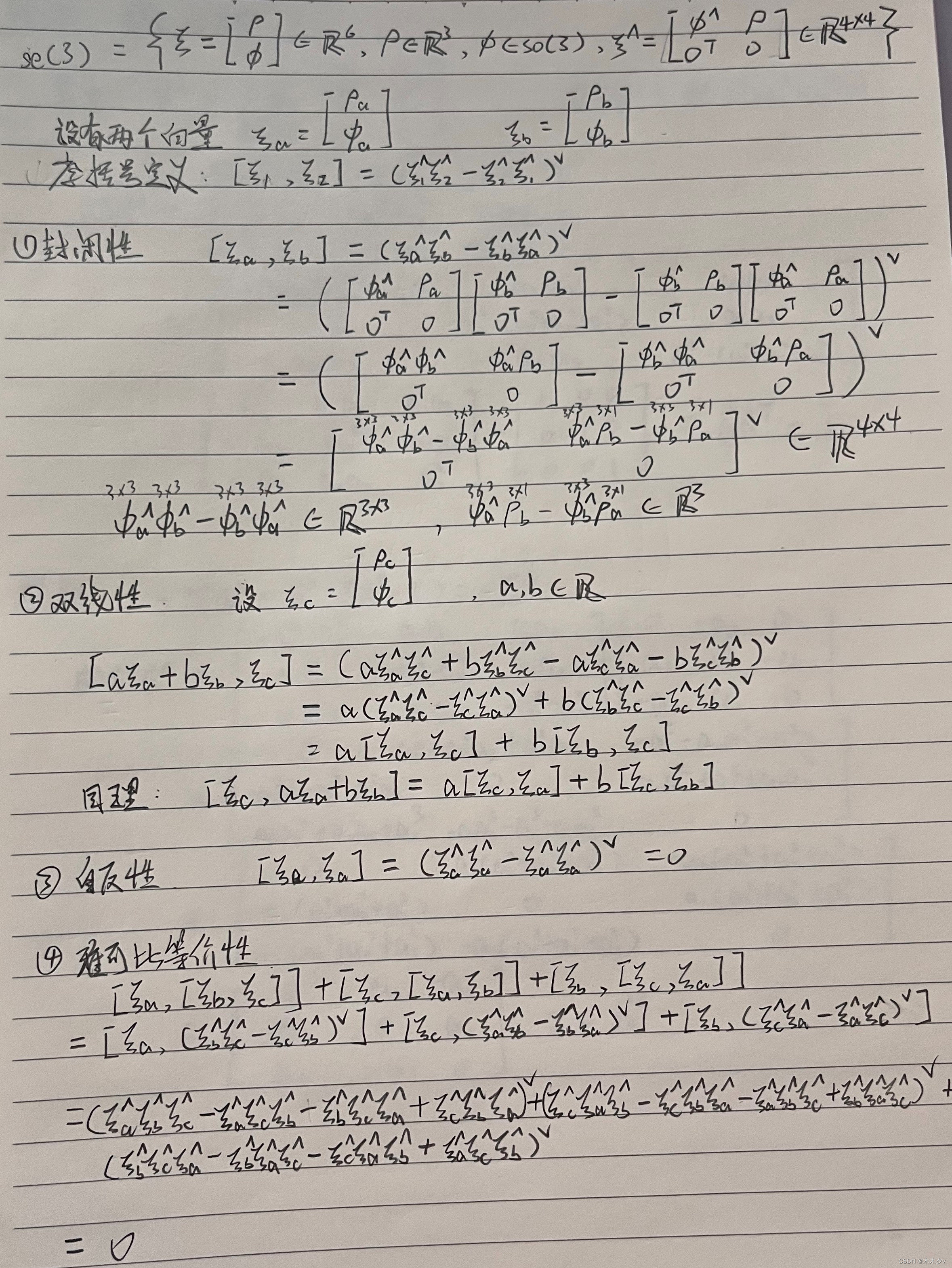
 本文探讨了数学中的群论概念,包括SO(3)、SE(3)和Sim(3)的乘法群性质验证,以及(R³,R,×)构成的李代数。同时,深入研究了李代数so(3)和se(3)的特性,并验证了相关性质。此外,文章还涉及了SO(3)和SE(3)的伴随性质及其在右扰动下的导数计算。最后,介绍了cmake和find_package指令在软件构建过程中的作用及其参数配置。
本文探讨了数学中的群论概念,包括SO(3)、SE(3)和Sim(3)的乘法群性质验证,以及(R³,R,×)构成的李代数。同时,深入研究了李代数so(3)和se(3)的特性,并验证了相关性质。此外,文章还涉及了SO(3)和SE(3)的伴随性质及其在右扰动下的导数计算。最后,介绍了cmake和find_package指令在软件构建过程中的作用及其参数配置。

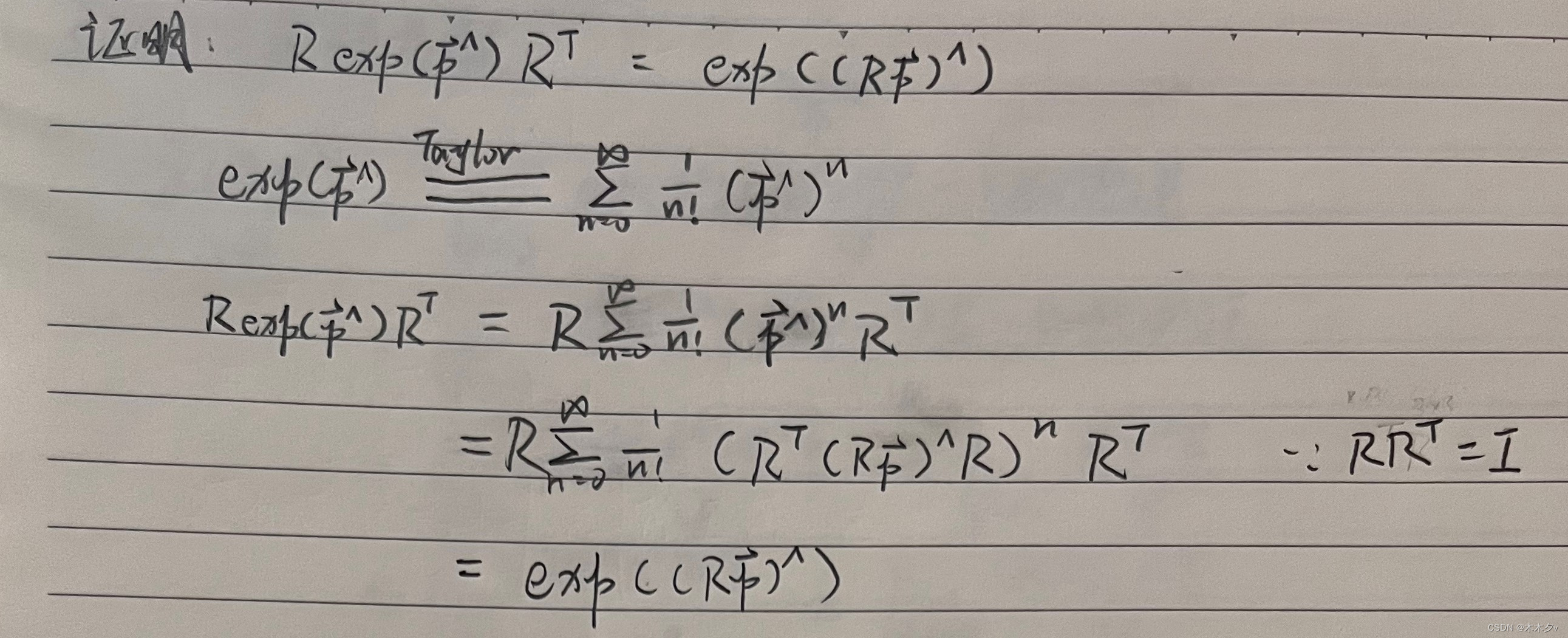


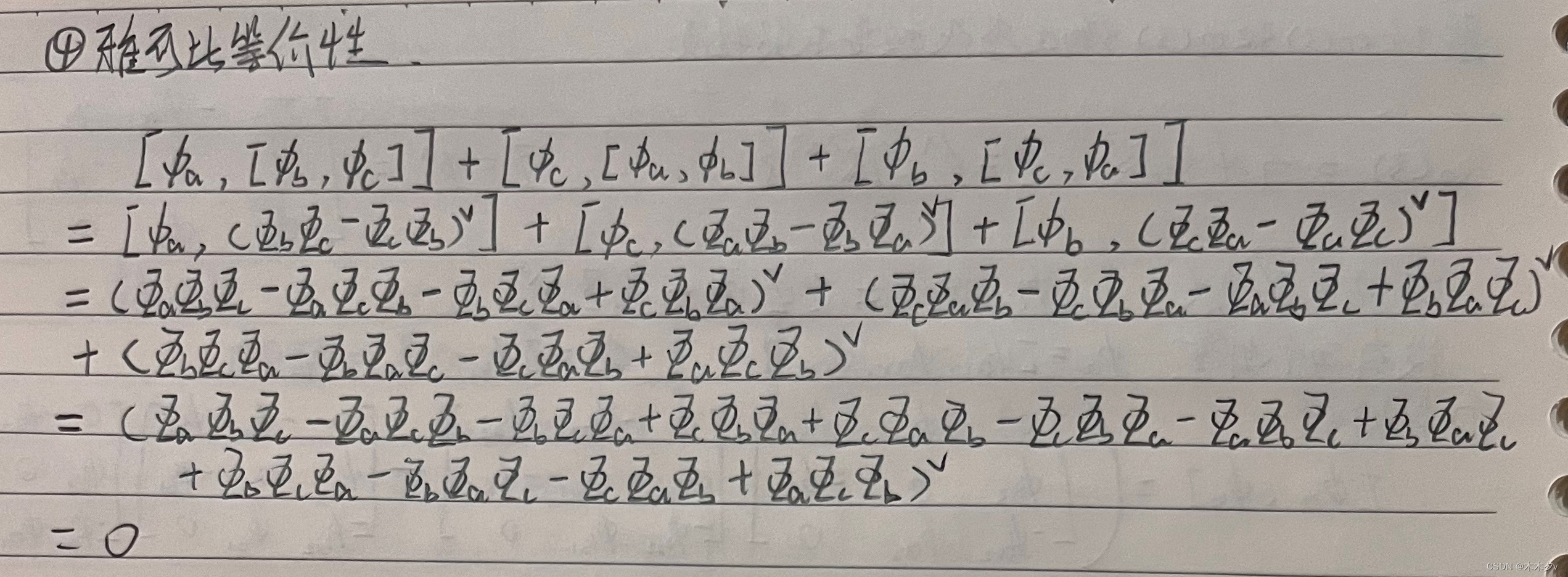
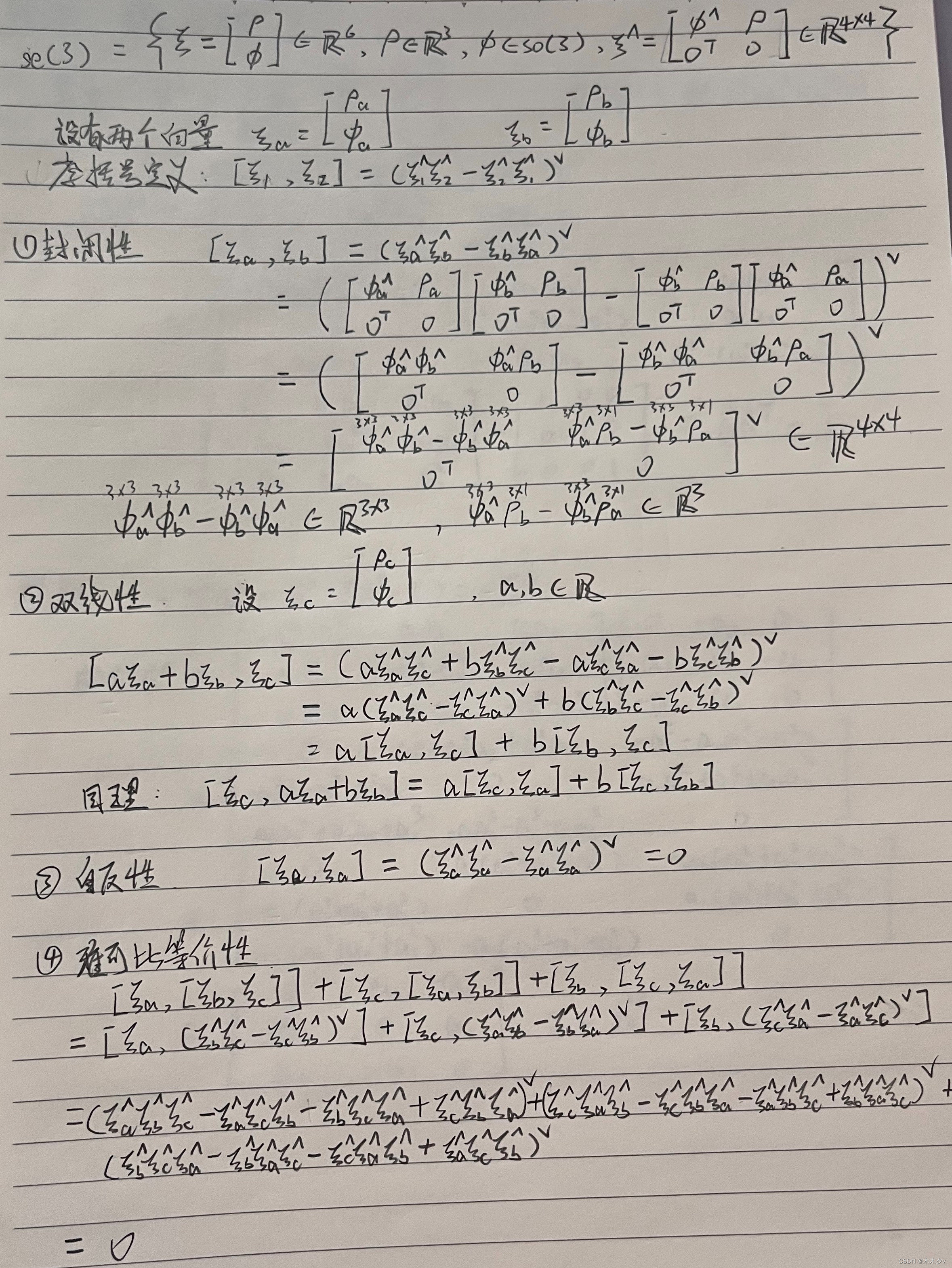
 766
766
 4471
4471
 875
875

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?


