点估计和区间估计
点估计
矩估计法
正态分布是一种统计量,目的是描述总体的某一性质。而矩则是描述这些样本值的分布情况,无论几阶矩,无外乎是描述整体的疏密情况。K阶矩分为原点矩和中心矩:
前者是绝对的:1阶就是平均值;2阶则是平方的平均值;3阶是立方的平均值,如此类推。
后者是相对于平均值而言:1阶即期望;2阶即方差的估计;如此类推。
原点矩
μk′=E(Yk){μ}'_{k}=E(Y^k)μk′=E(Yk) (k=1,2,…)
中心矩
μk=E[(Y−μ)k]μ_k=E[(Y-μ)^k]μk=E[(Y−μ)k]
k表示阶数
原点矩方法
对于总体:原点矩-E(Yk)E(Y^k)E(Yk)
对于样本:mk=∑i=1nyiknm_k=\frac{\sum_{i=1}^{n}y_{i}^{k}}{n}mk=n∑i=1nyik
Y:观测值
举例:
y1,y2,y3,...yny_1,y_2,y_3,...y_ny1,y2,y3,...yn代表一个随机样本的n个观测值,随机变量Y代表总体的分布,随机变量Y中有θ1,θ2,θ3,...θkθ_1,θ_2,θ_3,...θ_kθ1,θ2,θ3,...θkk个参数,矩估计需要估计出k个参数θ^1,θ^2,θ^3,...θ^k\hat{θ}_1,\hat{θ}_2,\hat{θ}_3,...\hat{θ}_kθ^1,θ^2,θ^3,...θ^k
θ^\hat{θ}θ^:E(Y)=1n∑yiE(Y)=\frac{1}{n}\sum y_iE(Y)=n1∑yi
θ^2\hat{θ}_2θ^2:E(Y2)=1n∑yi2E(Y^2)=\frac{1}{n}\sum {y_i}^2E(Y2)=n1∑yi2
一个参数使用一个方程,若K个参数则使用K个方程。求总体的平均值只有一个参数,使用一个方程就可。
假设:总体的期望为μ
则有E(Y)=μ
假设只有一个参数
此时使用矩估计的方法,只有一个参数,即使用一个方程:
Y的一阶原点矩μ1′=E(Y1){μ}'_{1}=E(Y^1)μ1′=E(Y1)既他的期望本身μ1′=E(Y1){μ}'_{1}=E(Y^1)μ1′=E(Y1)=μ
样本的一阶原点矩,既样本求和:μ=1n∑yiμ=\frac{1}{n}\sum y_iμ=n1∑yi这时发现公式似乎很眼熟:
xˉ=1n∑yi\bar{x}=\frac{1}{n}\sum y_ixˉ=n1∑yi
平均值不就是这么来的么。
当有两个参数时呢
可以设置第二个参数E(Y2)=1n∑yi2E(Y^2)=\frac{1}{n}\sum {y_i}^2E(Y2)=n1∑yi2
然后结合第一个式子用两个方程求解。
中心矩方法
其他参考上文
对于样本公式: ∑(yi−yˉ)kn\frac{\sum (y_i-\bar{y})^k}{n}n∑(yi−yˉ)k
其他方法
最大似然法/极大似然法,最小二乘法,刀切法,稳健估计,Bayes方法
区间估计
区间估计是一个区间,区间分别由Lower和Upper构成–>(Lower,Upper)称为置信区间,其中包含着被估计参数的概率称为置信水平/置信系数[概率]
如置信水平为95%,那么这个区间也叫95%置信区间。
虚轴法
假设有一个估计量θ^\hat{θ}θ^,E(θ^)E(\hat{θ})E(θ^)=θ,即θ^\hat{θ}θ^的期望=θ,θ为要估计的参数。
Z=θ^−θσθ^Z=\frac{\hat{θ}-θ}{\sigma _{\hat{θ}}}Z=σθ^θ^−θ
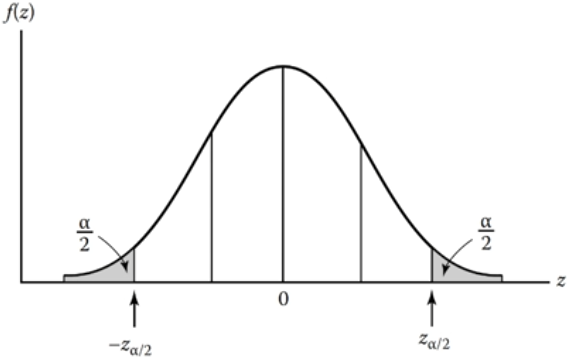
假设Z符合正态分布,整个正态分布图的面积为1,
阴影部分的面积为0.05,非阴影部分的面积则为1-0.05=0.95
可以将面接还原成概率,整体的概率为100%,那么Z落在非阴影区域的概率便为95%。
Z–>(−Zα/2-Z_{\alpha/2}−Zα/2,Zα/2Z_{\alpha/2}Zα/2)即(−Zα/2-Z_{\alpha/2}−Zα/2≤Z≤Zα/2Z_{\alpha/2}Zα/2)
在分布中,阴影部分的面积为α,空白区域即为1-α,分布的两翼阴影面积各为α/2,所以有Z=1-α:可推出如下公式。
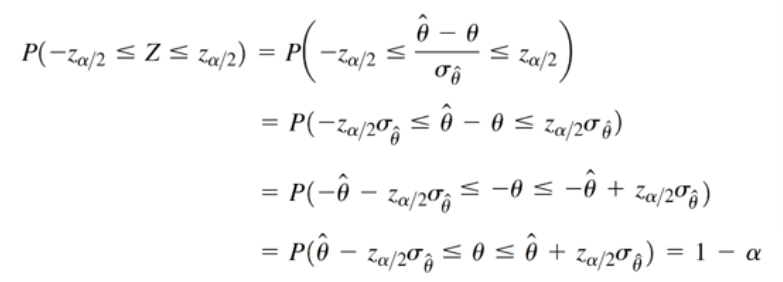
LCL=θ^−zα2σθ^\hat{θ}-z\frac{\alpha}{2}\sigma _{\hat{θ}}θ^−z2ασθ^ UCL=θ^+zα2σθ^\hat{θ}+z\frac{\alpha}{2}\sigma _{\hat{θ}}θ^+z2ασθ^
所以确定了如下步骤:
- 确定统计量θ
- 确定概率分布(利用概率密度函数)
- 求置信区间
同理,如果是卡方分布,t分布也可以依照相同的理论求值。







 本文详细介绍了点估计与区间估计在统计学中的应用。点估计通过矩估计法和最大似然法等方法确定总体参数的估计值,而区间估计则提供了一个置信区间来估计参数可能的范围。矩估计法中,原点矩和中心矩用于建立方程组求解参数,最大似然法则基于样本数据找到最可能的参数值。对于区间估计,通过标准误差和置信水平确定置信区间,常用Z、t或卡方分布进行计算。
本文详细介绍了点估计与区间估计在统计学中的应用。点估计通过矩估计法和最大似然法等方法确定总体参数的估计值,而区间估计则提供了一个置信区间来估计参数可能的范围。矩估计法中,原点矩和中心矩用于建立方程组求解参数,最大似然法则基于样本数据找到最可能的参数值。对于区间估计,通过标准误差和置信水平确定置信区间,常用Z、t或卡方分布进行计算。
















 1855
1855

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








