2022.03.07地毯

最新推荐文章于 2025-12-16 14:17:05 发布

原创最新推荐文章于 2025-12-16 14:17:05 发布 · 182 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #java #蓝桥杯

博客内容讲述了如何使用差分前缀和的方法解决二维数组区间加法问题，避免了暴力求解导致的时间超限错误。通过将二维数组转换为多个一维序列，逐行进行前缀和计算，实现了高效地更新和查询操作。

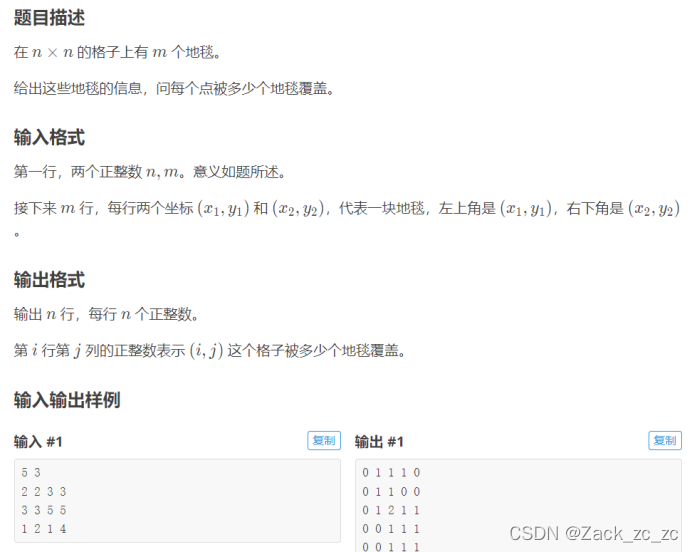
在这里插入图片描述

思路：

如果直接暴力，会出现TLE。这里采用差分-前缀的思想。

如果再一维序列中，要将某个区间[i, j]加1，只需要在第i位标1，第j+1位标-1，求前缀和即可。如下例：
在这里插入图片描述
所以，当在二维中，可以将二维看成很多一维序列组成，标记如下：

当把所有地毯都标记后，直接求出前缀和，即得解。

代码

	int n,m;
	int[][] ind;
	int[][] res;
	void test() throws IOException {
		Reader cin = new Reader();
		n = cin.nextInt();
		m = cin.nextInt();
		ind = new int[m][4];
		res = new int[n+1][n+1];
		for(int i = 0; i < m ;i++) {
			int x1 = cin.nextInt()-1;
			int y1 = cin.nextInt()-1;
			int x2 = cin.nextInt()-1;
			int y2 = cin.nextInt()-1;
			for(int k = x1; k <= x2; k++) {
				res[k][y1]++;
				res[k][y2+1]--;
			}
		}
		
		for(int i = 0; i < n; i++) {
			int s = 0;
			for(int j = 0; j < n; j++) {
				s+=res[i][j];
				res[i][j] = s;
				System.out.print(res[i][j]+" ");
			}
			System.out.println();
		}
	}