二叉搜索树相关

定义：

二叉搜索树又称二叉排序树，它或者是一棵空树，或者是具有以下性质的二叉树:若它的左子树不为空，则左子树上所有节点的值都小于根节点的值。 若它的右子树不为空，则右子树上所有节点的值都大于根节点的值。 它的左右子树也分别为二叉搜索树

对二叉搜索树的一些操作

基本结构

首先，我们先定义出一些结构
第一个结构是树里面的内容，包含左指针右指针，以及key和value。
接下来的一个类，用来表示这是一个二叉搜索树

template<class K, class V>
struct BSTreeNode
{
	BSTreeNode<K, V>* _left;
	BSTreeNode<K, V>* _right;
	K _key;
	V _value;

	BSTreeNode(const K& key, const V& value)
		:_left(nullptr)
		,_right(nullptr)
		,_key(key)
		,_value(value)
	{}
};

template<class K, class V>
class BSTree
{
	typedef BSTreeNode<K, V> Node;
public:
		Node* _root = nullptr;
};

Insert操作

Insert的思路是通过key去查找，看在树里面有没有这个节点，如果有就插入失败(因为二叉搜索树中不允许有重复的值出现，否则就失去了意义)。 如果没有那就去找一个合适的位置插入。
找合适的位置：①如果根为空，直接创建新节点当根节点插入 ②根不为空，就去子树上找。 这里我们要注意为了方便控制我们的循环条件，我们大循环是以cur为循环条件去找的，所以我们需要有parent来记录cur的父亲位置，这样后面才方便插入。（为什么不直接改循环条件？ 因为这里判断不仅仅是一个节点，它既需要判断左节点又要判断右节点，所以我们选择以parent的形式去记录）

bool Insert(const K& key, const V& value)
{
	// 1.根为空，直接插入一个新节点
	if (_root == nullptr)
	{
		_root = new Node(key, value);
		return true;
	}
	// 2.根不为空，则去找到合适位置插入
	Node* parent = _root;
	Node* cur = _root;
	while (cur)
	{
		if (cur->_key < key)
		{
			parent = cur;
			cur = cur->_right;
		}
		else if (cur->_key > key)
		{
			parent = cur;
			cur = cur->_left;
		}
		else return false;   // 如果找到相同的值那么插入失败了
	}
	// 此时，走出循环说明已经找到了插入位置，但此刻的cur已经是空指针了，我们应该需要的是cur的parent位置，所以上面需要有parent来记录
	cur = new Node(key, value);   // 直接重新赋值cur就可以了，不用再加一个新的变量进来
	if (key > parent->_key)
		parent->_right = cur;
	if (key < parent->_key)
		parent->_left = cur;
	return true;
}

Find操作

Find操作非常简单，找根，左孩子右孩子，如果遍历完了依然没有找到，那就返回空指针。

	Node* Find(const K& key)
	{
		Node* cur = _root;
		while (cur)
		{
			if (cur->_key > key)
				cur = cur->_left;
			else if (cur->_key < key)
				cur = cur->_right;
			else return cur;
		}
		return nullptr;
	}

Erase操作

Erase操作相对就会比较的麻烦了。
Erase的思路：首先，我们需要去判断这个节点是否存在，不存在返回false。存在才会有下面的删除操作(不存在的情况放在最外面了)。
删除节点分为三个情况：①删除的节点只有左孩子
②删除节点只有右孩子(没有孩子包含在这两种情况)
③既有左孩子又有右孩子
那么针对三种情况，我们有不同的要求，建议通过图形来进行理解：
①、②种是类似的。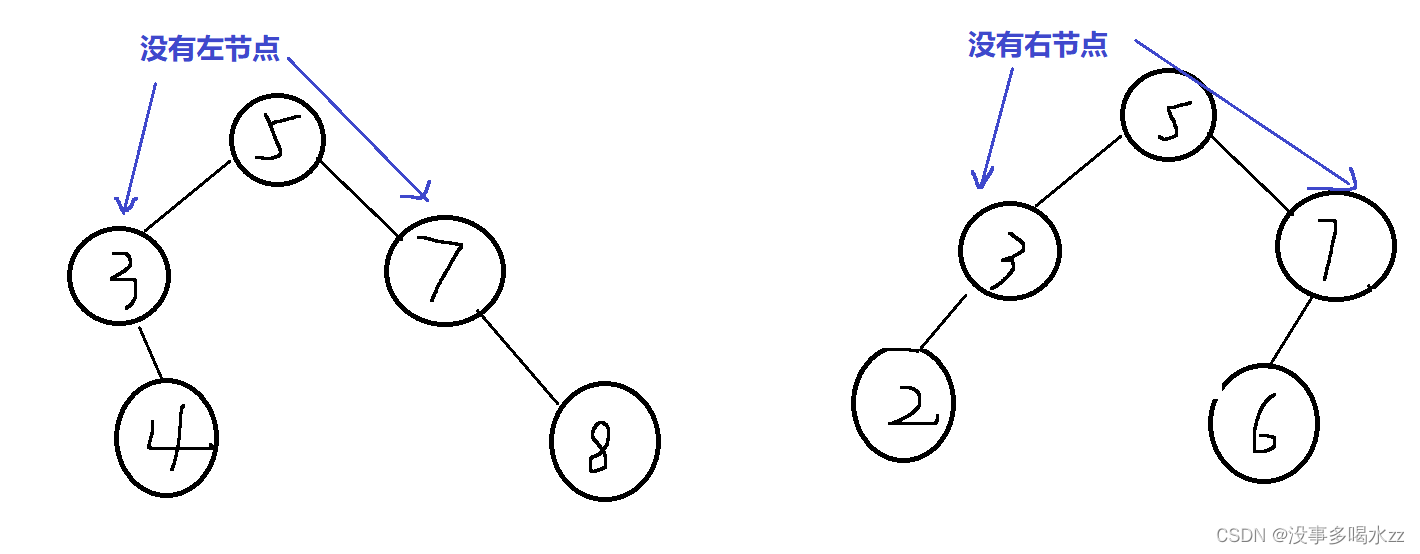
我们进行判断又分三种情况，第一种：我们要删除的节点就是根节点，那么就直接对根进行处理(我们说了删除节点无左右孩子也包含在①、②的情况里，这里就体现出来了，这里也可以处理)。 第二种：我们要删除的节点cur是parent的左孩子 第三种： 我们要删除的节点cur是parent的右孩子。 第二种和第三种情况是不一样的，这里结合图片就可以看出来。

难处理的是第③种情况
如果说我们删除的节点既有左孩子又有右孩子，那么在处理的时候需要用到交换法。 交换的对象是cur和cur左孩子中的最大值或右孩子中的最小值。
所以第一步是找到最大的左孩子或最小的右孩子(这里我们以找到最小右孩子为例)
找到之后，还要分情况讨论： 一种是这个最小的右孩子有左节点也有右节点的情况
还一种是这个最小的右孩子只有右节点的情况（注意：这里不可能出现这个节点还有左节点的情况，因为在此之前我们找到的这个RightMin是右子树的最小节点，就不可能出现它还有比他小的左节点的情况）
第二种可以看到，我们的RightMin还有一个右节点的情况，这个情况就得特殊处理了，如果RightMinParent->left = RightMin。我们RightMinParent的左节点就得指向RightMin的右结点(同样，RightMin不会有左节点)
这里我们怎么样更好的理解记忆呢？
我们可以看第一种情况是RightMinParent和RightMin二者成一条线。 第二种情况是不成一条线，RightMin为RightMinParent左孩子的情况。

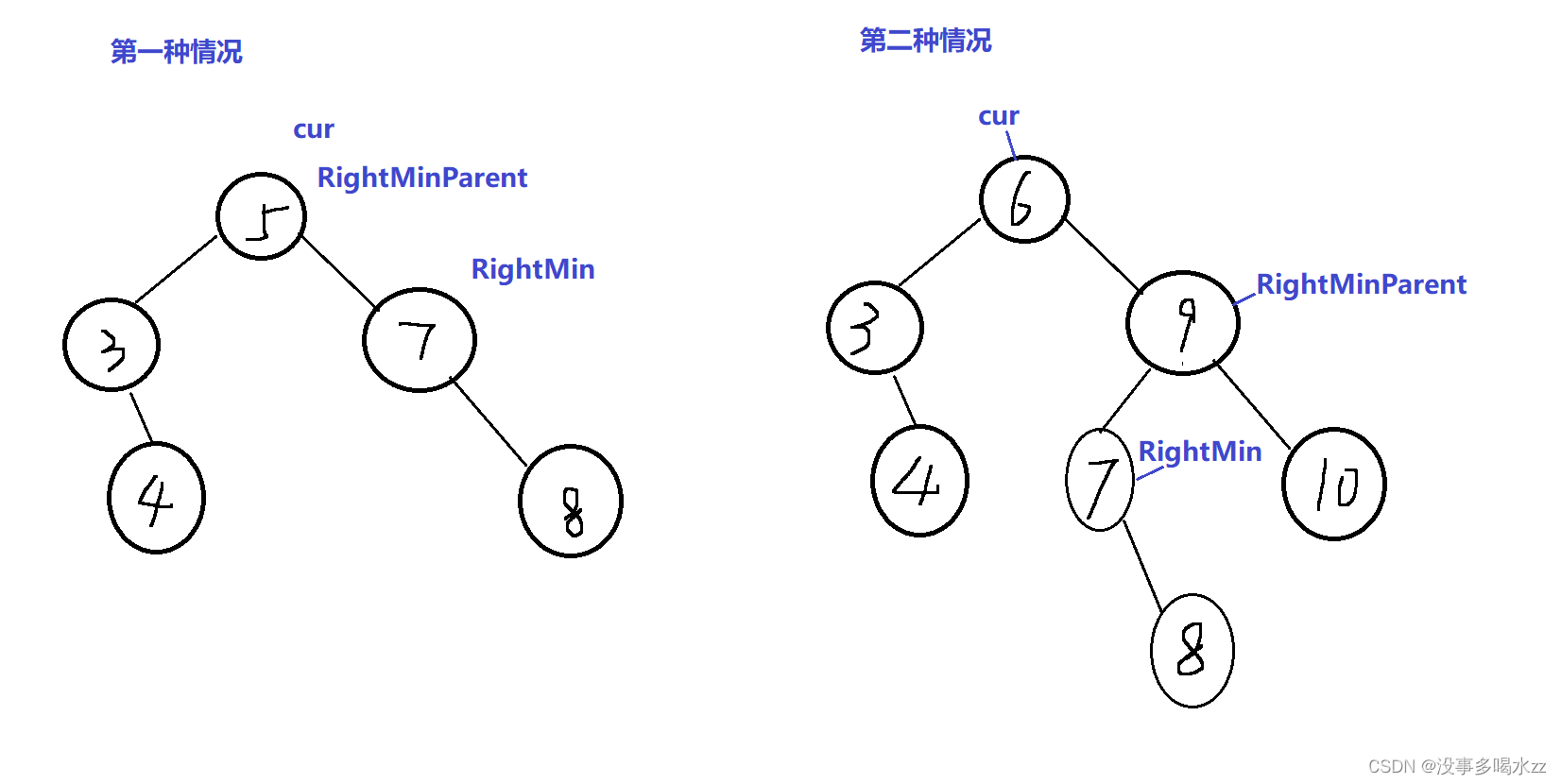
bool Erase(const K& key)
{
	// 删除分为3个情况
	// 1.删除节点只有左孩子 2.删除节点只有右孩子(没有孩子包含在这两种情况)  3.既有左孩子又有右孩子
	Node* parent = _root;
	Node* cur = _root;
	while (cur)
	{
	    // 先找节点，找到了才有后面的删除操作，否则要返回false
		if (cur->_key > key)
		{
			parent = cur;
			cur = cur->_left;
		}
		else if (cur->_key < key)
		{
			parent = cur;
			cur = cur->_right;
		}
		else   //此时进行删除
		{
			if (cur->_left == nullptr)  //无左孩子
			{
				if (cur == _root)   // 只有一个根节点
					_root = cur->_right;
				else if(cur == parent->_left)   // 这个节点为parent的左孩子的情况
				{
					parent->_left = cur->_right;
				}
				else if (cur == parent->_right) // 这个节点为parent的右孩子的情况
				{
					parent->_right = cur->_right;
				}
				delete cur;
			}
			else if (cur->_right == nullptr)  // 无右孩子
			{
				if (cur == _root)
					_root = cur->_left;  // 直接让左孩子作为根就可以了
				else if (cur == parent->_left)
				{
					parent->_left = cur->_left;
				}
				else if (cur == parent->_right)
				{
					parent->_right = cur->_left;
				}
				delete cur;
			}
			else  // 此时为左右孩子都有的情况
			{
				Node* RightMinParent = cur;
				Node* RightMin = cur->_right;
				while (RightMin->_left)
				{
					RightMinParent = RightMin;
					RightMin = RightMin->_left;
				}

				swap(RightMin->_key, cur->_key);
				swap(RightMin->_value, cur->_value);
				
				if (RightMinParent->_right == RightMin)   // 特殊情况得特殊处理
					RightMinParent->_right = RightMin->_right;
				else
					RightMinParent->_left= RightMin->_right;  //此时，RightMin
				//只可能有右孩子，因为它是最小的右子树节点(不能有比它更小的了)
				delete RightMin;
			}
		}
		return true;
	}
	return false;
}

InOrder遍历二叉树操作

这里我们需要注意两个点： 第一个是如何遍历，也就是我们调用采用递归的方法。
第二个是为什么我们这里要封装一层，而不是直接用，直接传值root并接收。 因为root是一个私有变量，我们在类外是无法访问到的，此时我们要执行遍历操作又必须得从根开始。想访问到，就需要通过函数进入到内部，才能访问到这个私有变量。

	void InOrder()  // 为什么这里要封装一层而不是直接传入root，因为root是私有成员，
	//我们在外面传参时是访问不到这个私有成员变量的。我们只有通过函数进入到类内，
	//才能访问到root，并传参给包了一层的InOrder函数
	{
		_InOrder(_root);
		cout << endl;
	}
private:
	void _InOrder(Node* root)
	{
		if (root == nullptr)
			return;
		_InOrder(root->_left);
		cout << root->_key << ":" << root->_value << endl;
		_InOrder(root->_right);
	}

模拟字典

下面的代码可以用来模拟字典操作

BSTree<string, string> dict;
dict.Insert("insert", "插入");
dict.Insert("erase", "删除");
dict.Insert("left", "左边");
dict.Insert("string", "字符串");
dict.Erase("insert");
dict.Erase("string");
string str;
while (cin >> str)
{
	auto ret = dict.Find(str);
	if (ret)
	{
		cout << str << ":" << ret->_value << endl;
	}
	else
	{
		cout << "单词拼写错误" << endl;
	}
}

模拟统计次数

下面的这个代码，可以用来统计次数

	string strs[] = { "苹果", "西瓜", "苹果", "樱桃", "苹果", "樱桃", "苹果", "樱桃", "苹果" };
	// 统计水果出现的次
	BSTree<string, int> countTree;
	for (auto str : strs)
	{
		auto ret = countTree.Find(str);
		if (ret == NULL)
		{
			countTree.Insert(str, 1);   // 不存在就插入
		}
		else
		{
			ret->_value++;  //存在就让value++
		}
	}
	countTree.InOrder();