线性表的查找算法

一、顺序查找：最基本的查找方法，从头到尾一一比对。

int SearchSequent(int *a, int n, int key){
    int i;
	for(i = 1; i < n; ++i){   //数据从下标为1处开始存储，查找成功则返回下标，失败则返回0
		if(a[i] == key) 
             return i;
	}
	return 0;
}

此代码使用for,每次循环都要判断i是否小于n。所以可以设置一个哨兵对此进行优化。

int SearchSequent(int *a, int n, int key){
    int i;
	a[0] = key;  //令a[0]=key,设置哨兵
	i = n;       //循环从数组尾部开始
	while(a[0] != key)
         i--;
	return i;
}

二、有序表查找：

1、折半查找：又称二分查找，在一个有序的顺序表上（假设是升序），判断要查找的值和中间值大小关系，如果要找的值大于中间值，就说明要找的值如果存在那么必然在中间值的右边，反之亦然，随后再拿查找值和中间值右边数据的中间值比较，直到找完或者找到，该算法的时间复杂度是O(logn)。

int Binary_Search(int *a,int n,int key){
	int low=1,high=n;
	int mid;
	while(low<=high){
		
		mid=low+(high-low)/2;
		if(a[mid]==key){
			return mid;
		}
		else if(a[mid]>key){
			high=mid-1;
		}
		else {
			low=mid+1;
		}
	}
	return 0;
}

2、插值查找：根据要查找的关键值key与查找表中最大最小记录的关键字比较后的查找方法。

关键是求mid的公式，其他的与二分查找相同。

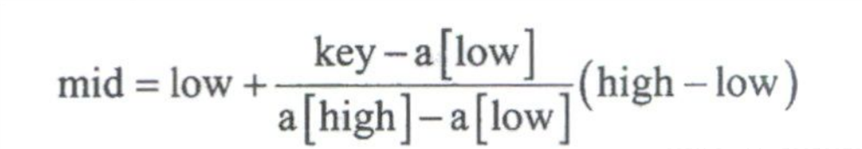
int InterpolationSearch(int *a,int n,int key){
	int low=1,high=n;
	int mid;
	while(low<=high){

		 // 避免除零错误
        if (a[high] == a[low]) {
            // 当区间内所有元素相同时，退化为线性查找
            for (int i = low; i <= high; i++) {
                if (a[i] == key) return i;
            }
            return 0;
        }

		mid = low + (high - low) * (key - a[low]) / (a[high] - a[low]);
		if(a[mid]==key){
			return mid;
		}
		else if(a[mid]>key){
			high=mid-1;
		}
		else {
			low=mid+1;
		}
	}
	return 0;
}

三、线性索引查找:索引就是将一个关键字与它对应的记录相关联的过程，所谓线性索引就是将索引项集合组织为线性结构，也称为索引表。

分块索引：将n个数据元素“按块有序”划分为m块（m<=n）。

条件：1）块内无序

           2）块间有序

定义分块索引的索引结构体：

struct IndexBlock{
	int maxval;    //最大关键码
	int startpos;  //首元素的位置
	int count;     //块中元素的个数
};

 代码如下：

#include<iostream>
using namespace std;
struct IndexBlock{
	int maxval;
	int startpos;
	int count;
};
int findBlock(IndexBlock* b,int k,int key){ //查找关键值属于哪个区，类似于二分查找，但是有区别 
	int low=0,high=k-1;
	int mid;
	
	while(low<high){
		mid=low+(high-low)/2;
		if(b[mid].maxval>key){
			high=mid;    //high不是mid- 1而是 mid 
		}
		else if(b[mid].maxval<key){
			low=mid+1;
		}
		else{
			low=high=mid;
		}
		//cout<<low<<" "<<high<<endl;
	}      //当循环结束时low=high,low和high的值就是key所属区块的下标 
	return low;
}
int BlockSearch(int *a,IndexBlock* b,int n,int k,int key){
	
	int index=findBlock(b,k,key);
	
	int i;
	for(i=0;i<b[index].count;i++){   //这里直接使用顺序查找 
	
		if(a[i+b[index].startpos]==key) 
		    return (i+b[index].startpos);
	}
	return 0;
}

int main(){
	int n,i;
	int k;
	int *a;          
	IndexBlock* b;   
	cin>>n; 
	a=new int[n+1];
	for(i=1;i<n+1;i++){       //从下标1开始存储 
		cin>>a[i];	
	}
	cin>>k;              //将数组分为k块 
	b=new IndexBlock[k];
	for(i=0;i<k;i++){    
		cin>>b[i].maxval;
		b[i].startpos=n/k*i+1;      //这里条件是数组a可以被均匀分块 
		b[i].count=n/k;
		
	}
	int key； 
	cin>>key;    
	cout<<BlockSearch(a,b,n,k,key)<<endl; 
	return 0;
} 

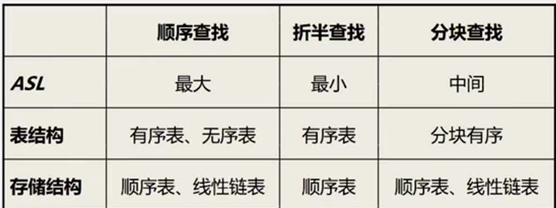
三种方法对比：