剑指OFFER笔记_10_1_斐波那契数列_JAVA实现（非递归）

题目：

• 求斐波那契数列的第n项

解题思路

• 各类课程都用递归的方式来演示，而且通常利用这道题作为递归的引入用例。
• 递归拥有代码简洁的优点，但是效率上较低。因为递归在函数中不断调用自身，在每一次调用的过程中，都要往内存栈中分配空间来保存参数，返回地址以及临时变量，而且往栈中压入和取出数据都需要时间，所以效率较低。
• 而且递归的过程中，还会不断计算相同的值，比如计算fib(10)，需要计算fib(9)+fib(8)，而fib(9)需要计算fib(8)+fib(7)，此时fib(8)就是被重复计算的值，当计算的n足够大时，被重复计算的数是指数增长的，这显然是不可接受的。
• 递归的算法都可以用循环来代替。自下而上的循环计算，将每个n较小的fib(n)先存好，这样就不需要重复计算了。

代码

函数主体部分代码

package q10_1;

/**
 * 求斐波那契数列的第n项
 * @author asus
 *
 */
public class Solution {
	public static int fib(int n) {
		//第0项值为0
		if(n == 0)
		{
			return 0;
		}
		//第1项为1
		if(n == 1)
		{
			return 1;
		}
		
		//从第二项开始考虑
		//预储存第1项
		int fibSmaller = 0;
		//预储存第2项
		int fibBigger = 1;
		int temp = 0;
		for(int i = 2; i <= n; i++)
		{
			temp = (fibSmaller + fibBigger) % 1000000007;
			//大项作小项
			fibSmaller = fibBigger;
			//之前的大项小项和作为大项
			fibBigger = temp;
		}
		
		return temp;
    }
}

测试部分代码

package q10_1;

public class TestApp {

	public static void main(String[] args) {
		// TODO Auto-generated method stub
		//求数列中的0-20项
		for(int i = 0; i <= 20; i++)
		{
			System.out.println("数列中第" + i + "个数是： " + Solution.fib(i));
		}
	}

}

运行结果截图

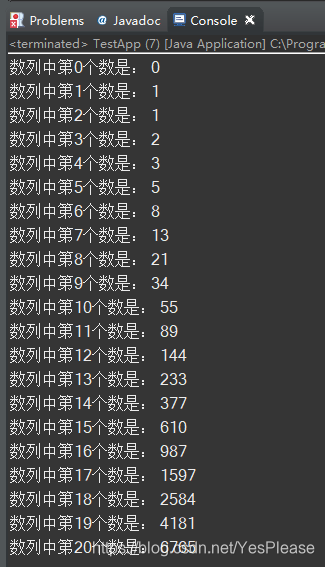
LeetCode运行截图