DSO全家桶（四）——DSO前端：前端跟踪

DSO前端跟踪

　　嗨，各位读者朋友们好！今天我们接着讲前端跟踪。由于第三讲中的初始化部分包含trackFrame估计初始两帧运动，与本讲内容重叠，因此笔者将其初始化中的跟踪合并到当前讲中，具体的区别稍后我们会在介绍跟踪流程的过程中叙述。

　　OK，我们还是一如既往地先上个流程图，如图1所示。笔者始终认为只有把流程图画清晰了，才能说明自己对整个流程足够了解。在写博客的时候，流程图有助于梳理思路，便于读者们更加清楚地知道整个运行逻辑。

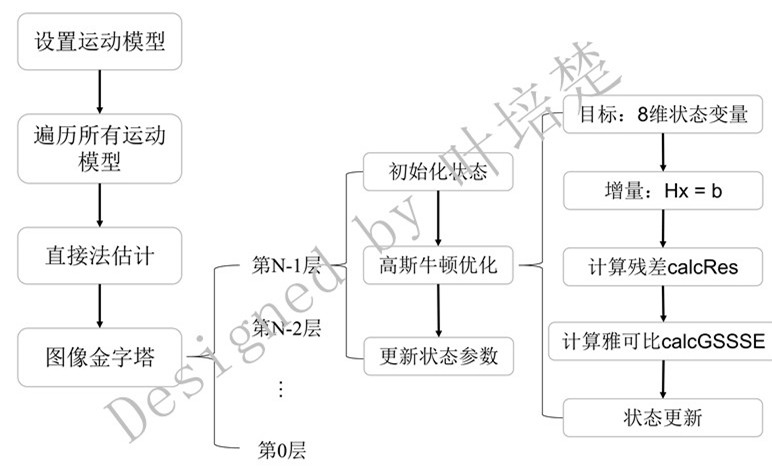
                                                     图1. DSO前端跟踪流程

　　特征点法SLAM中可以通过首先进行参考帧和当前帧的特征点匹配找到匹配对，构建数据关联关系，从而估计相对运动。而基于直接法的DSO前端跟踪，却没有这么方便了，因为直接法中的点都是局部梯度较大的点，除此之外并无其他显著特征，因为无法做重投影误差。而直接法的策略是将参考帧中所有点(提取到的梯度点)投影到当前帧中，构建光度误差函数，联合优化。那么这里，有个问题就需要特别注意了，直接法无法构建数据关联关系，那么初始的相对运动就无法确定，所以直接法需要首先设置运动模型，才能继续后面的步骤。

　　接下来，我们按照图1来大致梳理一下DSO前端跟踪的思路：

　　1. 设置运动模型，如前所述，需要根据先验值给出运动模型。

　　　　在DSO初始化阶段，这个先验值被设置为旋转单位阵、位移零向量，表示两帧间完全重合的意思。

　　　　在DSO常规的跟踪阶段，这个先验值通常是由前面几帧确定的，比如前一帧和前前帧之间的相对运动作为当前帧的运动模型，称为单倍速运动模型。DSO还添加了两倍速、0.5倍速模型，此外还有在此基础上的一些较小的旋转模型等。

　　2. 遍历所有运动模型，对于每个运动模型都执行后续的直接法估计。只有前面存在满足要求的运动模型时，后续的模型才不会被继续验证，跳出循环。若是所有运动模型都不满足要求，则说明跟踪丢失。

　　　　在DSO初始化阶段，循环迭代会设置跳出条件，除了满足收敛或者迭代次数达到最大值这两种情况，初始化阶段还设置了一个fails次数，若次数过多，则当前初始化失败，重新开始。

　　　　在DSO常规的跟踪阶段，循环迭代设置的跳出条件是满足收敛条件或者迭代次数达到最大值。若最终阈值不满足条件，则验证下一个运动模型。

　　3. 直接法运动估计，采用的是有点类似于光流的方法，在这里需要用到图像金字塔，目的是为了节省计算时间。

　　　　从图像金字塔最顶层开始估计相对运动，并逐渐向下传播。值得注意的是，我们在上一讲中提到了makeNN()这个函数，他的目的是创建每一层每个点的10邻域信息，并且关联其上一层的某个最近邻点。显然，在基于图像金字塔的跟踪过程，上一层的深度值可以传播到下一层作为初值，这便是第三讲的内容最重要的意义。

　　4. 高斯牛顿优化，这部分内容是整个跟踪过程最核心的，也是最难的。

　　　　已知：初始的运动模型、参考帧图像中的梯度点、参考帧和当前帧构建的光度误差函数。

　　　　问题：通过优化运动模型，使得光度误差函数的代价值最小。

　　　　求解策略：利用泰勒展开近似非线性函数，通过高斯牛顿法构建增量方程：$Hx = b$。后续便是基于schur消元法求解增量值，基于判断条件对运动模型进行更新。

　　在上面的四个主要流程中，最核心的便是第4个——高斯牛顿优化。我们会在这一讲着重介绍一下DSO中在直接法运动估计中，这个高斯牛顿法是怎样操作的。

---

直接法运动估计

　　在前面我们提到过，直接法不同于特征点法，可以通过特征匹配来构建数据关联关系。那么直接法通常的做法呢，是将两个参考图像中提取到的梯度点全部投影到当前图像中，通过调整位姿和光度仿射模型使得两帧图像间的光度误差值最小。

　　为了更好地描述问题，我们会采用数学符号来完成这一讲的内容。在此之前呢，我们要先定义一下符号。(昨天吃饭的时候才刚跟范帝楷聊过这个事情)

　　假设我们当前有参考帧  和当前帧 ，参考帧中的光度仿射参数为 ， 同理，当前帧的为 。相机内参数矩阵为 ，由参考帧 的坐标系到当前帧 的坐标系相对变换的李代数为 ，并且我们有：

　　\begin{equation}
　　　　exp(\xi^{\wedge}_{cr}) = \begin{bmatrix}R_{cr} & t_{cr} \\ 0^{T} & 1\end{bmatrix}
　　\end{equation}

　　OK，那么我们接下来开始描述光度误差函数是怎么定义的。

　　对于单一的一个点，我们先不考虑DSO中描述的pattern，只单纯的考虑对于一个像素，这个光度误差函数怎么描述。

　　\begin{equation}
　　　　r = w((I_{c}[p_{c}] - b_{c}) - \frac{t_{c} e^{a_{c}}}{t_{r}e^{a_{r}}}(I_{r}[p_{r}] - b_{r})) = w(I_{c}[p_{c}] - a_{cr}I_{r}[p_{r}] - b_{cr})
　　\end{equation}

　　其中，点为参考帧 中梯度较大的点，表示点 在当前帧 中的反投影坐标。具体计算方法：

　　\begin{equation} \begin{aligned}
　　　　p_{c} &= KX_{c}^{'} \\ &= Kd_{c}X_{c} \\ &= Kd_{c}(R_{cr}X_{r} + t_{cr}) \\ &= Kd_{c}(d_{r}^{-1}R_{cr}K^{-1}p_{r} + t_{cr}) \\ &= Kd_{c}exp(\xi^{\wedge}_{cr})(d_{r}^{-1}K^{-1}p_{r})
　　\end{aligned} \end{equation}

　　在公式 中，我们定义了一些新的符号：

　　1. 点 在参考帧相机坐标系中的点表示为