数学建模之TOPSIS优劣解距离法

        上一份文章我们讲了层次分析法，具体请看博主的上一篇文章

https://blog.youkuaiyun.com/YYYSSSMMM0504/article/details/148292581

        层次分析具有比较多的局限性比如说决策层不能太多，太多的话n（n阶矩阵）较大，那么判断矩阵和一致矩阵差异较大。那么如果说决策层中的指标数据题目已经给了，指标数据已经给了，那么我们任何利用这些数据使得评价结果更加准确，这里up主给了一个例子

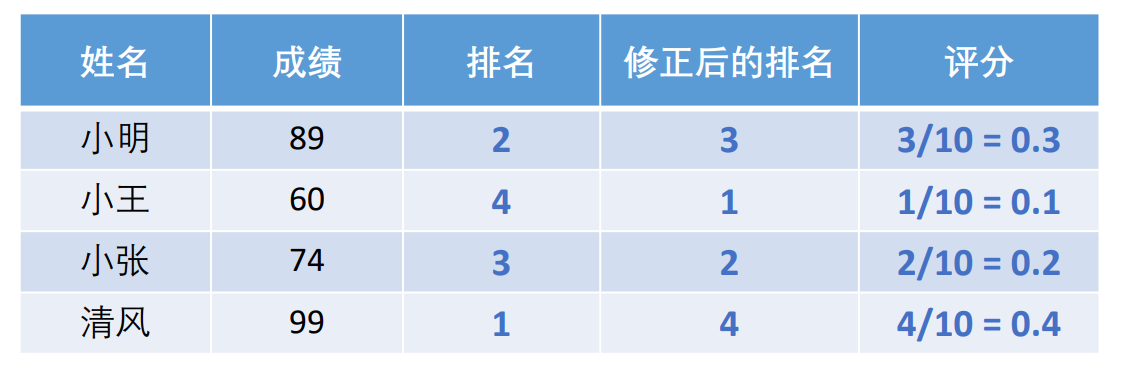
        我们给排名进行评分得到评分如上图所示。但是这样子评分存在一个问题就是无论小王多低分都是最后一名，那么小王无论考多低都是0.1，评分不能随着成绩变动，存在不合理的情况，即可以随便修改成绩，只要保证排名不变，那么评分就不会改变！

        所以up主换了个想法，构造一个计算评分比较合理的公式

        通过计算我们得到下表

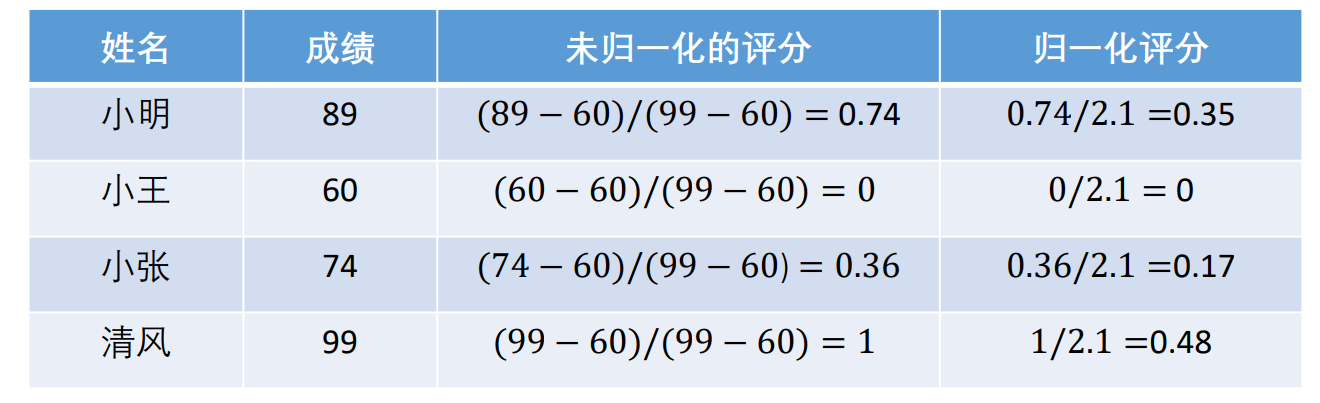
        归一化是什么意思？

        归一化（Normalization） 是将数据按比例缩放，使之落入一个特定的范围（如 [0, 1] 或 [-1, 1]），目的是消除数据量纲或分布差异的影响，使其更具可比性，适用于算法处理或分析。

        这种构造方法呢一般要满足三个条件。

        我们接着则拓展指标个数，指标存在极大型指标（本文提到的成绩，就是成绩越高越好）、极小型指标（清风UP主说到了情商吵架次数，吵架次数肯定是越小越好，越不怎么吵架的情商当然高）、中间型指标（PH值，越解决7越好）、区间型指标（适宜温度啥的）。仔细想想那么多种指标，我们得先统一指标类型。将所有指标转为极大型指标。

        那么不同类型的指标之间如何转换呢。极小型通过max-转换为极大型

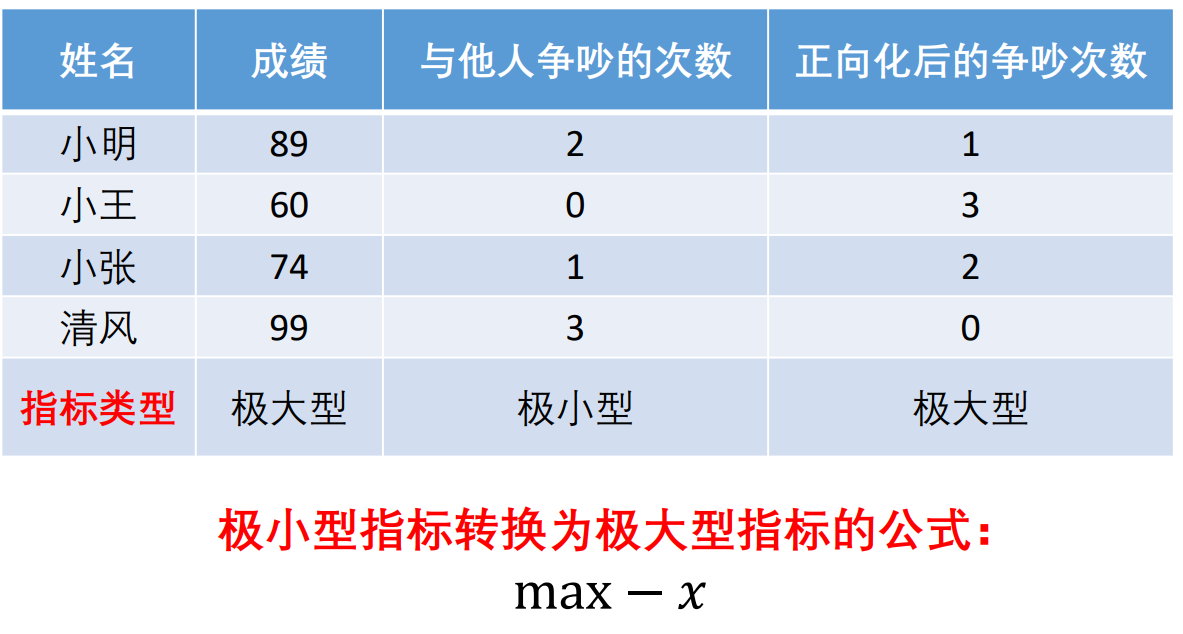
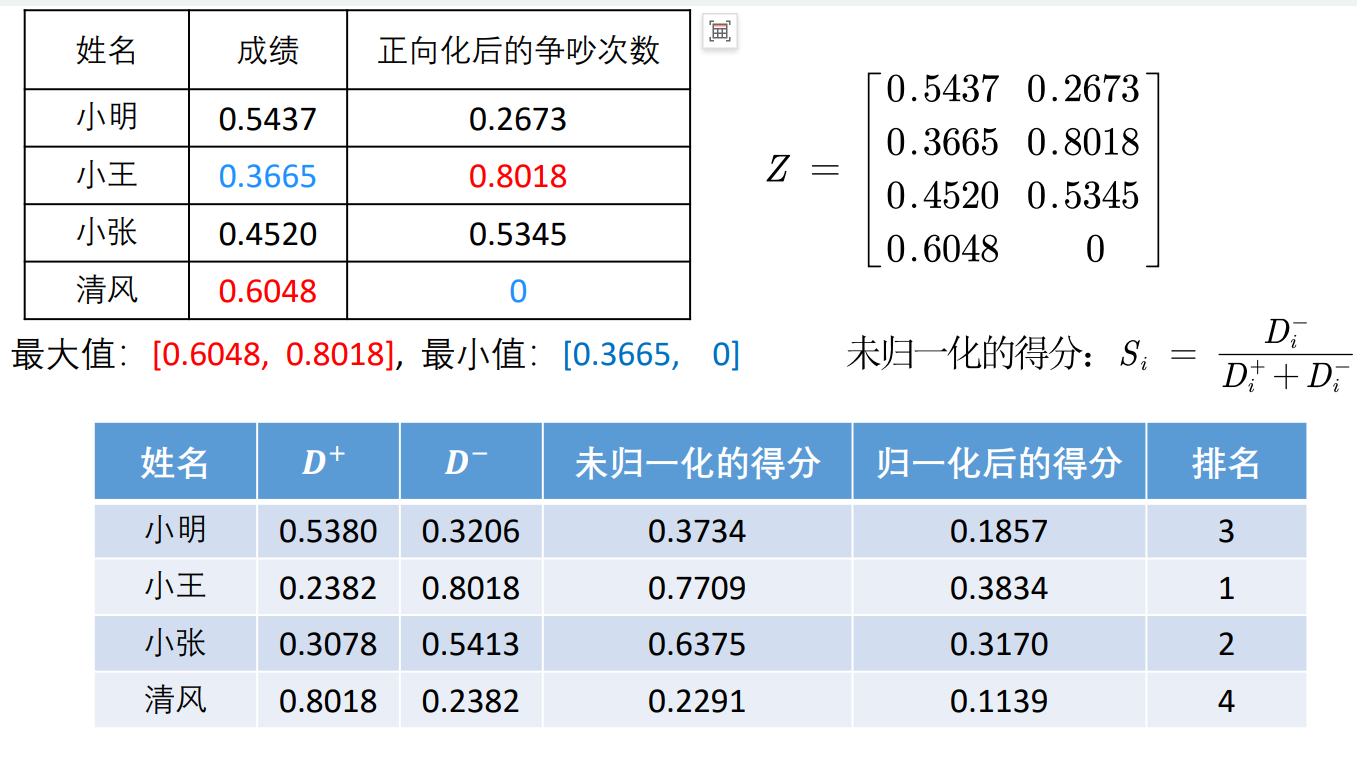
        我们现在有成绩和正向化后的争吵次数两个指标，为了消去两个指标不同量纲的影响，这里对矩阵进行标准化处理。

        最重要是公式是上述图像中框住部分。通过这样子计算量纲会被消除。

        标准化后，我们应该如何计算得分。当只有一个指标时

        回归我们的TOPSIS，是不是叫优劣解距离法，这个优相当于x与最大值的距离；劣相当于x与最小值的距离。类比多个指标计算。

通过公式就能求解出

        好，我们总结一下，TOPSIS是解决指标层题目已给数据我们通过对数据进行、正向化（转为极大型指标）、然后对正向化后的矩阵标准化（消除量纲影响）、计算得分并最后再归一化（得分归一化是不影响排序的）。