层次分析用于解决评价类问题,一开始我认为这个模型主观性还是太强直到重新学习后发现了层次分析法确实有点东西。层次分析主要要有一个框架图,包括目标层、准则层(指标)、方案层。具体图片如下图所示。
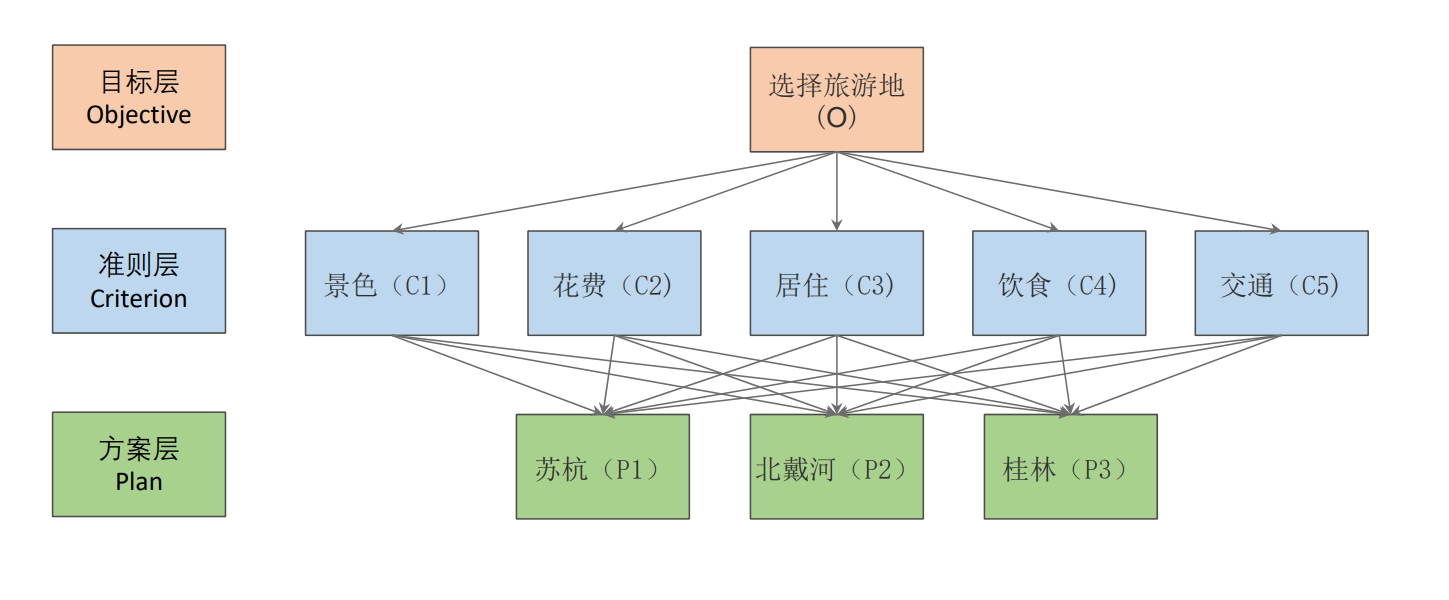 在讲层次分析之前我想先引入打分这个概念为什么是解决评价类的问题。我是跟着清风学的。他举了一个选大学的例子,为了上大学小明在武大和华科二选一,为了解决这个问题,他列出了四个他认为最重要的四个方面,包括学习氛围、就业前景、男女比例、校园景色四个指标。分别给了四个指标对应权重(这里权重是小明自己填的,和为1)。
在讲层次分析之前我想先引入打分这个概念为什么是解决评价类的问题。我是跟着清风学的。他举了一个选大学的例子,为了上大学小明在武大和华科二选一,为了解决这个问题,他列出了四个他认为最重要的四个方面,包括学习氛围、就业前景、男女比例、校园景色四个指标。分别给了四个指标对应权重(这里权重是小明自己填的,和为1)。

整理好表格后,小明进行填写
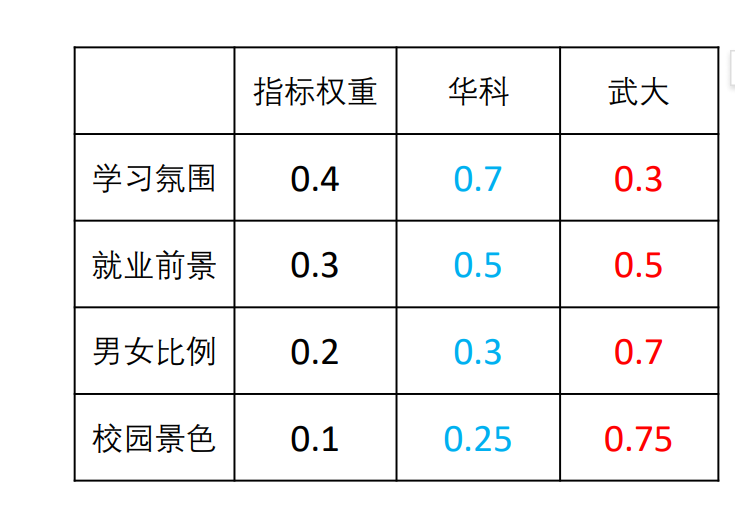
最后结果得到如上表所示。此时已知权重与打分,通过计算可以的知道,华科最终得分高于武大于是小明选择了华科。所以我们回归正题,这是一个评价类题目在小明心中 ,为了解决评价类题目小明采取了打分解决。
这里再举了一个例子,我现在想旅游,为了旅游我出了三个方案,即苏杭、北戴河、桂林三个方案。对于每个方案我存在有关景色、花费、居住、饮食、交通等指标。
我们静下来进行思考,如要一个人填写下面如此多的指标,会不会出现前一秒一个想法后一个想法(大家有没有填过一些问卷,是不是觉得很多时候会前一秒一个想法后一秒一个想法反正我是有点)。
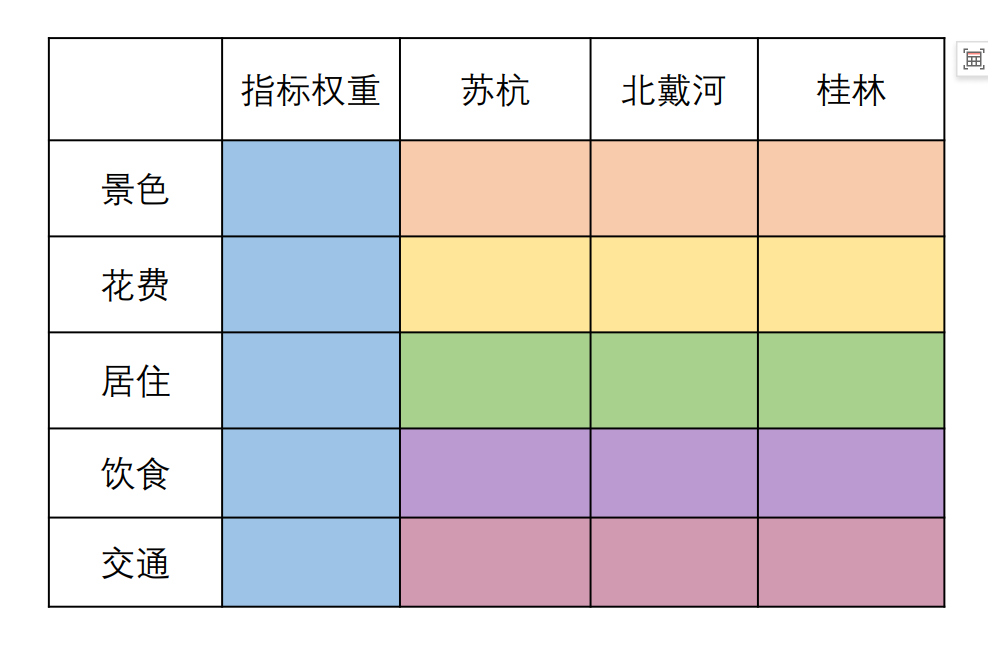
后面我查了一下司老师的书,确实提到了主观能动性还是太强了。

为了解决上述提到这个问题,我们采取一种新的解决方案。这是一个分而治的方法,一次性考虑五个指标往往出现考虑不周的状况。解决方法就是,两个两个指标进行比较,最终根据两两比较的结果来推算出权重。这就是层次分析法的思想。这样主观能动性是不是稍微低一点了。
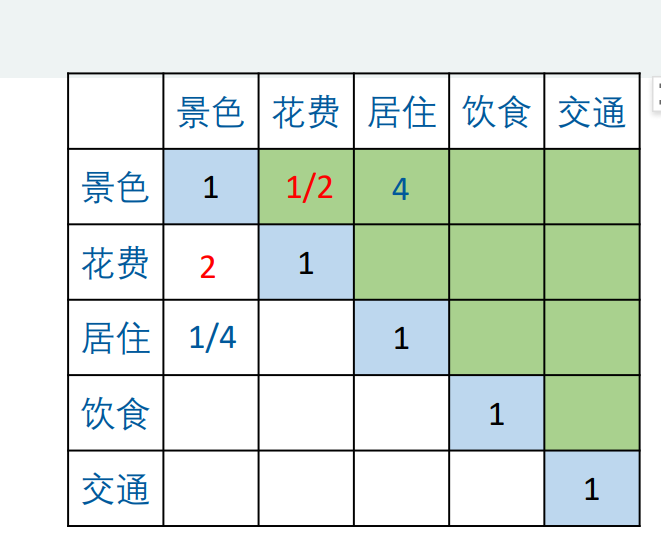
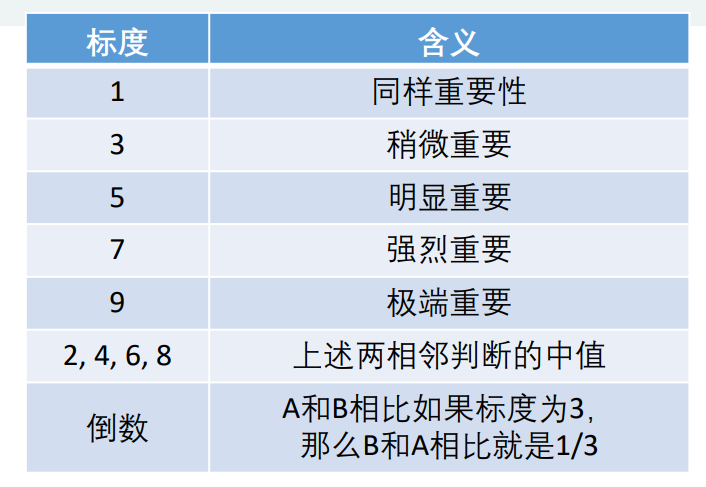
这个表格填写就是对比,权重两两比较,举例这里的花费比景色稍微重要(1-3之间),景色比居住明显重要(3-5之间)。具体可以看上面的标度进行填写。
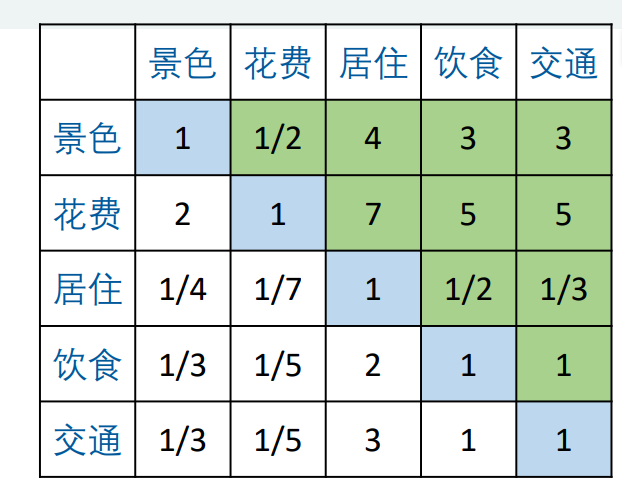
我们填好之后发现这是一个正互反矩阵,什么是正互反矩阵呢,就是aij*aji=1。线性代数内容这里不多讲。上面填好的就是我们的判断矩阵了。得到判断矩阵我们就能很好计算权重,等会讲。
我们想计算杭、北戴河与桂林在景色方面所占的权重(得分),也是填这个判断矩阵。但是填写过程中我们发现这可能出现一个问题。
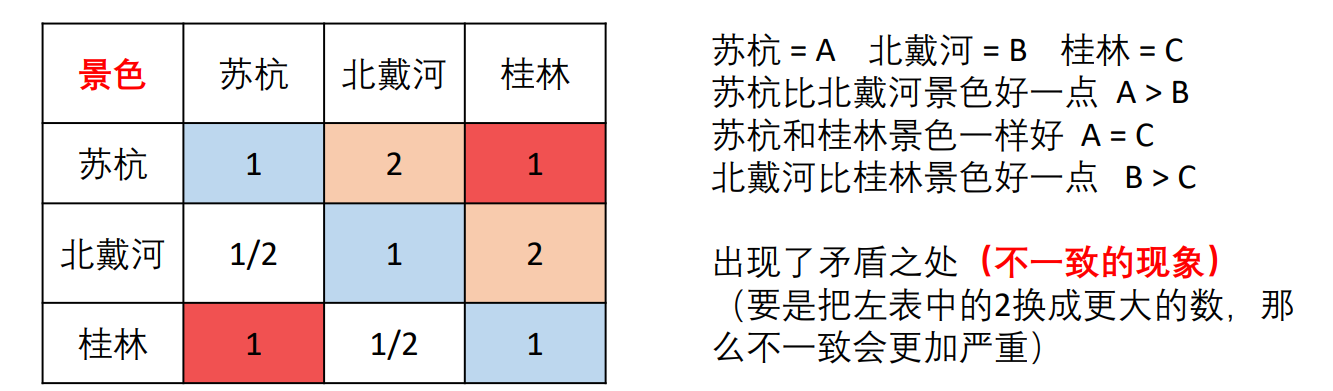
为了避免上述问题,我们引入一个新的矩阵叫一致矩阵。一致矩阵有的特点是各行(各列)之间成倍数关系。具体一致矩阵的概念看下图。在使用判断矩阵求权重之前我们必须进行一致性检验。

如果正互反矩阵为一致矩阵,那么特征值为n;不为一致矩阵,那么特征值一定满足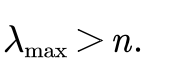
通过代码计算,发现判断矩阵越不一致时,最大特征值与n相差就越大。
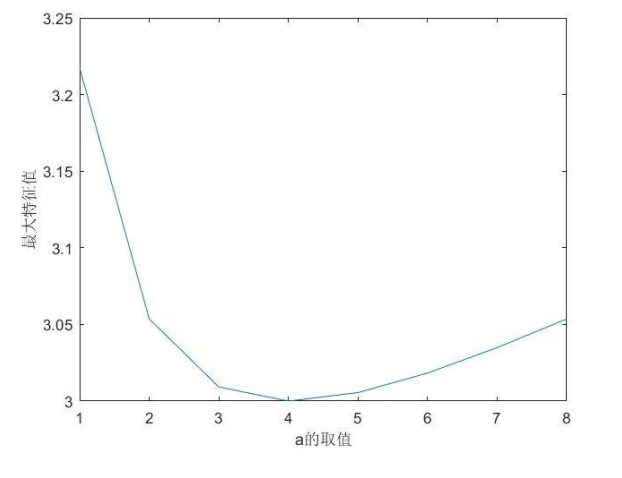
具体可视化图像如上图所示。
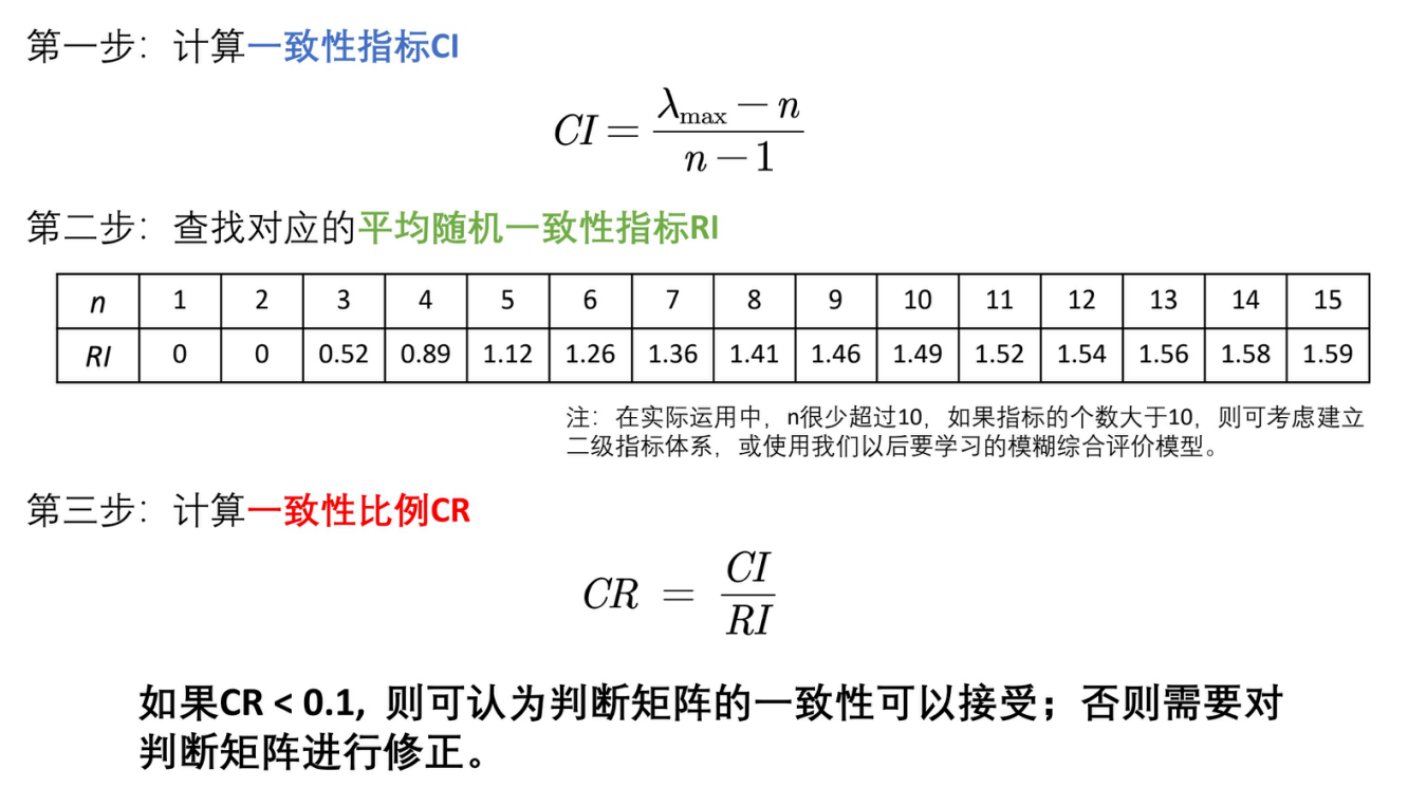
下面进行一致性检验步骤讲解。第一步计算一致性指标CI,CI的公式如图所示。第二步,查找对应的平均随机一致性RI(这个是资料可查的)。第三步是计算一致性比例CR,根据公式计算结果与0.1进行对比,如果CR<0.1,可以认为判断矩阵的一致性可以被接收,否则需要对判断矩阵进行修正。
我们再重新顺一遍,我们存在多个指标,对指标我们进行填写得到判断矩阵。判断矩阵一定是一个正互反矩阵,但不一定是一致矩阵,我们就要对矩阵进行一致性检验只有当检验通过时,我们才能根据矩阵求解相关权重。
那么如果判断矩阵是一个一致矩阵(肉眼可见)我们应该如何计算权重呢?此时判断矩阵仅仅只需要第一列的数据进行计算。具体结果如下图所示。
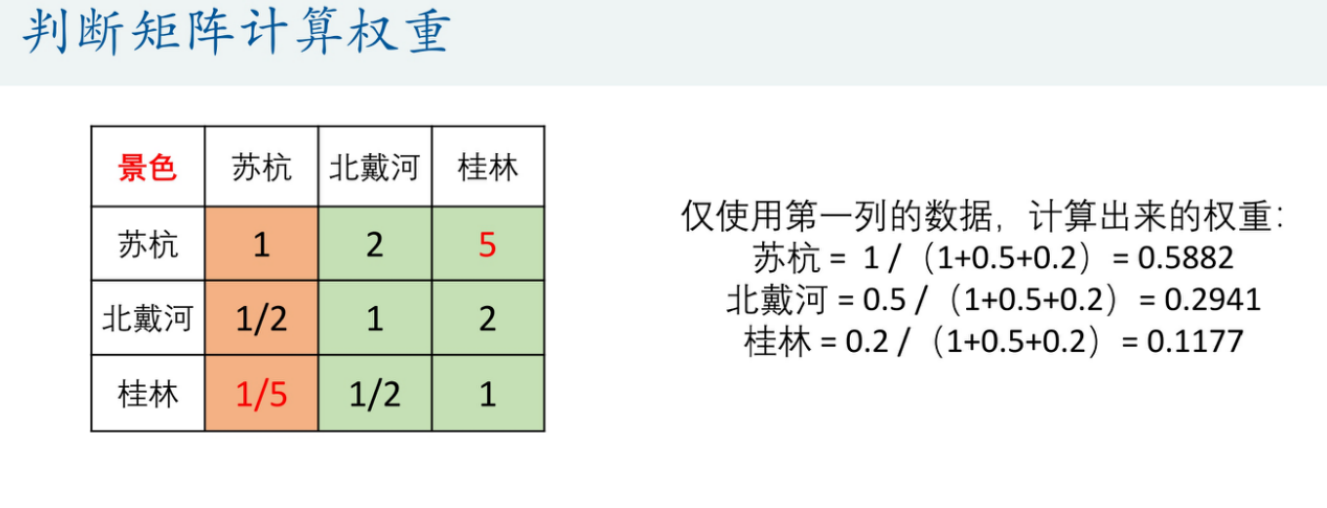
但是,如果我们的矩阵不是一致矩阵呢?此时判断矩阵就得将每一列都求解出来。然后算术加权求和求权重。具体计算请看下图。
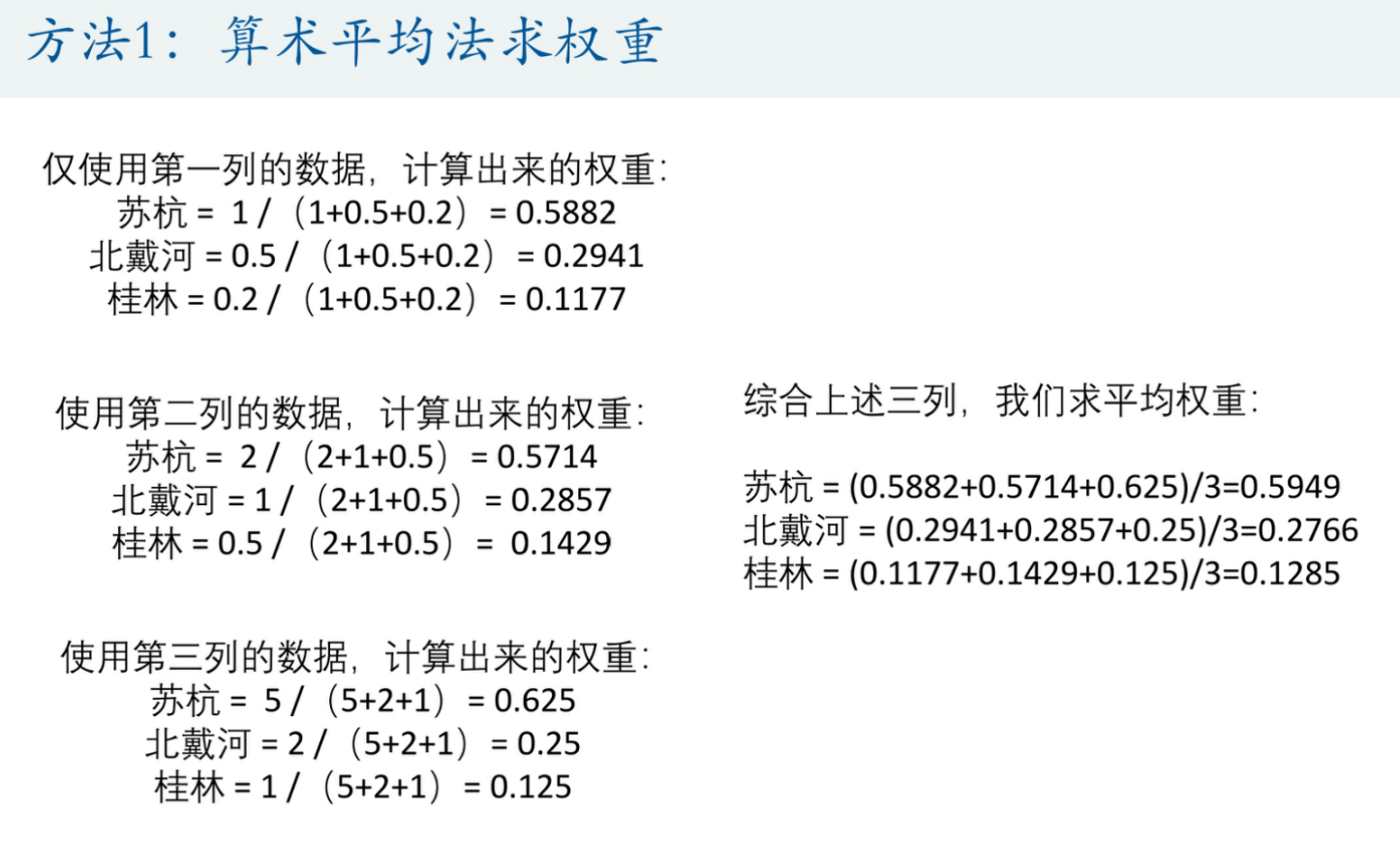

除了算术平均求权重这种方法之外,我们还有几何平均求权重、特征值求权重两种方法、几何不咋用到,我们打比赛的时候直接提一嘴也用上就好,UP主说的大家都只用特征值,就你最勤奋三个都用,印象分扛扛的。不闲聊了继续讲这个特征值求权重这个方法。

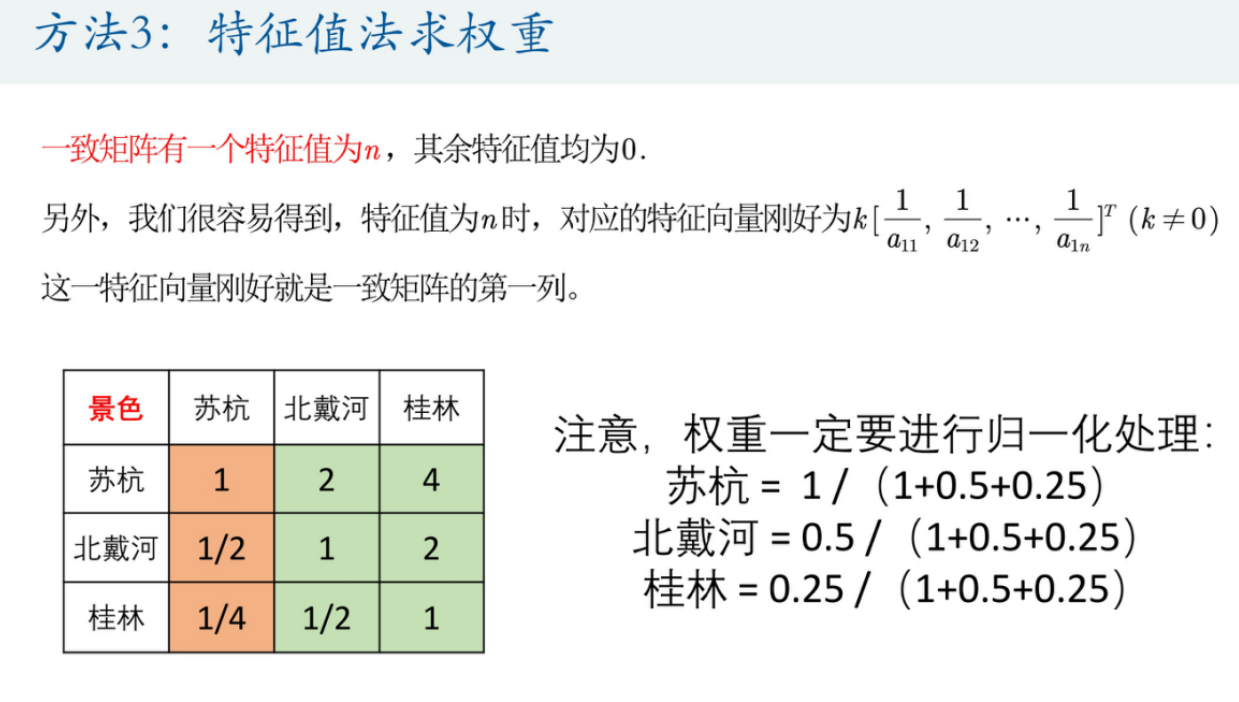
如果这是一个一致矩阵,那么此时特征向量为第一列数值。我们通过求解判断矩阵的特征向量,进而求出相应权重。具体结果如上图所示。
总结一下,解决评价类题目,我们要想到以下三个问题
①我们评价的目标是什么?
②为了达到这个目标我们有几个可选的方案?
③评价的准则或者说指标是什么?
好了,层次分析相关内容我都给整到这里了。我们下次讲讲旅行商TOPSIS问题,他对比层次分析来说,他的数据就没有那么主观(我们一般可以去搜知网查阅相关文献然后来填我们的判断矩阵),而是题目自带的。下次见,蓝桥杯就不更新了,只拿了省二


























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








