数学建模之插值算法

 在我看来，插值算法十分常见。像国赛或者说是其他数学建模类的比赛经常就是会给部分数据，比如某些数据只给单数月份而其他则是完整的所有月份数据。为了对齐统一度，我们需要对单数月份的数据进行插值处理，使得所有双数月被填充。

        插值法有三类，第一类是这个拉格朗日插值法

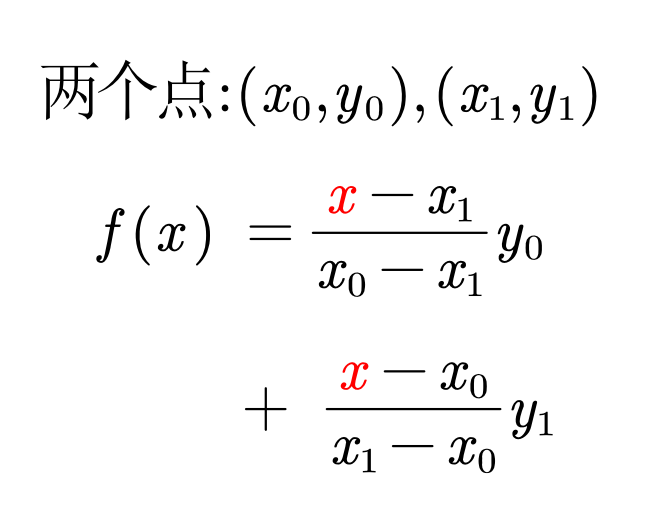
        其中x分别为对应的两个点。在数值分析中，拉格朗日插值法是以法国十八世纪数学家约瑟夫∙路易斯∙拉 格朗日命名的一种多项式插值方法。在若干个不同的地方得到相应的观测值， 拉格朗日插值法可以找到一个多项式，其恰好在各个观测的点取到观测到的值（取自清风数学建模）。

        如果此时我们对三个点进行插值则会有下方的式子。

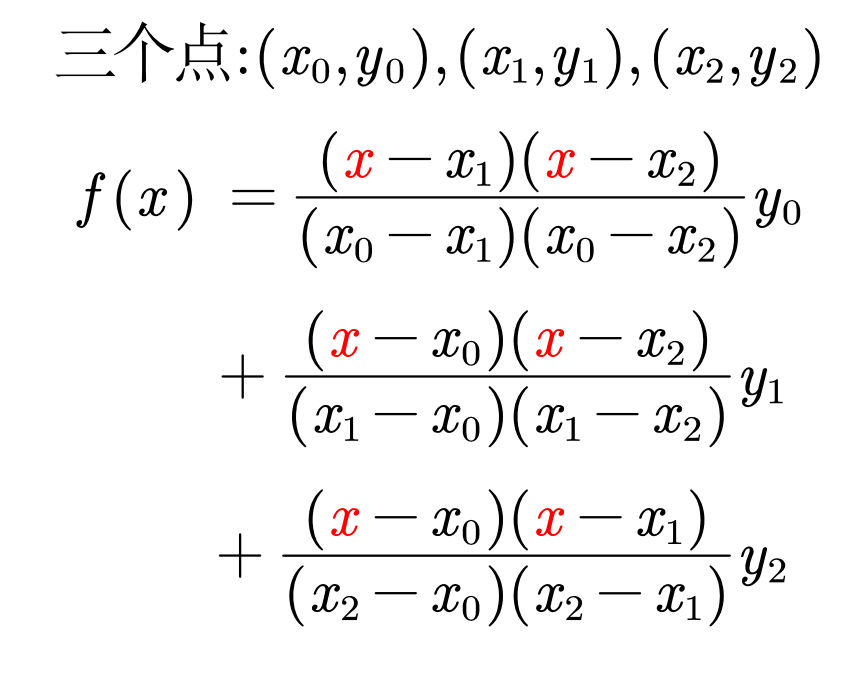
对下方四个点进行插值，则会有下方这个式子。

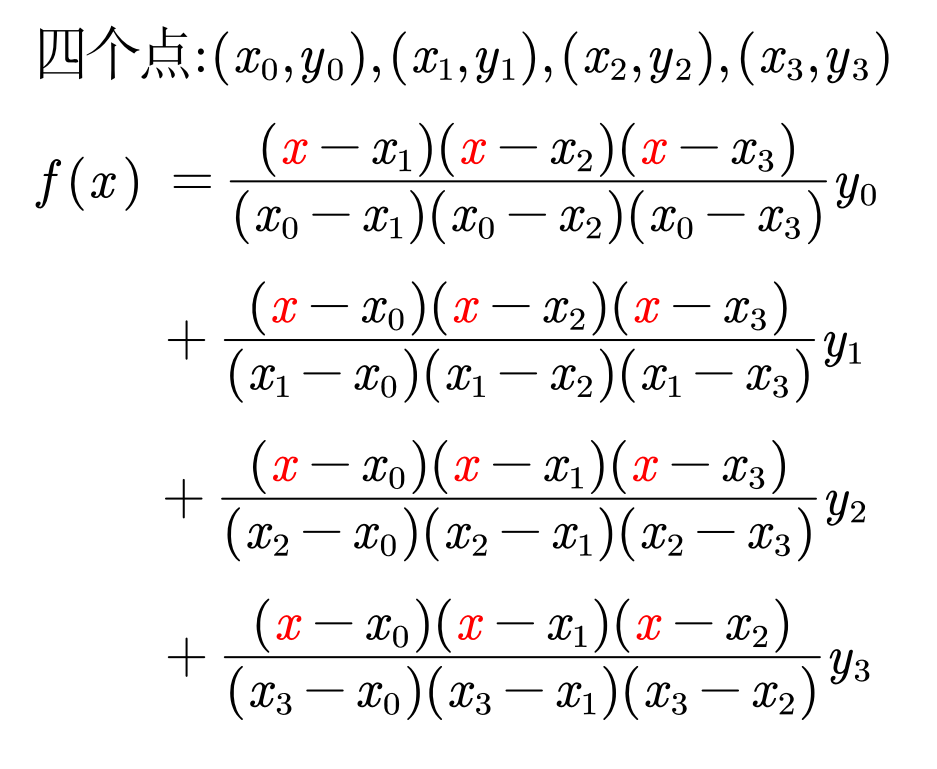
 我们总结一下，拉格朗日插值多项式有如下式子

        然而，拉格朗日插值会出现龙格现象，特别是高次插值。即在两端处波动极大，会产生明显震荡，在不熟悉的曲线运动趋势前提下，不要轻易使用高次插值。

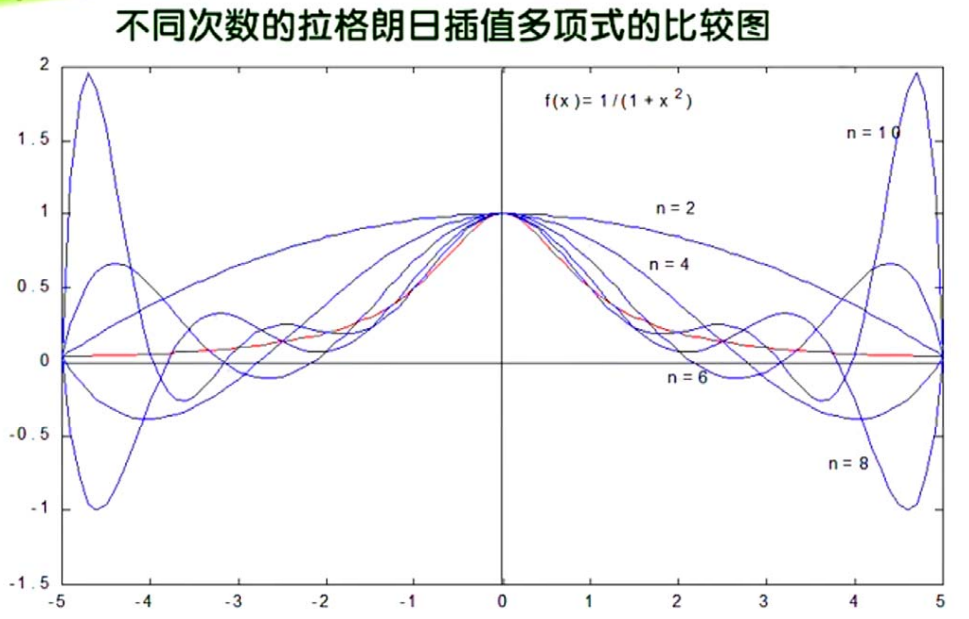
牛顿插值法是通过差商叠加实现的。具体如下图

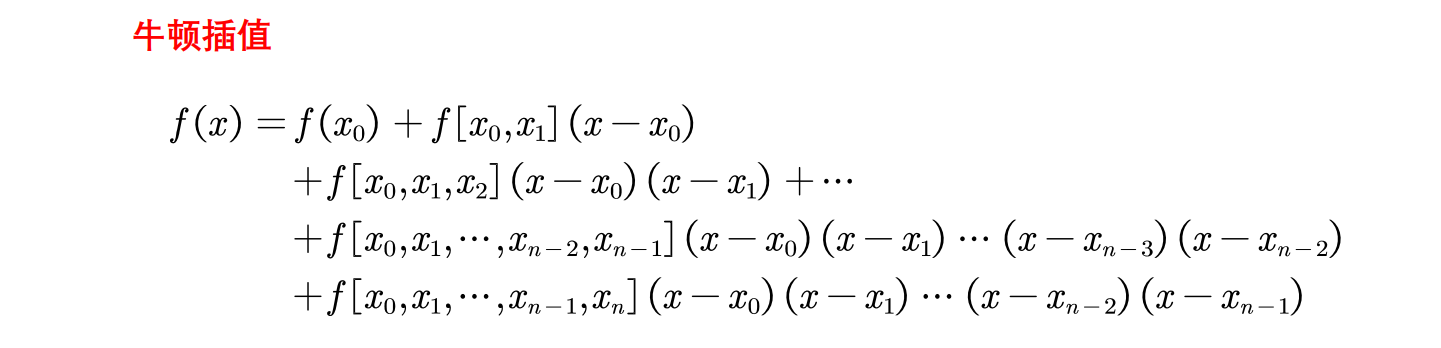
        对比拉格朗日插值，每增加一个点就要重新构造一个新的函数使得所有点全部经过此函数。而牛顿插值相对来说只需要再上一个式子基础上，增加多一句即可。

        与拉格朗日插值法相比，牛顿插 值法的计算过程具有继承性。 （牛顿插值法每次插值只和前n项 的值有关，这样每次只要在原来 的函数上添加新的项，就能够产 生新的函数。然而，牛顿插值也不能解决龙格问题。

        问题一即插值多项式次数高精度未必显著提高。问题二即多项式次数越高摄入误差可能显著增大。为了解决问题一与二，我们提出了分段低次插值，可以提高插值精度。

        接下来我想介绍埃尔米特插值，埃尔米特插值满足对应的导数值相等，高阶导数也相等。但是直接使用埃尔米特插值得到的多项式次数较高，也还是存在龙格现象。因此在实际应用上，我们还是用分段三次埃尔米特插值比较多。

matlab有内置函数

p=pchip(x,y,,newx)

其中，x是样本点横坐标，y是样本点纵坐标，而newx是准备插入的横坐标。

三次样条插值是一种特殊的插值方法。

        当满足上述三个条件时，我们可以构造三次样条插值函数。matlab也有内置函数，我们只要会使用即可。

p = spline (x,y, new_x) 

x是已知的样本点的横坐标;y是已知的样本点的纵坐标;new_x是要插入处对应的横坐标。

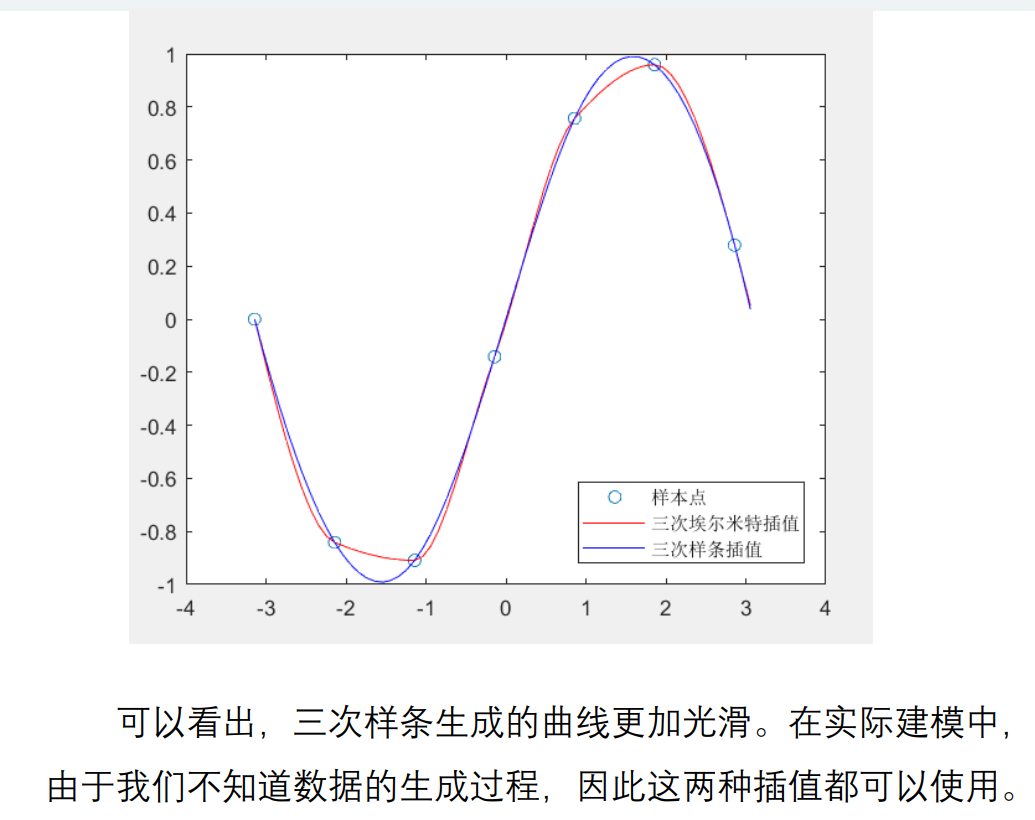
        可以看出三次样条插值的曲线更光滑，但在实际建模中由于我们不知道数据的生成过程，所以两种插值都可以用。（清风原话）