【矩阵论总结(1)】特殊的矩阵

1、零矩阵：元素全为零的矩阵

2、行矩阵：只有一行的矩阵

3、列矩阵：只有一列的矩阵

4、方阵：行数和列数都等于n的矩阵

5、对角矩阵：主对角阵以外的元素都为零的方阵

6、单位矩阵：主对角线元素全为1，其余元素全为零的方阵（表示为E或I）

7、逆矩阵：设A是n阶矩阵，若存在n阶矩阵B使AB=BA=E，则称A是可逆的，并称B是A的逆矩阵

8、正交矩阵：如果实方阵Q满足

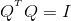        或，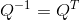

      则称Q为正交矩阵（正交矩阵是非奇异的，正交矩阵的逆矩阵仍是正交矩阵）

9、实对称矩阵：元素都是实数，且该矩阵的转置等于其本身

10、酉矩阵：酉变换在酉空间的标准正交基下的矩阵A是酉矩阵

11、Hermite矩阵：Hermite变换（酉对称变换）在酉空间的标准正交基下的矩阵，即有

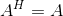       （Hermite矩阵的特征值都是实数）

12、正规矩阵：设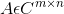，且等式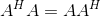成立，则A是正规矩阵（正交矩阵、对角矩阵、实对称矩阵、Hermite矩阵都是正规矩阵）

13、奇异矩阵：行列式为零的方阵，非奇异矩阵：行列式不为零的方阵，非奇异矩阵可以表示为若干个初等矩阵的乘积。

       可逆矩阵都是非奇异矩阵

14、正定矩阵：每个特征值都大于零

15、半正定矩阵：每个特征值大于或等于零

16、相似矩阵：设A，B为数域K上的两个n阶矩阵，如果存在K上的n阶非奇异矩阵P ，使得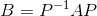,则称A相似于B，记为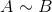

 

更新中...