机器学习高级-Chapter 04-概率论与贝叶斯分类

1 概率论

以下6个方面对概率论进行讲解
1.均匀分布
2.正态分布
3.数学期望
4.方差
5.标准差
6.多维随机变量及其分布

1.1 均匀分布

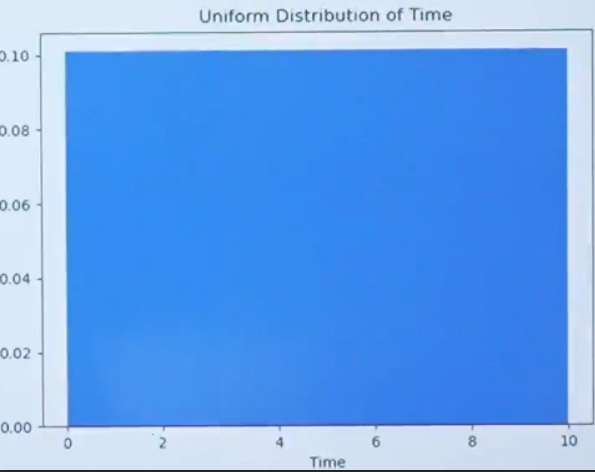
连续概率分布中最简单的均匀分布

假设某站的公交车每10min来一趟，那么乘客候车时间X是(0,10),这个X就是服从均匀分布的随机变量。

均匀分布的高度是一致的也就每一份概率是相同的。

均匀分布的概率密度函数形式为：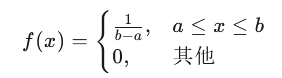

1.2 正态分布

正态分布（Normal distribution），又称高斯分布（Gaussian distribution），是统计学中最重要、最常见的连续型概率分布之一。

一、概率密度函数（PDF）

若随机变量 X 服从参数为 μ 和 σ2 的正态分布，记作：X∼N(μ,σ2)

则其概率密度函数为：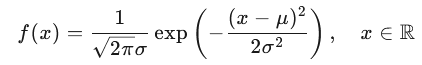

其中：

• μ：均值（mean），决定分布的中心位置

• σ：标准差（standard deviation），决定分布的“胖瘦”程度，σ>0

二、标准正态分布

当 μ=0、σ=1 时，称为标准正态分布：Z∼N(0,1)

其概率密度函数为：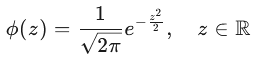

正态分布的引入

案例：在投硬币时，当投掷3次，“字”出现的次数会得到一个图像，如下所示：