1. K均值聚类理论讲解
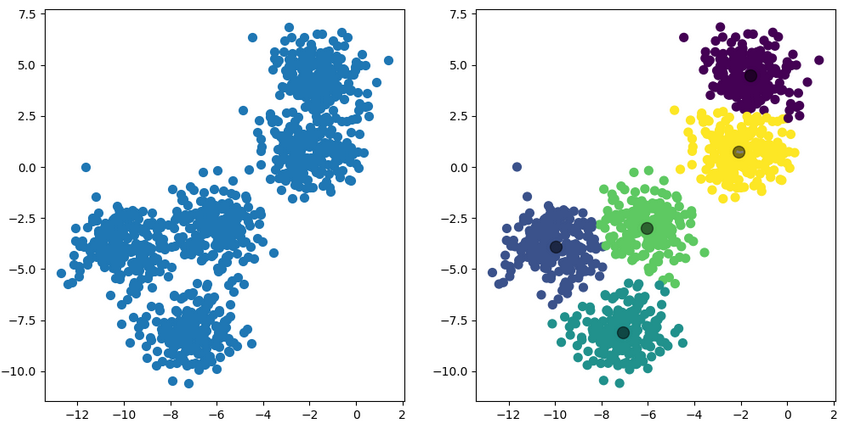
K均值聚类是一种常用的无监督学习算法,用于将数据集划分为K个不同的类型。其步骤如下:
1.随机选择原始数据的K个数据点作为初始质心(聚类中心)。
2.将每个数据点划分到距离最近的质心所对应的簇中,即计算每个数据点到每个质心的距离,选择距离最近的质心作为改数据点所属的簇。
3.重新计算每个簇的质心,即将该簇中所有数据点的坐标取平均值,得到新的质心。
4.重复低2步和第3步,直到簇内的数据点相似度达到一定程度,或者达到预设的最大迭代次数。
在K均值聚类算法中,相似度的计算通常采用欧氏距离或曼哈顿距离等距离度量方法。
同时,K均值聚类算法还有一些限制条件,例如质心的数量K需要事先确定,且算法对初始质心的选择比较敏感,不同的初始质心可能会导致不同的结果。
K均值聚类的目标是最小化簇内数据点与其所属聚类中心点的距离之和(即簇内误差平方和)。该算法通过迭代的方式不断优化聚类中心点的位置,使得簇内的数据点更加紧密地聚集在一起,而不同簇之间的距离更大。
代码运行步骤:
散点输入→设置聚类数目→开始迭代→数据点与聚类中心距离→更新聚类中心→绘制聚类结果
1.1 数据输入
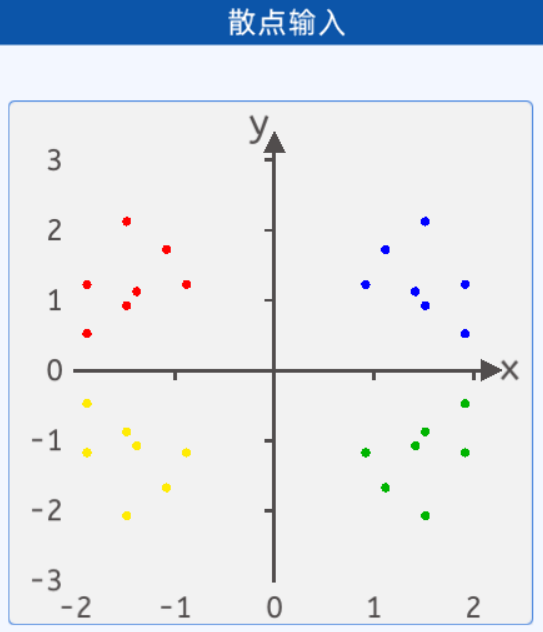
人为地输入数据,方便后期观察
蓝色点的坐标分别为:[1.9, 1.2],[1.5, 2.1],[1.9, 0.5],[1.5, 0.9],[0.9, 1.2],[1.1, 1.7],[1.4, 1.1]。
红色点的坐标分别为:[-1.9, 1.2],[-1.5, 2.1],[-1.9, 0.5],[-1.5, 0.9],[-0.9, 1.2],[-1.1, 1.7],[-1.4, 1.1]。
绿色点的坐标分别为:[1.9, -1.2],[1.5, -2.1],[1.9, -0.5],[1.5, -0.9],[0.9, -1.2],[1.1, -1.7],[1.4, -1.1]。
黄色点的坐标分别为:[-1.9, -1.2],[-1.5, -2.1],[-1.9, -0.5],[-1.5, -0.9],[-0.9, -1.2],[-1.1, -1.7],[-1.4, -1.1]。
1.2 设置聚类数目
根据K均值聚类算法的实现步骤,第一步需要随机选择K个数据点作为初始质心(聚类中心)。在“设置聚类数目”组件中可以设置K的值。

在开始时,随机选择k个数据点作为初始的聚类中心,或者从数据集中随机生成k个点作为初始中心。
1.3 开始迭代
该过程需要不断的计算聚类中心与各个点的距离,然后不断更新聚类中心,因此需要进行迭代。这里通过“开始迭代”组件设置迭代次数,与之前实验不同的是,本实验的迭代次数很小。
1.4 数据点与聚类中心距离
使用L2距离,即欧氏距离进行距离判别。
对于每个数据点,计算其与每个聚类中心的距离。将每个数据点分配给与其距离最近的聚类中心,形成k个簇(聚类),每个簇包含被分配到该聚类中心的数据点。
欧式距离和曼哈顿距离
欧氏距离是表征两点之间的直线距离,其在二维空间的计算公式为:
![]()
曼哈顿距离表示的是两点之间连线对各个坐标轴投影的长度总和,其示意图如下:
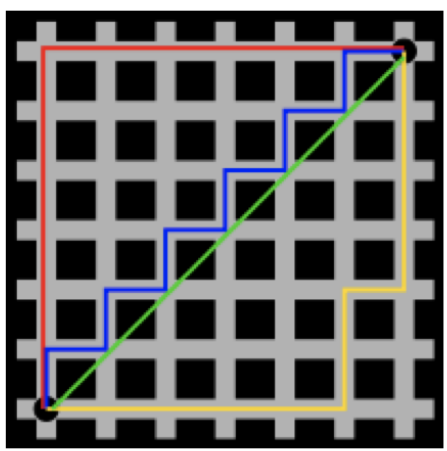
其中,红线、蓝线、黄线都是曼哈顿距离,绿线是欧氏距离。
曼哈顿距离计算公式为:![]()
1.5 更新聚类中心
对于每个簇,计算该簇内所有数据点在每个维度上的均值,得到新的聚类中心。新的聚类中心是该簇内所有数据点的平均位置,用于代表该簇的中心。
1.6 绘制聚类结果
一直更新聚类中心,把更新过程中聚类中心的点以及离它最近的点的连线绘制到图像上。

代码实现:
from sklearn.cluster import KMeans # 聚类算法
import numpy as np # 数组运算
import matplotlib.pyplot as plt # 画图
# 1.创建示例数据
class1_points = np.array([[1.9, 1.2],
[1.5, 2.1],
[1.9, 0.5],
[1.5, 0.9],
[0.9, 1.2],
[1.1, 1.7],
[1.4, 1.1]])
class2_points = np.array([[-1.9, 1.2],
[-1.5, 2.1],
[-1.9, 0.5],
[-1.5, 0.9],
[-0.9, 1.2],
[-1.1, 1.7],
[-1.4, 1.1]])
class3_points = np.array([[1.9, -1.2],
[1.5, -2.1],
[1.9, -0.5],
[1.5, -0.9],
[0.9, -1.2],
[1.1, -1.7],
[1.4, -1.1]])
class4_points = np.array([[-1.9, -1.2],
[-1.5, -2.1],
[-1.9, -0.5],
[-1.5, -0.9],
[-0.9, -1.2],
[-1.1, -1.7],
[-1.4, -1.1]])
"""
每个变量都是 7×2 的二维数组:7 个点,每个点 (x,y)。
4 组数据刚好在 4 个象限,方便肉眼验证聚类效果。
"""
# 合并四类数据点
data = np.concatenate((class1_points,
class2_points,
class3_points,
class4_points), axis=0)
"""
np.concatenate:把多个数组“粘”成一个大数组。
axis=0:按“行”方向粘,最后得到 28×2 的大数组 data。
"""
# 2.设置聚类簇数
k = 4
# 3.创建 KMeans 模型对象
km = KMeans(n_clusters=k, max_iter=30)
"""
| 参数 | 含义 |
| ------------- | ---------------- |
| n_clusters=k | 最终要得到 3 个簇(簇心) |
| max_iter=30 | 最多迭代 30 次,防止算太久 |
这一步只是创建空模型,里面没有任何数据。
"""
# 4.模型训练
km.fit(data) # 把数据传入
"""
内部流程:
随机选 4 个初始簇心 →
把 28 个点按“最近簇心”贴标签 →
重新计算簇心 →
重复 2-3 直到收敛(或 30 次上限)。
训练完成后,模型里就存好了最终簇心。
"""
# 获取最终簇心坐标
centroids = km.cluster_centers_
# 属性 .cluster_centers_ 是一个 3×2 的数组:第 i 行就是第 i 簇的“几何中心”(x, y)。
# 为什么是3×2的数组,应为输入特征为两列(x1,x2),k=3
# 给每个点打“簇标签”
y_kmean = km.predict(data)
"""
返回值 y_kmean 是一个 长度 28 的一维数组:
0、1、2、3,表示该点被分到哪一簇。
其实 .fit() 时已经算过一次,这里再 .predict() 只是演示用法
"""
# 打印标签
print(y_kmean)
# [3 3 3 3 3 3 3 2 2 2 2 2 2 2 0 0 0 0 0 0 0 1 1 1 1 1 1 1]
# 准备画布:左右两张子图
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 6))
"""
1 行 2 列 → 左边原始图,右边聚类图。
figsize=(12,6) 单位是英寸,宽 12 高 6。
"""
# 左图:原始散点(无颜色)
ax1.scatter(data[:, 0], data[:, 1], s=50)
"""
data[:, 0] 所有行的第 0 列 → x 坐标
data[:, 1] 所有行的第 1 列 → y 坐标
s=50 点的大小 50 像素
没有给颜色 → 统一默认蓝色,肉眼看到 4 团点。
"""
# 右图:把点按簇染色 + 画“虚线”连到簇心
for i in range(k): # i = 0,1,2
cluster_points = data[y_kmean == i] # 选出当前簇的所有点
centroid = centroids[i] # 当前簇心
for cluster_point in cluster_points: # 每个点到簇心画一条虚线
ax2.plot([cluster_point[0], centroid[0]],
[cluster_point[1], centroid[1]], 'k--')
# 'k--':黑色虚线 (k=black, --=dashed)。这样一眼能看出“谁归谁”
# 右图:再画一次散点,这次按簇上色
ax2.scatter(data[:, 0], data[:, 1], c=y_kmean, s=50)
"""
c=y_kmean:把标签当颜色 → 0/1/2/3 自动映射成四种颜色。
同一簇的点颜色相同。
"""
# 右图:把簇心画成大黑点
ax2.scatter(centroids[:, 0], centroids[:, 1],
c='black', s=100, alpha=0.5)
"""
s = 100
比前面大,突出簇心。
alpha = 0.5
半透明,防止遮挡。
"""
plt.savefig('K.png')
plt.show()
concat 粘数据,fit 学中心,predict 贴标签,scatter 画颜色,plot 画虚线,黑色大点就是心
代码运行结果:K.png
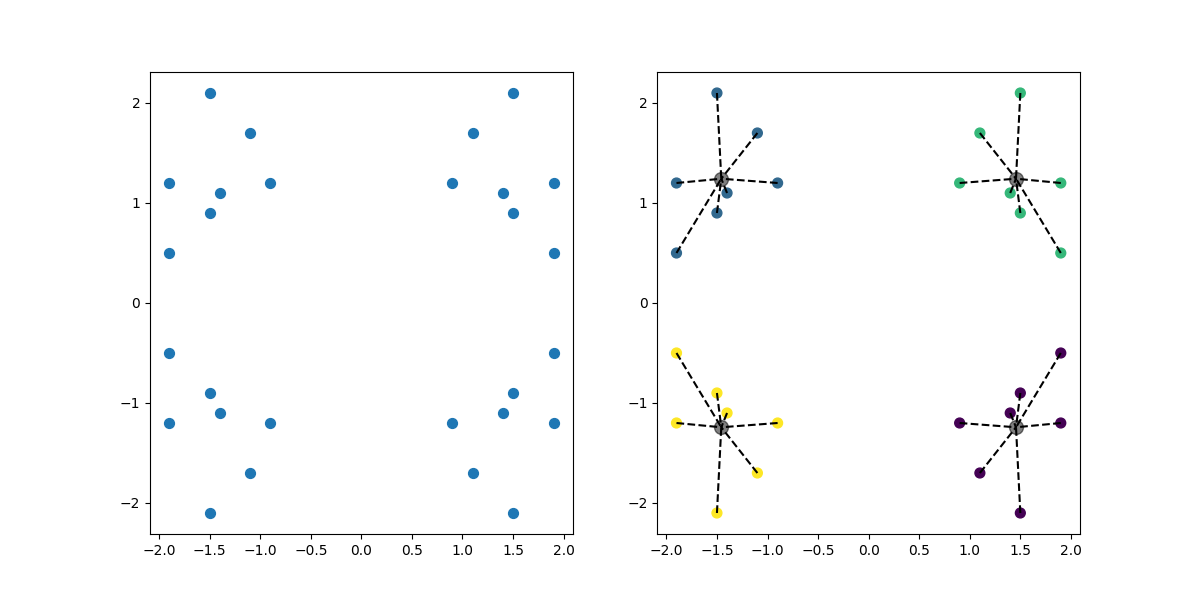
若把k值进行更换,例如改为3,分布不均匀每次运行代码会随机分为三份,效果如下:
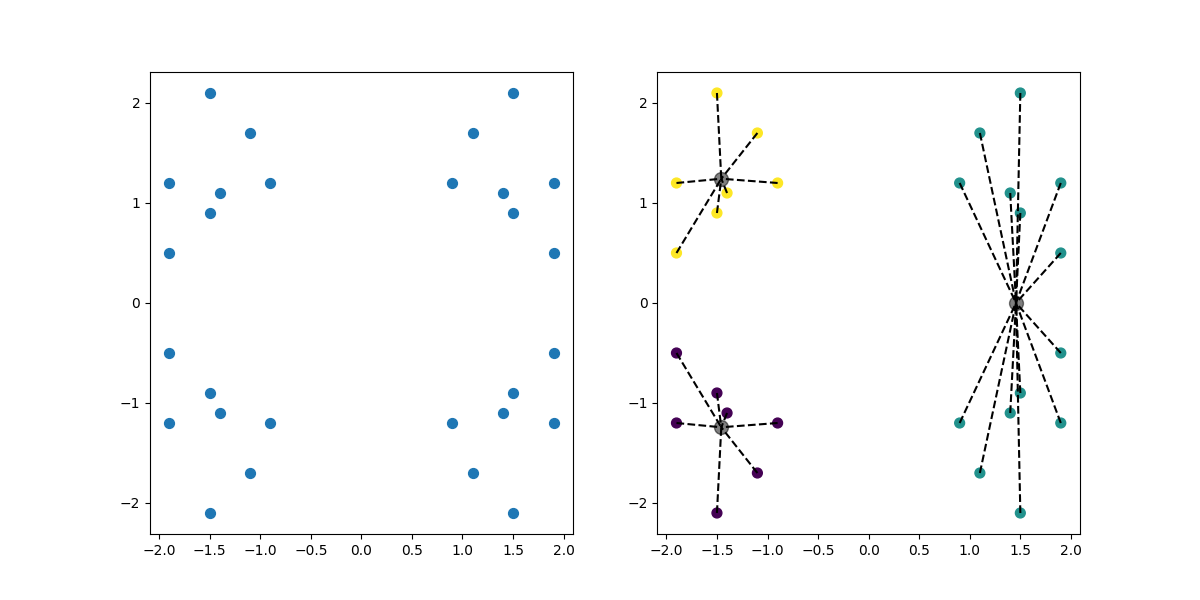
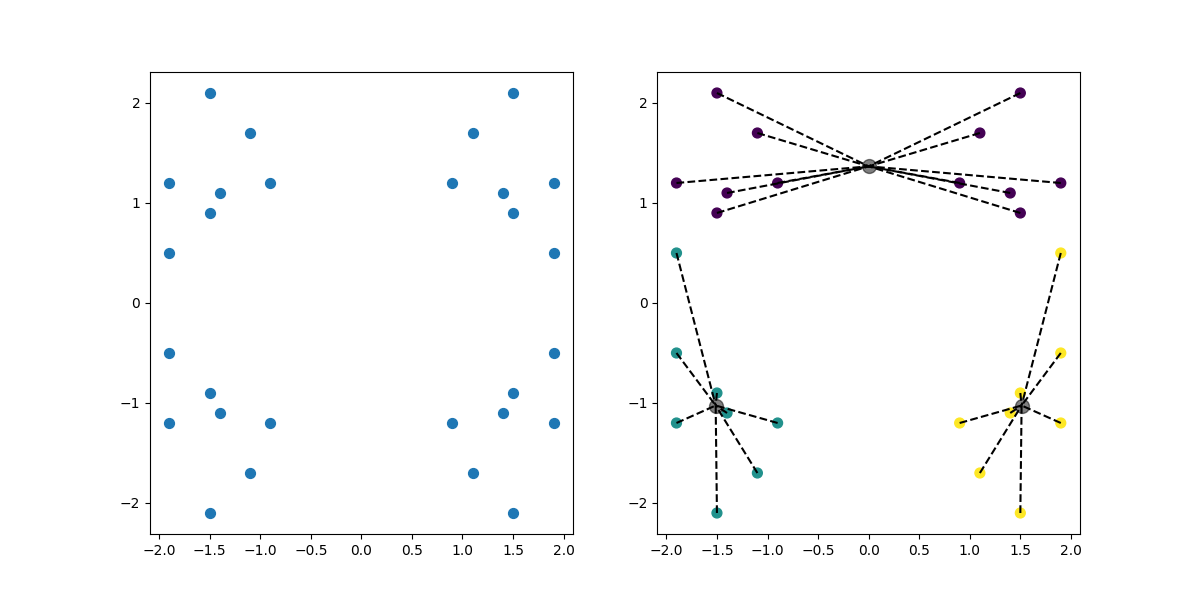





















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








