机器学习高级-Chapter 01-曲线拟合

从以下2个方面对曲线拟合进行介绍
        1.曲线拟合算法理论讲解
        2.编程实例与步骤
上面这2方面的内容，让大家，掌握并理解曲线拟合算法。

曲线拟合流程：

散点输入→前向计算→Sigmoid函数引入→参数初始化→损失函数→开始迭代→反向传播→显示频率设置→梯度下降显示

1 曲线拟合理论讲解

案例引入

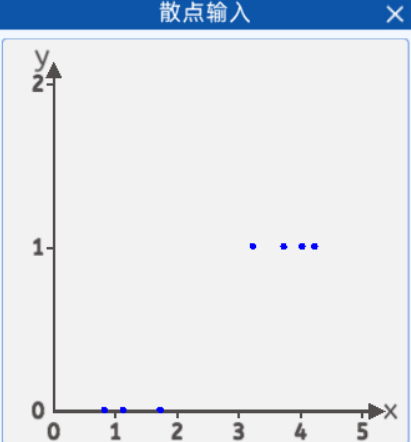
1.1 散点输入

本实验中，采集了天数与是否觅食的的关系数据，x轴表示天数，y轴表示是否觅食，0表示不需要觅食，1表示需要觅食，从图上看有3只蝌蚪是不需要觅食的，3天以下的不需要觅食。有4只需要觅食，大于3天的需要觅食。并且将它们绘制在一个二维坐标中，其分布如下图所示：

坐标分别为[0.8, 0]，[1.1, 0] ，[1.7, 0] ，[3.2, 1] ，[3.7, 1] ，[4.0, 1] ，[4.2, 1]。

1.2 前向计算

我们的目的是拟合这些散点，通过前向计算，我们通过修改w和b只能部分点落在线上，从实验看直线无法拟合这些点。

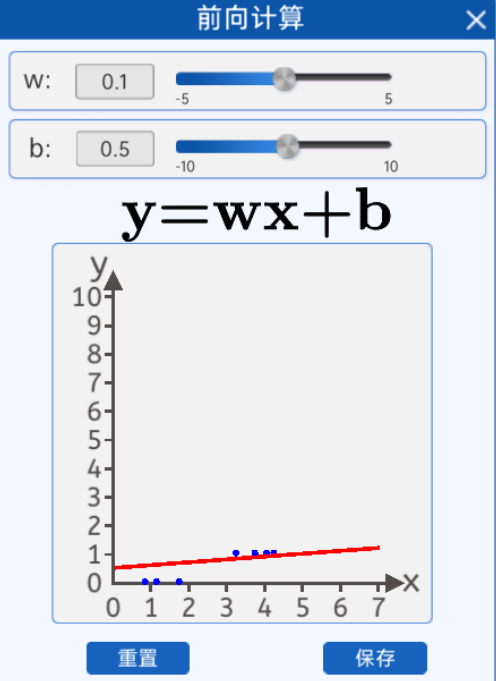
直线无法拟合那应该怎么办呢？

对于直线无法拟合这些点，是不是需要将直线变成曲线来拟合这些散点，在没有引入直线变曲线之前，使用直线是无法拟合这些点的。

看到这个图，我们想着可以使用分段函数

这个σ是一个激活函数。如果σ是阶跃函数，

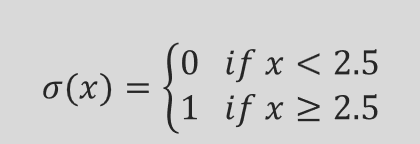
阶跃函数存在的问题？

        不连续性：在x=2.5处不连续；

        不可导性：在x=2.5处不存在导数；

怎么解决阶跃函数存在的问题呢？

我们是不是得找一个函数它要处处可微，是连续的，在各个地方都可导的，是不是就能很好的拟合当前曲线了。

阶跃函数可以作为激活函数吗？

阶跃函数（Step Function）可以作为激活函数，但在实际应用中并不常用。它的特点是：

定义：阶跃函数在某个阈值以下输出 0，在阈值以上输出 1。例如：

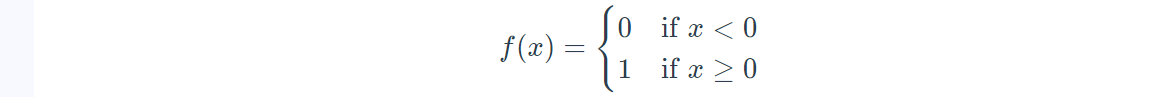
非连续性：阶跃函数是一个不连续的函数，这导致其在训练过程中无法计算梯度，因此不适合使用基于梯度的优化算法（如反向传播）。

局限性：由于其输出只有两种可能值，阶跃函数无法捕捉复杂的非线性关系，因此在深度学习中，通常选择如 ReLU、sigmoid 或 tanh 等激活函数，它们能够提供更平滑的梯度并支持更复杂的模型。

综上所述，尽管阶跃函数可以作为激活函数，但其缺乏梯度信息和灵活性使其在实际深度学习模型中不太适用。

1.3 Sigmoid函数引入

sigmoid拟合数据点效果图

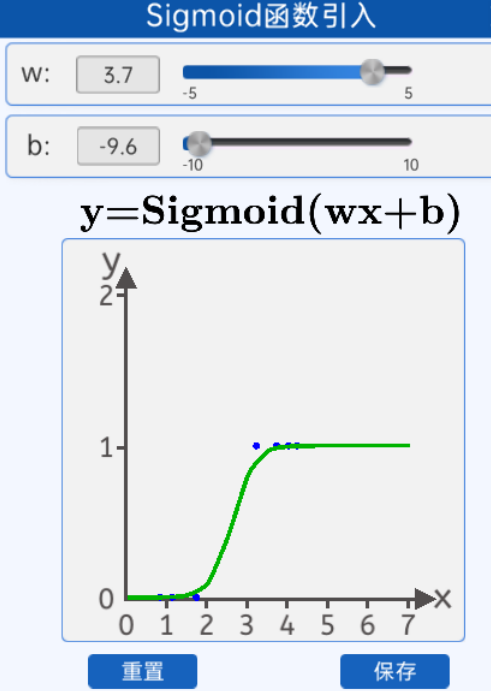
下面引入Sigmoid函数，当然是是前人慢慢发现的这个函数

Sigmoid的函数，其函数公式为：

其函数图像如下所示：

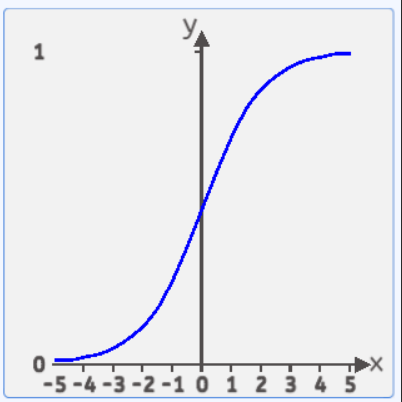
σ(x)的值域处于(0，1)之间，两边无限接近于0和1,但永远不等于0和1。定义域是负无穷到正无穷。

在线性回归中，直线的方程是，带入Sigmoid激活函数中，得到：

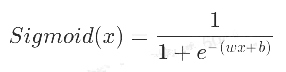
1.4 激活函数的引入

在该实验中，将直线转换成曲线，可以在直线 y=wx+b 加入一个新的函数 σ(wx+b) ，这个 σ 是一个激活函数，在上面实验中使用的激活函数是Sigmoid函数，当前还有其他激活函数，后面会讲。
激活函数是神经网络中一种重要的非线性函数，其作用在于引入非线性特性，使得神经网络能够学习和表示更加复杂的数据模式和关系。激活函数通常在每个神经元的输出上应用，将输入信号转换为输出信号。

以下是激活函数的主要作用：

1. 引入非线性特性：如果在神经网络中只使用线性变换，例如线性加权和求和，那么整个网络的组合效果将仍然是线性的。激活函数的非线性特性能够在每个神经元上引入非线性转换，从而让神经网络能够学习和表示更加复杂的函数和数据模式。

2. 提高模型的表达能力：激活函数的引入增加了神经网络的表达能力，使得网络可以逼近任何复杂的函数，这种特性称为“普遍逼近定理”（Universal Approximation Theorem）。

3. 稀疏性和稳定性：一些激活函数(如Relu)具有稀疏性和稳定性的特点，可以缓解梯度消失和梯度爆炸的问题，从而有助于训练更深的神经网络。

梯度消失简单解释：w新=w旧-学习率*梯度 (梯度为0，w新一直等于w旧，引起w不更新就是梯度消失)

梯度爆炸简单解释：w新=w旧-学习率*梯度 (梯度非常大 ，只要大于1，因为模型会有很多层，链式求导法则需要连乘，就会导致梯度爆炸。)

综上所述，激活函数在神经网络中扮演着非常重要的角色，它们的引入使得神经网络具备非线性表达能力，从而能够处理和解决更加复杂的任务。

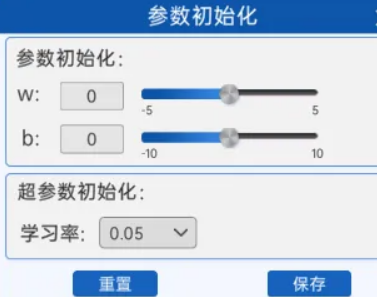
1.6 参数初始化

在之前的前向计算中，可以通过改变自己修改w和b来拟合这条曲线，但是在很多实际场景中，并没办法做到直接求出最优的w，b值，所以需要先随机定一个w和b，然后让梯度下降去拟合这些点。

在“参数初始化”组件中，可以初始化w和b的值以及学习率的值。

1.7 损失函数

根据公式：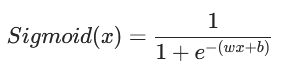

引入均方差损失函数中，于是损失函数就成了：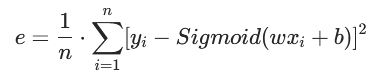

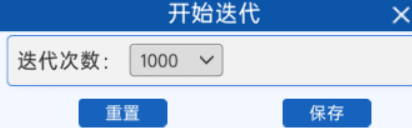
1.8 开始迭代

定义好损失函数后，选择好迭代次数，然后就可以进行反向传播了。

1.9 反向传播

在上面得到了损失函数的表达式，本实验中使用梯度下降的方式去降低损失函数值，于是需要对损失函数进行求导：

将其拆分成复合函数，得到：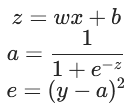

对复合函数求导，可得：

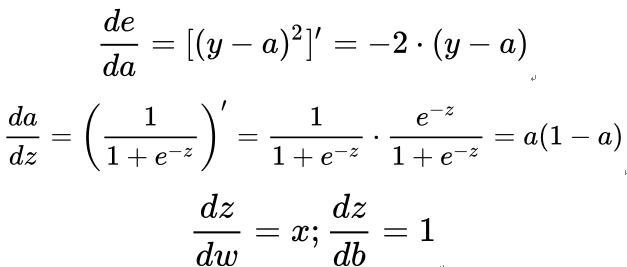
1.9 显示频率

通过设置显示频率，可以实时反馈当前的参数值和损失值。

1.10 梯度下降显示

通过可视化显示梯度下降

代码演示

# 1. 导入必要的库
import numpy as np  # Python中用于科学计算的核心库，提供高效的数组操作和数学函数
import matplotlib.pyplot as plt  # Python中常用的绘图库，用于数据可视化