Leetcode 437. 路径总和 III

最新推荐文章于 2025-12-20 20:19:18 发布

转载最新推荐文章于 2025-12-20 20:19:18 发布 · 175 阅读

0 ·

CC 4.0 BY-SA版权

原文链接：https://leetcode-cn.com/problems/path-sum-iii/solution/lu-jing-zong-he-iii-by-leetcode-solution-z9td/

文章标签：

#leetcode #算法

本文探讨了一种优化方法，通过前缀和和哈希表减少二叉树路径和问题的计算复杂度，从O(n^2)降低到O(n)。介绍了两种解法，包括深度优先搜索和利用前缀和的高效匹配。适合解决LeetCode中Path Sum III问题。

给定一个二叉树的根节点 root ，和一个整数 targetSum ，求该二叉树里节点值之和等于 targetSum 的路径的数目。

路径不需要从根节点开始，也不需要在叶子节点结束，但是路径方向必须是向下的（只能从父节点到子节点）。

示例 1：

输入：root = [10,5,-3,3,2,null,11,3,-2,null,1], targetSum = 8
输出：3
解释：和等于 8 的路径有 3 条，如图所示。
示例 2：

输入：root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22
输出：3

提示:

二叉树的节点个数的范围是 [0,1000]
-109 <= Node.val <= 109
-1000 <= targetSum <= 1000

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/path-sum-iii

解法一：

dfs, 以每个节点为起始点向下深度优先搜索。时间复杂度为O(n2), 空间复杂度为O(n)。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {

    int rootSum(TreeNode* root, int targetSum)//向下深度搜索
    {
        if(root==nullptr)return 0;
        int count=0;
        if(targetSum==root->val)count++; 
        count+=rootSum(root->left, targetSum-root->val);
        count+=rootSum(root->right, targetSum-root->val);    
        return count;
    }

public:
    int pathSum(TreeNode* root, int targetSum) {
        if(root==nullptr)return 0;
        int count=0;
        count+=rootSum(root, targetSum);//给定起始节点
        count+=pathSum(root->left,targetSum);//下一个起始节点
        count+=pathSum(root->right, targetSum);
        return count;
    }
};

解法二：

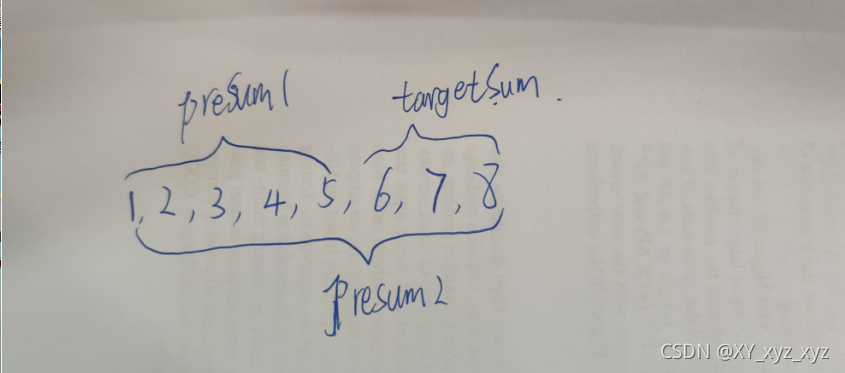
方法一中有许多节点被重复遍历，像这样求连续的和可以考虑使用前缀和。像这种题目经常用到二分查找，前缀和之类的。从根节点向下求前缀和，如root,r1,r2,r3,...,node这样一条路径，路径上的节点都有各自的前缀和，然后只需要在这些前缀和中匹配当前前缀和preSum减去targetSum，匹配过程可以用哈希表快速匹配。时间复杂度为与空间复杂度都为O(n)，

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
unordered_map<long long, int> preSum;

	int dfs(TreeNode* root, int targetSum, long long sum)
	{
		if (!root)return 0;
		int count = 0;
		sum += root->val;
		if (preSum[sum - targetSum] > 0)//与之前的匹配。
			count += preSum[sum - targetSum];
		preSum[sum]++;
		count+=dfs(root->left, targetSum, sum);
		count+=dfs(root->right, targetSum, sum);
		preSum[sum]--;
		return count;
	}

public:
	int pathSum(TreeNode* root, int targetSum) {
		preSum[0] = 1;
		return dfs(root, targetSum, 0);
	}
};