74.【必备】背包dp-多重背包、混合背包

原创

于 2025-07-27 20:40:58 发布 · 902 阅读

22 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #数据结构 #java

本文的网课内容学习自B站左程云老师的算法详解课程，旨在对其中的知识进行整理和分享~

网课链接：算法讲解075【必备】背包dp-多重背包、混合背包_哔哩哔哩_bilibili

一.多重背包模板

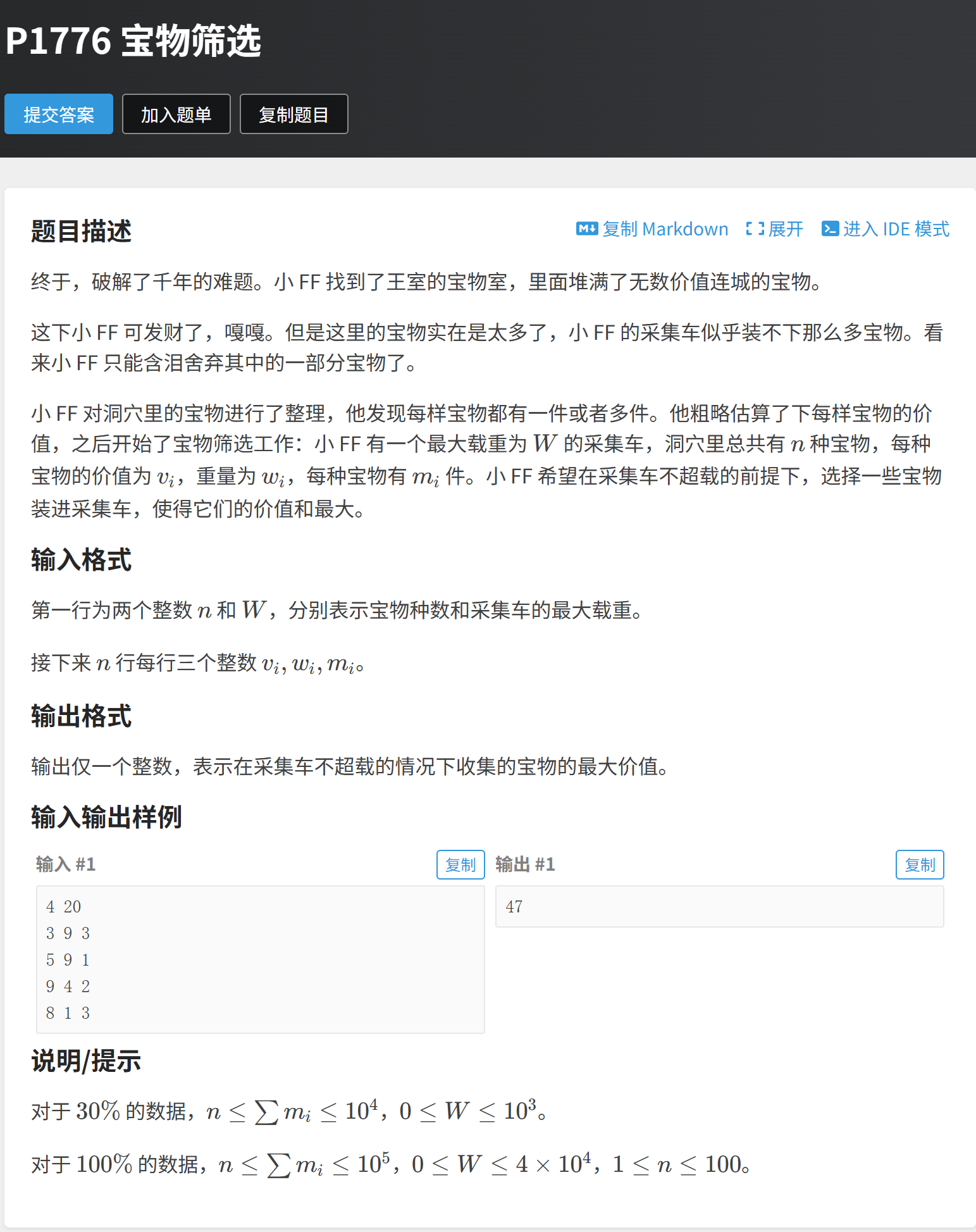
题目：P1776 宝物筛选

算法原理

整体原理
- 多重背包问题是背包问题的变种，其特点是每种物品有固定的数量限制（既不是无限取用，也不是只能取一次）。目标是在不超过背包容量的前提下，选择物品使得总价值最大。
- 问题特性：
  - 每种物品有重量 w[i]、价值 v[i] 和数量 c[i]。
  - 需要决定每种物品选取多少个（0到 c[i] 之间）。
- 动态规划定义：
  - dp[i][j] 表示考虑前 i 种物品时，背包容量为 j 时的最大价值。
  - 初始时，dp[j] = 0（没有物品时价值为0）。
- 状态转移：
  - 对于每种物品 i，遍历所有可能的背包容量 j（从0到 t）：
    - 初始时，dp[i][j] = dp[i-1][j]（不选当前物品）。
    - 枚举选取当前物品的数量 k（从1到 c[i]，且 k * w[i] <= j）：
      - 更新 dp[i][j] 为： dp[i][j] = Math.max(dp[i][j], dp[i-1][j - k * w[i]] + k * v[i]);

具体步骤

输入处理：
- 读取物品种类 n 和背包容量 t。
- 读取每种物品的价值 v[i]、重量 w[i] 和数量 c[i]。
初始化：
- 二维数组 dp 初始化为 dp[j] = 0。
动态规划填充：
- 对于每种物品 i：
  - 对于每个容量 j：
    - 初始化为不选当前物品的值 dp[i-1][j]。
    - 枚举选取数量 k，更新 dp[i][j]。
空间优化：
- 使用一维数组 dp[j]，逆序遍历 j 以避免覆盖之前的状态。
- 对于每种物品 i，从 t 到 0 遍历 j，并枚举 k。
结果提取：
- dp[n][t] 或 dp[t] 即为最大价值。
- 为什么需要逆序遍历？
  - 逆序确保在更新 dp[j] 时，dp[j - k * w[i]] 仍然是上一轮（i-1）的值，避免重复计算。
示例
- 假设 t = 5，物品：
  - 物品1：v=2，w=1，c=2。
  - 物品2：v=3，w=2，c=1。
- 动态规划过程：
  - 初始化 dp = [0, 0, 0, 0, 0, 0]。
  - 处理物品1：
    - j=5：可以选 k=1 或 k=2。
      - k=1：dp = max(0, dp + 2) = 2。
      - k=2：dp = max(2, dp + 4) = 4。
    - j=4：类似更新。
  - 处理物品2：
    - j=5：可以选 k=1。
      - dp = max(4, dp + 3) = 5。
  - 最终 dp = 5。
总结
- 通过动态规划枚举每种物品的选取数量，解决了多重背包问题。算法的时间复杂度为 O(n * t * c)（c 是平均数量），空间复杂度为 O(t)（优化后）。适用于物品种类和背包容量适中的场景。

代码实现

// 多重背包不进行枚举优化
// 宝物筛选
// 一共有n种货物, 背包容量为t
// 每种货物的价值(v[i])、重量(w[i])、数量(c[i])都给出
// 请返回选择货物不超过背包容量的情况下，能得到的最大的价值
// 测试链接 : https://www.luogu.com.cn/problem/P1776
// 请同学们务必参考如下代码中关于输入、输出的处理
// 这是输入输出处理效率很高的写法
// 提交以下的code，提交时请把类名改成"Main"，可以直接通过

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.io.PrintWriter;
import java.io.StreamTokenizer;

public class Code01_BoundedKnapsack {

    public static int MAXN = 101;

    public static int MAXW = 40001;

    public static int[] v = new int[MAXN];

    public static int[] w = new int[MAXN];

    public static int[] c = new int[MAXN];

    public static int[] dp = new int[MAXW];

    public static int n, t;

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StreamTokenizer in = new StreamTokenizer(br);
        PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));
        while (in.nextToken() != StreamTokenizer.TT_EOF) {
            n = (int) in.nval;
            in.nextToken();
            t = (int) in.nval;
            for (int i = 1; i <= n; i++) {
                in.nextToken(); v[i] = (int) in.nval;
                in.nextToken(); w[i] = (int) in.nval;
                in.nextToken(); c[i] = (int) in.nval;
            }
            out.println(compute2());
        }
        out.flush();
        out.close();
        br.close();
    }

    // 严格位置依赖的动态规划
    // 时间复杂度O(n * t * 每种商品的平均个数)
    public static int compute1() {
        // dp[0][....] = 0，表示没有货物的情况下，背包容量不管是多少，最大价值都是0
        int[][] dp = new int[n + 1][t + 1];
        for (int i = 1; i <= n; i++) {
            for (int j = 0; j <= t; j++) {
                dp[i][j] = dp[i - 1][j];
                for (int k = 1; k <= c[i] && w[i] * k <= j; k++) {
                    dp[i][j] = Math.max(dp[i][j], dp[i - 1][j - k * w[i]] + k * v[i]);
                }
            }
        }
        return dp[n][t];
    }

    // 空间压缩
    // 部分测试用例超时
    // 因为没有优化枚举
    // 时间复杂度O(n * t * 每种商品的平均个数)
    public static int compute2() {
        for (int i = 1; i <= n; i++) {
            for (int j = t; j >= 0; j--) {
                for (int k = 1; k <= c[i] && w[i] * k <= j; k++) {
                    dp[j] = Math.max(dp[j], dp[j - k * w[i]] + k * v[i]);
                }
            }
        }
        return dp[t];
    }

}

二.多重背包二进制分组优化

题目：P1776 宝物筛选

算法原理

整体原理
- 多重背包问题是背包问题的一个变种，其中每种物品有一定的数量限制（即每种物品可以选择多次，但不超过给定的数量）。这与完全背包问题（每种物品无限）和01背包问题（每种物品只有一个）不同。
- 二进制分组优化原理
  - 直接处理多重背包问题的一个简单方法是将每种物品拆分成多个独立的物品，然后使用01背包的方法解决。例如，如果一个物品有12个，可以将其拆分成12个相同的物品。然而，这种方法在物品数量较大时效率很低。
  - 二进制分组优化通过将物品的数量拆分成若干个2的幂次方的和，从而减少需要处理的物品数量。具体来说，对于数量为 cc 的物品，可以将其拆分成 1,2,4,…,2k,c−(2k+1−1)的组合。这样，任何数量的物品都可以通过这些组合的和来表示，同时物品的总数从 c 减少到 log⁡