73.【必备】背包dp-分组背包、完全背包

原创

于 2025-07-26 20:07:12 发布 · 815 阅读

9 ·

CC 4.0 BY-SA版权

文章标签：

#java #数据结构 #算法

本文的网课内容学习自B站左程云老师的算法详解课程，旨在对其中的知识进行整理和分享~

网课链接：算法讲解074【必备】背包dp-分组背包、完全背包_哔哩哔哩_bilibili

一.分组背包模板

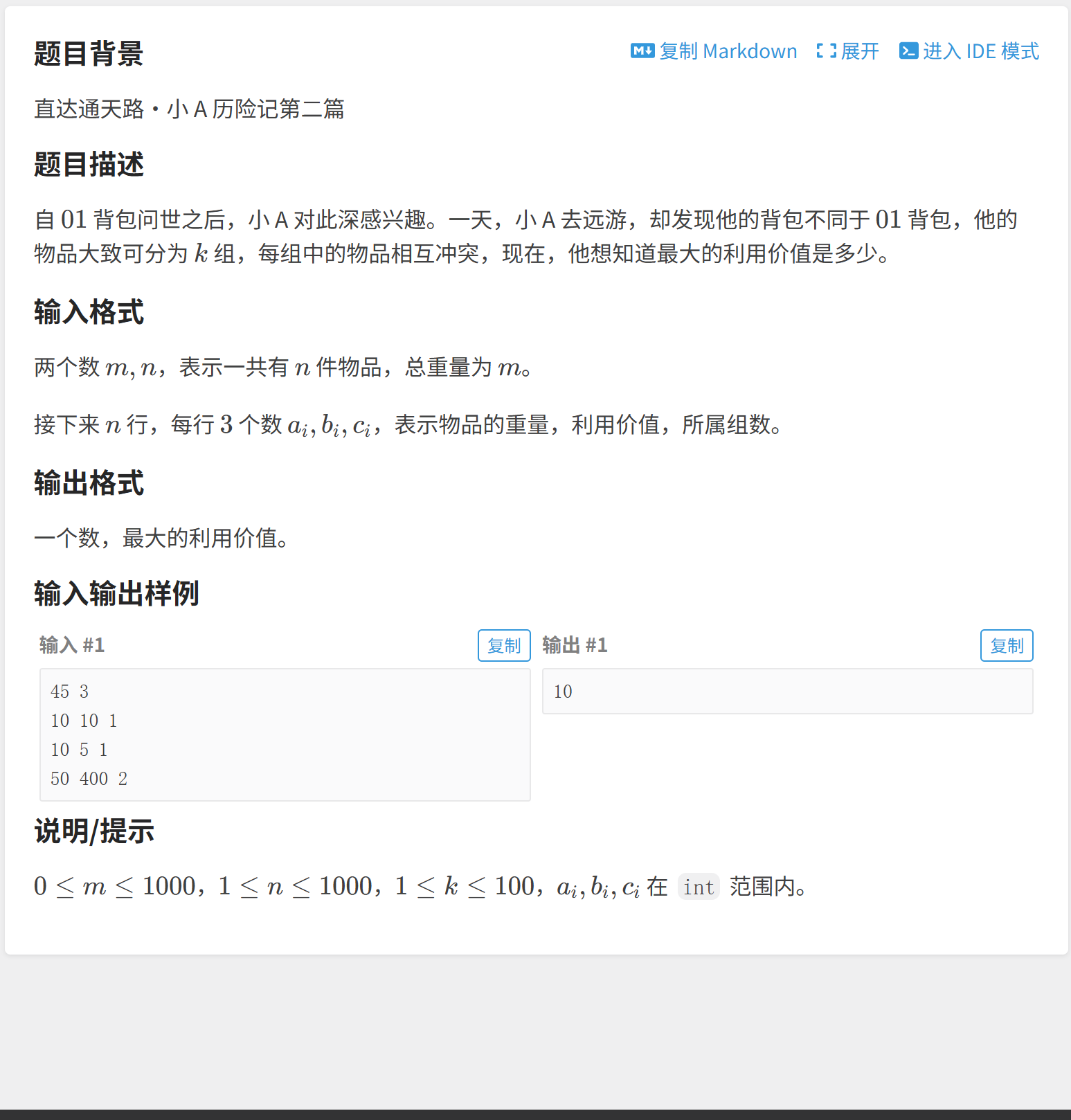
题目：P1757 通天之分组背包

算法原理

整体原理
- 分组背包问题是背包问题的一个变种，其特点是物品被分为若干组，每组中的物品只能选择一件或不选。目标是在不超过背包容量的前提下，选择物品使得总价值最大。
- 与传统的01背包问题不同，分组背包问题需要在每组中进行决策，而不是对每个物品单独决策。因此，动态规划的状态转移需要考虑组内的所有物品。
具体步骤
- 输入处理与初始化：
  - 读取背包容量 m 和物品数量 n。
  - 读取每个物品的体积、价值和组号，存储在数组 arr 中。
  - 按组号对物品进行排序，以便后续处理。
- 动态规划数组定义：
  - 定义 dp[i][j] 表示前 i 组物品，在容量不超过 j 时的最大价值。
  - 初始化 dp[j] = 0，表示前 0 组物品的价值为 0。
- 分组处理：
  - 遍历每一组物品，确定每组的起始和结束索引。
  - 对于每一组，遍历所有可能的背包容量 j（从 0 到 m）：
    - 初始时，dp[i][j] 继承自 dp[i-1][j]（即不选当前组的任何物品）。
    - 遍历当前组内的每一个物品，如果物品的体积不超过剩余容量 j，则更新 dp[i][j] 为：dp[i][j] = Math.max(dp[i][j], dp[i-1][j - arr[k][0]] + arr[k][1]);
- 空间优化：
  - 使用一维数组 dp[j] 代替二维数组，节省空间。
  - 在遍历容量 j 时，从大到小更新，避免覆盖之前的状态。
- 结果输出：
  - 最终结果存储在 dp[teams][m] 或 dp[m] 中，表示前 teams 组物品在容量 m 下的最大价值。
关键点
- 组内决策：每组只能选一个物品或不选，因此需要在组内遍历所有物品。
- 动态规划状态转移：状态转移时，需要比较不选当前组物品和选当前组某个物品的价值。
- 空间优化：通过逆序遍历容量，可以将二维动态规划优化为一维，减少空间复杂度。
- 这种方法确保了在分组约束下的最优解，同时通过动态规划高效地计算出最大价值。

代码实现

// 分组背包(模版)
// 给定一个正数m表示背包的容量，有n个货物可供挑选
// 每个货物有自己的体积(容量消耗)、价值(获得收益)、组号(分组)
// 同一个组的物品只能挑选1件，所有挑选物品的体积总和不能超过背包容量
// 怎么挑选货物能达到价值最大，返回最大的价值
// 测试链接 : https://www.luogu.com.cn/problem/P1757
// 请同学们务必参考如下代码中关于输入、输出的处理
// 这是输入输出处理效率很高的写法
// 提交以下的所有代码，并把主类名改成"Main"，可以直接通过

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.io.PrintWriter;
import java.io.StreamTokenizer;
import java.util.Arrays;

public class Code01_PartitionedKnapsack {

    public static int MAXN = 1001;

    public static int MAXM = 1001;

    // arr[i][0] i号物品的体积
    // arr[i][1] i号物品的价值
    // arr[i][2] i号物品的组号
    public static int[][] arr = new int[MAXN][3];

    public static int[] dp = new int[MAXM];

    public static int m, n;

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StreamTokenizer in = new StreamTokenizer(br);
        PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));
        while (in.nextToken() != StreamTokenizer.TT_EOF) {
            m = (int) in.nval;
            in.nextToken();
            n = (int) in.nval;
            for (int i = 1; i <= n; i++) {
                in.nextToken();
                arr[i][0] = (int) in.nval;
                in.nextToken();
                arr[i][1] = (int) in.nval;
                in.nextToken();
                arr[i][2] = (int) in.nval;
            }
            Arrays.sort(arr, 1, n + 1, (a, b) -> a[2] - b[2]);
            out.println(compute1());
        }
        out.flush();
        out.close();
        br.close();
    }

    // 严格位置依赖的动态规划
    public static int compute1() {
        int teams = 1;
        for (int i = 2; i <= n; i++) {
            if (arr[i - 1][2] != arr[i][2]) {
                teams++;
            }
        }
        // 组的编号1~teams
        // dp[i][j] : 1~i是组的范围，每个组的物品挑一件，容量不超过j的情况下，最大收益
        int[][] dp = new int[teams + 1][m + 1];
        // dp[0][....] = 0
        for (int start = 1, end = 2, i = 1; start <= n; i++) {
            while (end <= n && arr[end][2] == arr[start][2]) {
                end++;
            }
            // start ... end-1 -> i组
            for (int j = 0; j <= m; j++) {
                // arr[start...end-1]是当前组，组号一样
                // 其中的每一件商品枚举一遍
                dp[i][j] = dp[i - 1][j];
                for (int k = start; k < end; k++) {
                    // k是组内的一个商品编号
                    if (j - arr[k][0] >= 0) {
                        dp[i][j] = Math.max(dp[i][j], dp[i - 1][j - arr[k][0]] + arr[k][1]);
                    }
                }
            }
            // start去往下一组的第一个物品
            // 继续处理剩下的组
            start = end++;
        }
        return dp[teams][m];
    }

    // 空间压缩
    public static int compute2() {
        // dp[0][...] = 0
        Arrays.fill(dp, 0, m + 1, 0);
        for (int start = 1, end = 2; start <= n;) {
            while (end <= n && arr[end][2] == arr[start][2]) {
                end++;
            }
            // start....end-1
            for (int j = m; j >= 0; j--) {
                for (int k = start; k < end; k++) {
                    if (j - arr[k][0] >= 0) {
                        dp[j] = Math.max(dp[j], arr[k][1] + dp[j - arr[k][0]]);
                    }
                }
            }
            start = end++;
        }
        return dp[m];
    }

}

二.从栈中取出 K 个硬币的最大面值和

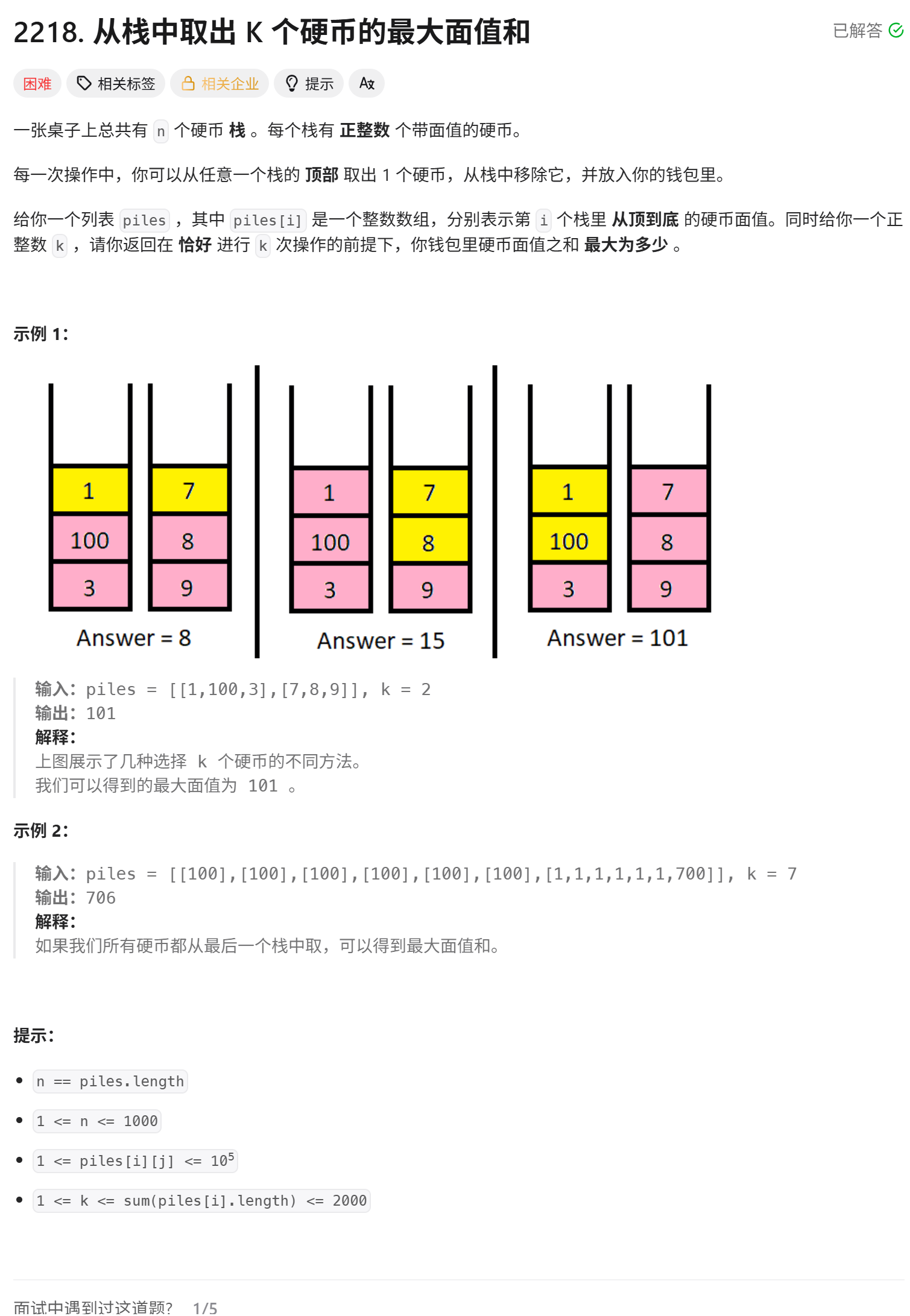
题目：从栈中取出 K 个硬币的最大面值和

算法原理

整体原理
- 该问题属于分组背包问题的变种，其中每个栈（组）中的硬币只能从顶部开始依次取出。目标是在恰好进行 k 次操作的前提下，获得最大的硬币面值总和。
- 分组背包特性：每组（栈）只能选择前 t 个硬币中的某个数量（t 是该栈的硬币数），且每组的选择会影响后续的选择。
- 动态规划：使用动态规划来记录在考虑前 i 组时，进行 j 次操作能获得的最大面值和。
具体步骤
- 输入处理：
  - piles 是多个栈的列表，每个栈包含若干硬币面值。
  - m 是操作次数（即背包容量）。
- 动态规划数组定义：
  - dp[i][j] 表示考虑前 i 组（栈）时，进行 j 次操作能获得的最大面值和。
  - 初始化 dp[j] = 0，表示前 0 组时无法获得任何面值。
- 预处理前缀和：
  - 对每个栈（组），计算其前 k 个硬币的面值累加和 preSum[k]，用于快速计算取 k 个硬币的总价值。
- 状态转移：
  - 不选当前组的硬币：dp[i][j] = dp[i-1][j]。
  - 选当前组的硬币：
    - 枚举当前组可能取的硬币数量 k（1 ≤ k ≤ min(t, j)），其中 t 是该组的硬币数。
    - 更新 dp[i][j] 为：dp[i][j] = Math.max(dp[i][j], dp[i-1][j - k] + preSum[k]);
    - 表示在剩余 `j - k` 次操作中从前 `i-1` 组取硬币，加上当前组取 `k` 个硬币的面值和。